1 2 Divided By 5
wordexpert
Sep 11, 2025 · 6 min read
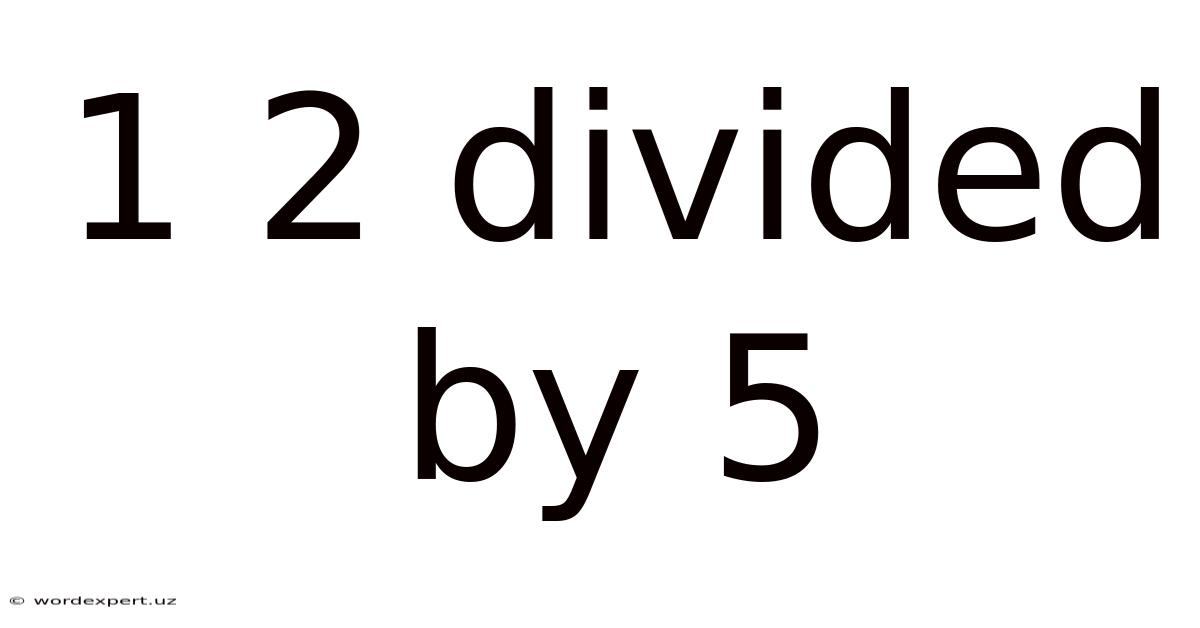
Table of Contents
Unveiling the Mystery: A Deep Dive into 12 Divided by 5
The seemingly simple question, "What is 12 divided by 5?", opens a door to a fascinating world of mathematical concepts. While the answer might seem straightforward at first glance, a deeper exploration reveals underlying principles that are fundamental to arithmetic, algebra, and even more advanced mathematical fields. This comprehensive guide will not only provide the answer but also delve into the methodology, different ways to represent the solution, and the broader mathematical significance of division.
Understanding Division: The Foundation
Division is one of the four fundamental arithmetic operations, alongside addition, subtraction, and multiplication. It essentially involves splitting a quantity into equal parts. In the context of "12 divided by 5," we're asking: "How many times does 5 fit into 12?" This seemingly simple question lays the groundwork for understanding more complex divisions and fractional concepts.
Method 1: Long Division – The Classic Approach
Long division is a time-tested method for solving division problems, especially those involving larger numbers. Let's apply it to 12 divided by 5:
-
Set up the problem: Write 12 inside the long division symbol (⟌) and 5 outside.
-
Determine the quotient: Ask yourself, "How many times does 5 go into 12?" The answer is 2. Write the 2 above the 12.
-
Multiply: Multiply the quotient (2) by the divisor (5): 2 x 5 = 10. Write this 10 below the 12.
-
Subtract: Subtract the result (10) from the dividend (12): 12 - 10 = 2. This is the remainder.
-
Express the result: The result of 12 divided by 5 is 2 with a remainder of 2. This can be written as: 12 ÷ 5 = 2 R 2
Method 2: Decimal Representation – Moving Beyond Remainders
The remainder method is perfectly acceptable for many applications. However, representing the answer as a decimal provides a more complete and often more useful result in various contexts. To convert the remainder into a decimal, we continue the long division process:
-
Add a decimal point: Add a decimal point to the dividend (12) and add a zero. This doesn't change the value of the number, it just allows us to continue the division. Now we have 12.0.
-
Bring down the zero: Bring down the zero next to the remainder 2, making it 20.
-
Divide: Ask, "How many times does 5 go into 20?" The answer is 4. Write the 4 after the decimal point in the quotient.
-
Multiply and Subtract: Multiply 4 by 5 (20) and subtract it from 20, resulting in a remainder of 0.
-
Final Answer: The final answer is 2.4. Therefore, 12 ÷ 5 = 2.4
Method 3: Fractions – Representing Parts of a Whole
Fractions offer another elegant way to represent the solution to 12 divided by 5. A fraction represents a part of a whole, where the top number (numerator) is the part and the bottom number (denominator) is the whole.
-
Express as a fraction: The division problem "12 divided by 5" can be written as the fraction 12/5.
-
Simplify (if possible): In this case, the fraction 12/5 is already in its simplest form because 12 and 5 have no common factors other than 1.
-
Convert to a mixed number (optional): While 12/5 is perfectly valid, it's often helpful to express it as a mixed number – a whole number and a fraction. To do this, divide the numerator (12) by the denominator (5):
- 12 ÷ 5 = 2 with a remainder of 2.
- The whole number part is 2.
- The fractional part is the remainder (2) over the denominator (5), which is 2/5.
- So, 12/5 as a mixed number is 2 2/5.
Therefore, 12 divided by 5 can be represented as 12/5, or 2 2/5, both of which are equivalent to 2.4.
The Significance of Remainders and Decimals
The choice between a remainder and a decimal representation depends heavily on the context of the problem.
-
Remainders: Remainders are particularly useful when dealing with situations where fractional parts don't make sense. For example, if you have 12 apples and want to divide them equally among 5 people, each person gets 2 apples, and you have 2 apples left over. The remainder highlights the leftover quantity.
-
Decimals: Decimals are essential when dealing with measurements, quantities that can be subdivided infinitely (like money or weight), or when precision is required in calculations. For example, if you're dividing 12 meters of fabric into 5 equal pieces, each piece would be 2.4 meters long.
Applying the Concept: Real-World Examples
The concept of dividing 12 by 5 pops up in various real-world scenarios:
- Sharing resources: Distributing 12 cookies among 5 friends.
- Calculating unit prices: If 5 identical items cost $12, each item costs $2.40.
- Averaging: Finding the average score of 5 tests totaling 120 points.
- Measurement and scaling: Dividing a 12-inch long piece of wood into 5 equal segments.
Beyond the Basics: Exploring Advanced Concepts
The seemingly simple problem of 12 divided by 5 provides a springboard to explore more advanced mathematical concepts:
-
Modular Arithmetic: The remainder (2 in this case) is crucial in modular arithmetic, a system of arithmetic for integers where numbers "wrap around" upon reaching a certain value (the modulus). This has applications in cryptography and computer science.
-
Fractional Arithmetic: Understanding fractions is paramount in algebra, calculus, and many other advanced math disciplines. The ability to manipulate and simplify fractions is a foundational skill.
-
Decimal Expansions: Understanding decimal expansions (like 2.4) is crucial in understanding real numbers and their properties. Infinite decimal expansions lead to concepts like irrational numbers (like π and √2).
Frequently Asked Questions (FAQs)
Q: What is the most accurate way to express 12 divided by 5?
A: While 2 R 2 is perfectly valid, 2.4 is generally considered more precise for most applications involving continuous quantities or requiring decimal precision. The fractional representation, 12/5 or 2 2/5, also provides an exact representation. The "best" representation depends on the specific context.
Q: Can I use a calculator to solve this?
A: Absolutely! Calculators provide a quick and efficient way to solve division problems, especially with larger numbers.
Q: Why is understanding division important?
A: Division is a fundamental arithmetic operation used extensively in various fields, from everyday calculations to advanced scientific computations. A solid grasp of division is crucial for problem-solving in mathematics and other quantitative disciplines.
Conclusion: More Than Just an Answer
The seemingly simple question, "What is 12 divided by 5?", opens the door to a surprisingly rich world of mathematical concepts. The solution, whether expressed as 2 R 2, 2.4, 12/5, or 2 2/5, illustrates fundamental principles of arithmetic, laying the groundwork for understanding more complex mathematical ideas. Mastering the different approaches to solving division problems builds a strong mathematical foundation essential for success in various academic and professional pursuits. The journey from a simple division problem to a deeper understanding of its underlying principles highlights the beauty and interconnectedness of mathematics.
Latest Posts
Latest Posts
-
How To Find Triangle Height
Sep 11, 2025
-
Measurement Of A Graduated Cylinder
Sep 11, 2025
-
How Long Is 75 Weeks
Sep 11, 2025
-
1991 How Old Am I
Sep 11, 2025
-
Density Of Aluminum Lb In3
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 1 2 Divided By 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.