1 3 Of 8 Oz
wordexpert
Sep 22, 2025 · 5 min read
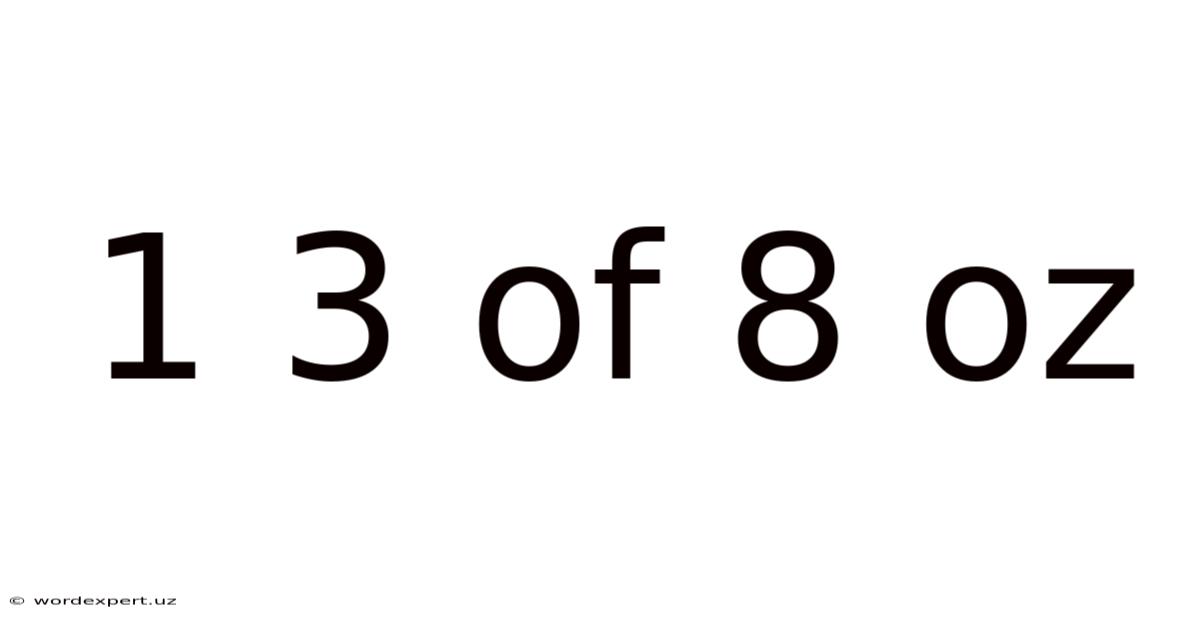
Table of Contents
Decoding the Mystery: Understanding "1 3 of 8 oz" and its Applications
Many find themselves grappling with fractional measurements, especially when dealing with recipes, scientific experiments, or even everyday tasks involving liquids. The phrase "1 3 of 8 oz" presents a seemingly simple yet potentially confusing calculation. This article aims to demystify this type of problem, explaining not only how to solve it but also expanding on the broader concept of fractions and their practical applications. We will delve into the calculation itself, discuss the underlying mathematical principles, explore different scenarios where such calculations are necessary, and provide a comprehensive understanding of this seemingly simple concept.
Understanding Fractions: A Quick Refresher
Before we tackle the specific problem, let's revisit the fundamentals of fractions. A fraction represents a part of a whole. It is expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator shows the total number of parts the whole is divided into. For example, in the fraction 1/2, the numerator is 1, and the denominator is 2, representing one out of two equal parts.
Breaking Down "1 3 of 8 oz"
The phrase "1 3 of 8 oz" translates to finding one-third (1/3) of 8 ounces. This is a simple fraction-of-a-quantity problem. To solve it, we need to perform a multiplication operation.
The Calculation: Step-by-Step
-
Convert the fraction to a decimal: The fraction 1/3 can be converted to a decimal by dividing the numerator (1) by the denominator (3). This gives us approximately 0.333 (the decimal representation of 1/3 is recurring, meaning it continues infinitely).
-
Multiply the decimal by the quantity: Now, multiply the decimal equivalent of 1/3 (approximately 0.333) by the quantity in ounces (8 oz). 0.333 * 8 oz ≈ 2.664 oz
-
Rounding (if necessary): Depending on the context, you might need to round the result to a more practical value. For example, if you're dealing with a recipe, rounding to 2.7 oz or even 2 ⅔ oz might be appropriate. If you’re dealing with a precise scientific measurement, however, you might need to retain more decimal places.
Therefore, 1/3 of 8 oz is approximately 2.664 oz.
Alternative Calculation Method: Using Fractions Directly
Instead of converting to decimals, we can solve this using fractions directly:
-
Rewrite the problem: We need to calculate (1/3) * 8 oz.
-
Express 8 as a fraction: We can express 8 as a fraction by writing it as 8/1.
-
Multiply the fractions: Now, multiply the two fractions: (1/3) * (8/1) = (18) / (31) = 8/3
-
Simplify or convert to a mixed number: The fraction 8/3 is an improper fraction (the numerator is larger than the denominator). We can convert it to a mixed number by dividing the numerator (8) by the denominator (3): 8 ÷ 3 = 2 with a remainder of 2. This means 8/3 is equal to 2 and 2/3. Therefore, 1/3 of 8 oz is 2 ⅔ oz.
This fractional representation (2 ⅔ oz) is often more accurate than the decimal approximation (2.664 oz), especially in situations where precise measurements are critical.
Practical Applications: Where This Calculation Matters
The ability to calculate fractions of quantities, like "1 3 of 8 oz," is surprisingly useful in many areas of life:
-
Cooking and Baking: Recipes often require fractional measurements of ingredients. Understanding how to calculate 1/3 of a cup of flour or 1/4 of a teaspoon of baking powder is essential for successful baking. This extends to scaling recipes up or down—a skill valuable for both home cooks and professional chefs.
-
Medicine and Healthcare: Dosage calculations are crucial in medicine. Nurses, pharmacists, and doctors frequently need to calculate fractional doses of medication to ensure patient safety and efficacy. Accurate calculation is critical to avoid both underdosing and potentially dangerous overdosing.
-
Science and Engineering: Many scientific experiments and engineering projects involve precise measurements. Calculating fractions of volumes, weights, or other quantities is fundamental in fields like chemistry, physics, and construction.
-
DIY Projects and Crafts: Whether building furniture, sewing clothes, or working on other DIY projects, precise measurements are vital for a successful outcome. Calculating fractions of inches or centimeters can be crucial to ensure accuracy.
-
Finance and Budgeting: Calculating percentages or fractions of budgets is important for personal finance management and business accounting. Understanding how to allocate resources proportionally is essential for financial planning.
Frequently Asked Questions (FAQ)
-
Q: What if I need to calculate a different fraction of 8 oz?
-
A: The process remains the same. Simply replace 1/3 with the desired fraction, and follow the steps outlined above. For example, to calculate 2/5 of 8 oz: (2/5) * 8 = 16/5 = 3 1/5 oz or approximately 3.2 oz.
-
Q: Is it always better to use fractions rather than decimals?
-
A: While fractions often offer greater accuracy, decimals are sometimes more convenient, particularly when dealing with more complex calculations or when a high degree of precision isn't crucial. Context dictates the best approach.
-
Q: Are there online tools or calculators to help with these calculations?
-
A: Yes, numerous online calculators are readily available to help with fractional calculations and conversions. These can be helpful for quick calculations, but understanding the underlying principles is crucial for problem-solving.
-
Q: What happens if the calculation results in a recurring decimal?
-
A: Recurring decimals often represent fractions. Sometimes, it's best to leave the answer in fractional form to maintain accuracy. In other contexts, rounding to a suitable level of precision might be necessary.
Conclusion: Mastering Fractional Calculations
Understanding how to solve problems like "1 3 of 8 oz" is not just about getting the right answer; it's about grasping the fundamental principles of fractions and their application in diverse fields. By mastering this seemingly simple calculation, you gain a valuable skill applicable across numerous disciplines, leading to improved accuracy and greater confidence in various aspects of life. The ability to seamlessly translate fractions into decimals and vice versa, along with the capacity to work with mixed numbers, will prove an asset in numerous practical scenarios. Remember, the key is understanding the process, not just memorizing the solution. The more you practice these calculations, the easier they become, solidifying your understanding of fractional mathematics.
Latest Posts
Latest Posts
-
How To Solve Ssa Triangle
Sep 23, 2025
-
90 Days From November 13
Sep 23, 2025
-
Density Of Air At 20c
Sep 23, 2025
-
100 Gramos Cuantas Onzas Son
Sep 23, 2025
-
90 Days From January 13
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 1 3 Of 8 Oz . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.