10 Out Of 12 Percentage
wordexpert
Sep 21, 2025 · 6 min read
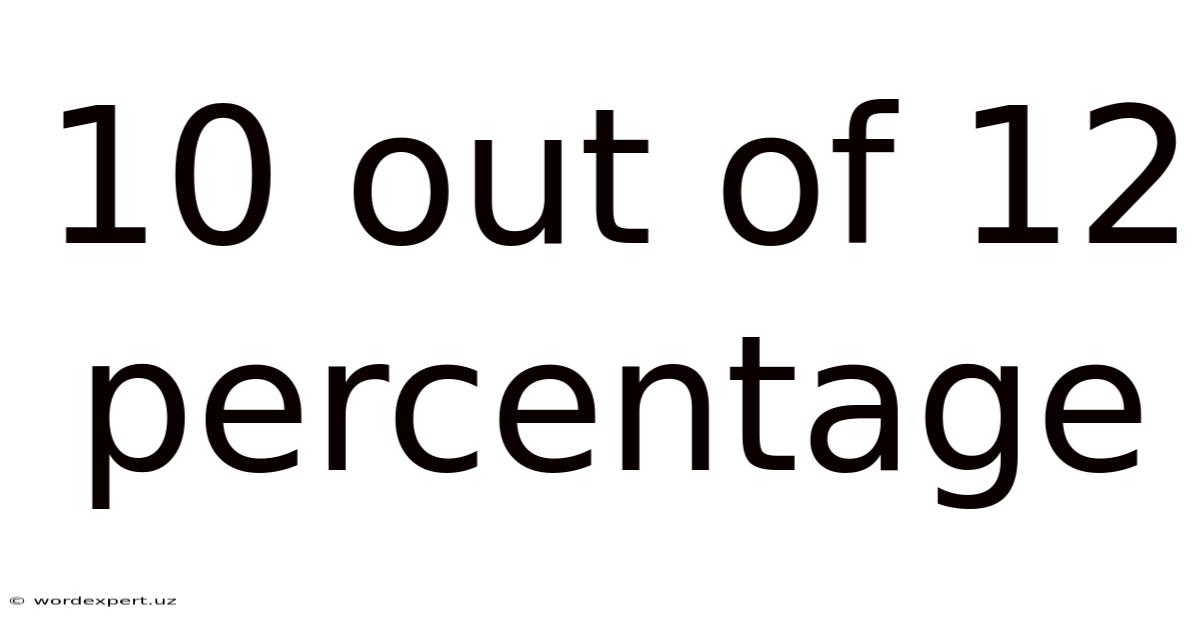
Table of Contents
Understanding 10 Out of 12: Percentages, Fractions, and Real-World Applications
Calculating percentages is a fundamental skill applicable across numerous fields, from academic assessments to financial planning. This article delves into the meaning of "10 out of 12," explaining its representation as a fraction, decimal, and percentage, along with various real-world examples and practical applications. We'll explore the underlying mathematical concepts and provide a step-by-step guide to understanding and calculating similar scenarios.
What Does "10 Out of 12" Mean?
The phrase "10 out of 12" signifies that out of a total of 12 items, 10 possess a specific characteristic or meet a certain criteria. It represents a part of a whole. This part-to-whole relationship is fundamental to understanding fractions, decimals, and percentages.
Representing 10 Out of 12 as a Fraction
The simplest way to represent "10 out of 12" is as a fraction: 10/12. This fraction indicates 10 parts out of a total of 12 equal parts. This fraction can be simplified by finding the greatest common divisor (GCD) of 10 and 12, which is 2. Dividing both the numerator (10) and the denominator (12) by 2, we get the simplified fraction 5/6. This means that 10 out of 12 is equivalent to 5 out of 6.
Converting the Fraction to a Decimal
To convert the fraction 5/6 to a decimal, we divide the numerator (5) by the denominator (6):
5 ÷ 6 = 0.8333...
The decimal representation is 0.8333..., which is a recurring decimal. For practical purposes, we often round this to a specific number of decimal places. For example, rounded to two decimal places, it becomes 0.83.
Calculating the Percentage
A percentage represents a fraction or decimal expressed as a part of 100. To convert the fraction 5/6 or the decimal 0.8333... to a percentage, we multiply by 100%:
(5/6) * 100% = 83.33...%
Rounding to two decimal places, we get 83.33%. Therefore, 10 out of 12 represents 83.33%.
Real-World Applications of Percentage Calculations
Understanding how to calculate percentages is crucial in many everyday situations:
-
Academic Performance: Imagine a student scores 10 out of 12 on a quiz. Their percentage score is 83.33%, providing a clear measure of their performance relative to the total possible marks. This allows for easy comparison with other students and tracking of progress over time.
-
Financial Calculations: Percentage calculations are fundamental in finance. Interest rates, discounts, tax rates, and profit margins are all expressed as percentages. For example, a 10% discount on a $100 item means a saving of $10. Understanding percentage changes is essential for analyzing investments and budgeting.
-
Data Analysis and Statistics: Percentages are extensively used to represent proportions within datasets. In surveys and polls, results are frequently presented as percentages to show the distribution of opinions or preferences within a population. For instance, if 10 out of 12 respondents prefer a certain product, that's an 83.33% preference rate.
-
Scientific Research: Percentages play a critical role in scientific studies, particularly when reporting experimental results. For example, if 10 out of 12 lab mice respond positively to a new drug, the success rate is 83.33%, providing valuable information about the drug's effectiveness.
-
Everyday Life: Many everyday situations involve percentage calculations, from calculating tips in restaurants to understanding sales tax, discounts in stores, and even determining the nutritional content of food.
Different Ways to Calculate Percentages
There are several approaches to calculate percentages, all leading to the same result. Here are some common methods:
Method 1: Using Fractions
- Express the situation as a fraction: Determine the part (10) and the whole (12). This gives the fraction 10/12.
- Simplify the fraction (if possible): Simplify 10/12 to 5/6.
- Convert the fraction to a decimal: Divide the numerator by the denominator (5 ÷ 6 = 0.8333...).
- Convert the decimal to a percentage: Multiply the decimal by 100% (0.8333... * 100% = 83.33%).
Method 2: Using Proportions
- Set up a proportion: Set up a proportion where x represents the percentage: 10/12 = x/100.
- Cross-multiply: Multiply 10 by 100 and 12 by x: 1000 = 12x.
- Solve for x: Divide both sides by 12: x = 1000/12 = 83.33...
- Express as a percentage: The result, 83.33..., represents the percentage.
Method 3: Using a Calculator
Most calculators have a percentage function. Simply divide the part (10) by the whole (12) and then multiply by 100.
Extending the Understanding: Variations and Applications
The principle of calculating "10 out of 12" can be extended to numerous scenarios:
-
Larger Numbers: The same principles apply to larger numbers. For example, if 100 out of 120 items meet a certain criterion, the percentage is still calculated by dividing the part (100) by the whole (120) and multiplying by 100%.
-
Different Units: The concept extends beyond numerical values. If 10 out of 12 students passed an exam, the pass rate is still 83.33%. The units change, but the underlying calculation remains the same.
-
Inverse Calculations: You can also work backward. If you know the percentage and the whole, you can calculate the part. For example, if 83.33% of students passed an exam and there were 12 students, you can calculate the number of students who passed.
Frequently Asked Questions (FAQ)
Q: What if I have a decimal number in the "out of" value?
A: The same principles apply. For example, if you have 10 out of 12.5, you would still divide 10 by 12.5 and multiply by 100 to get the percentage.
Q: Why do we use percentages?
A: Percentages provide a standardized way to compare proportions. They make it easier to understand and communicate data regardless of the absolute numbers involved.
Q: Are there any online tools to help calculate percentages?
A: Yes, numerous online percentage calculators are available that can simplify the calculation process.
Q: How do I handle rounding errors?
A: Rounding errors can occur when working with decimals. It's best to keep as many decimal places as possible during calculations and only round the final result to the desired level of precision.
Conclusion
Understanding how to calculate "10 out of 12" as a percentage is a valuable skill with broad applications in various aspects of life. This article has provided a detailed explanation of the process, covering fractions, decimals, percentages, and various practical applications. Mastering this skill empowers you to analyze data effectively, make informed decisions, and tackle numerous real-world challenges with confidence. Remember to practice regularly to solidify your understanding and build your proficiency in percentage calculations. The ability to understand and manipulate percentages is a cornerstone of numeracy and a skill that will serve you well throughout your life.
Latest Posts
Latest Posts
-
Whats 20 Of 200 000
Sep 21, 2025
-
6 Million Minutes In Years
Sep 21, 2025
-
3 000 Seconds To Minutes
Sep 21, 2025
-
Calorie Calculator For Bicycle Riding
Sep 21, 2025
-
How Many Miles Is 15km
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 10 Out Of 12 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.