11 Out Of 15 Percent
wordexpert
Sep 11, 2025 · 6 min read
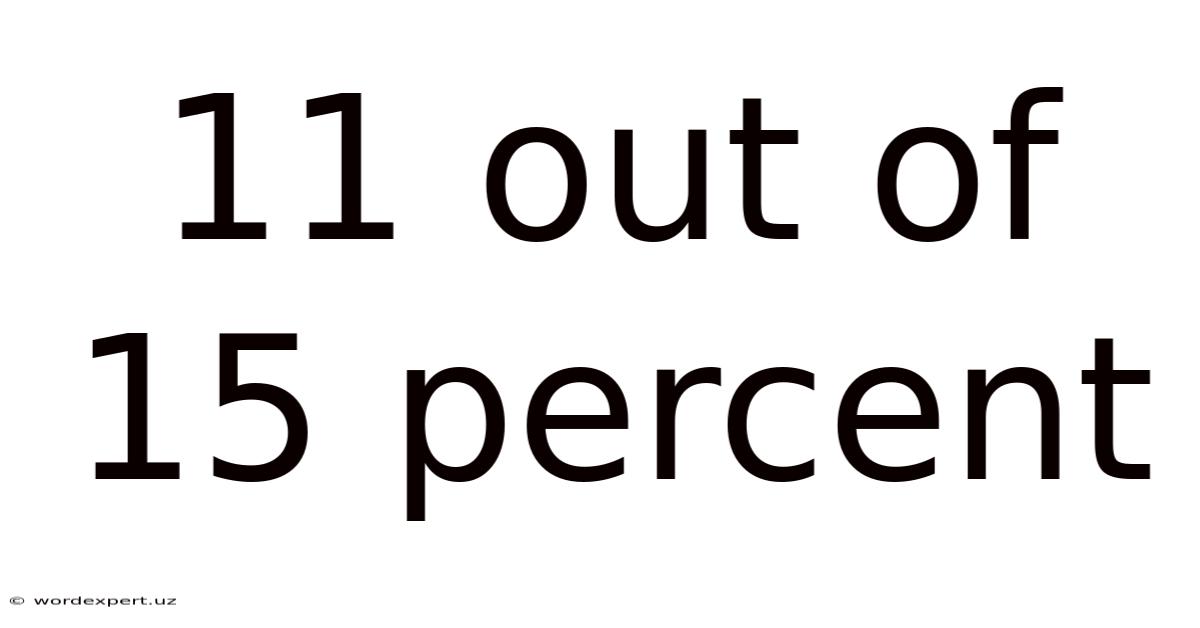
Table of Contents
Understanding 11 out of 15: Fractions, Percentages, and Real-World Applications
Understanding fractions and percentages is a fundamental skill applicable across numerous aspects of life, from calculating discounts in a store to analyzing data in a scientific report. This article delves into the meaning of "11 out of 15," exploring its representation as a fraction, a percentage, and its implications in various contexts. We'll also examine how to perform calculations involving such figures, providing clear examples to solidify your understanding.
1. Expressing "11 out of 15" as a Fraction
The statement "11 out of 15" directly translates into a fraction: 11/15. The numerator (11) represents the part, while the denominator (15) represents the whole. This fraction is already in its simplest form, as 11 and 15 share no common factors other than 1. This means we cannot simplify it further by dividing both the numerator and the denominator by the same number.
2. Converting the Fraction to a Percentage
To express 11/15 as a percentage, we need to convert the fraction into an equivalent fraction with a denominator of 100. We can achieve this by dividing 11 by 15 and then multiplying the result by 100:
11 ÷ 15 ≈ 0.7333
0.7333 × 100 ≈ 73.33%
Therefore, 11 out of 15 is approximately 73.33%. The use of "approximately" is crucial because the decimal representation of 11/15 is a recurring decimal (0.7333...). For practical purposes, rounding to two decimal places (73.33%) is usually sufficient.
3. Real-World Applications: Understanding the Context
The interpretation of "11 out of 15" heavily depends on the context. Consider these examples:
-
Academic Performance: If a student answered 11 out of 15 questions correctly on a test, their score would be 73.33%. This would be considered a good score, but the actual significance depends on the grading scale used by the instructor. A seemingly small difference in the number of correct answers can dramatically alter the percentage and overall grade. For instance, 12 out of 15 is 80%, showcasing the impact of each correct answer.
-
Survey Results: If 11 out of 15 respondents in a survey agreed with a particular statement, it suggests a strong level of agreement (73.33%). However, the sample size (15) is relatively small, potentially limiting the generalizability of the results to a larger population. Larger sample sizes yield more reliable and statistically significant results.
-
Manufacturing Quality Control: In a manufacturing process where 15 items are inspected, and 11 meet quality standards, the yield is 73.33%. This indicates a reasonably high success rate, but further investigation might be needed to identify the reasons for the remaining 4 (26.67%) items failing to meet standards. Continuous improvement efforts would aim to increase this percentage.
-
Sports Statistics: If a basketball player made 11 out of 15 free throws, their free-throw percentage is 73.33%. This statistic reflects the player's accuracy in free throws and is a key performance indicator (KPI) for basketball players. Small variations in this percentage can impact a player's overall performance and team success.
4. Calculations Involving 11/15 and 73.33%
Let's explore some practical calculations using 11/15 and its percentage equivalent:
- Finding a Part of a Whole: If there are 30 items in total, and 73.33% meet the standard, how many items meet the standard? We can calculate this by multiplying the total number of items by the percentage (as a decimal):
30 x 0.7333 ≈ 22
Approximately 22 items meet the standard.
- Finding the Total from a Part: If 22 items meet the standard, and this represents 73.33% of the total, how many items are there in total? We can set up a proportion:
22 / Total = 0.7333 / 1
Solving for the total:
Total = 22 / 0.7333 ≈ 30
There are approximately 30 items in total.
- Comparing Percentages: Suppose another process has a success rate of 80%. Comparing this to our 73.33% success rate shows a clear difference of 6.67% (80% - 73.33%). This difference can be significant depending on the context and the implications of the performance discrepancy.
5. Understanding the Limitations of Percentages
While percentages are useful for quick comparisons and understanding proportions, they can be misleading if not interpreted carefully. Always consider the following:
-
Sample Size: As mentioned earlier, small sample sizes can lead to unreliable results. A 73.33% success rate based on a sample of 15 might not be representative of the larger population.
-
Context: The significance of a percentage depends entirely on the context. A 73.33% success rate in one situation might be excellent, while in another it could be considered poor.
-
Rounding Errors: Rounding percentages can introduce small errors, especially when performing multiple calculations. It's important to maintain sufficient precision throughout your calculations to minimize these errors.
6. Advanced Concepts: Standard Deviation and Confidence Intervals
For more rigorous analysis, especially when dealing with larger datasets, incorporating statistical concepts like standard deviation and confidence intervals is crucial. These measures provide a better understanding of the variability and reliability of the percentage. Standard deviation quantifies the dispersion of data around the mean (average), while a confidence interval provides a range of values within which the true population percentage likely lies with a specified level of confidence (e.g., 95%).
7. Frequently Asked Questions (FAQ)
-
Q: Can 11/15 be expressed as a decimal?
- A: Yes, 11/15 is approximately equal to 0.7333 (a recurring decimal).
-
Q: Is 73.33% a good percentage?
- A: The goodness of 73.33% entirely depends on the context. In some scenarios, it might be excellent, while in others, it could be considered poor.
-
Q: How do I calculate the percentage increase or decrease from 11/15 to another percentage?
- A: To calculate the percentage change, find the difference between the two percentages and divide by the original percentage. Then, multiply the result by 100 to express it as a percentage.
-
Q: What are some alternative ways to represent "11 out of 15"?
- A: You could say "11 in 15," or express it as a ratio (11:15).
8. Conclusion
Understanding "11 out of 15" involves more than just recognizing its fractional and percentage representations. It necessitates comprehending the context, performing relevant calculations, and appreciating the limitations of percentages. By grasping these concepts, you equip yourself with valuable analytical skills applicable to various domains, from academic assessments to business analysis and beyond. Remember to always consider the context, sample size, and potential for error when interpreting percentages. The ability to confidently navigate fractions and percentages is a cornerstone of numerical literacy and empowers you to make informed decisions based on data analysis.
Latest Posts
Latest Posts
-
How Many Grams In Quart
Sep 11, 2025
-
How To Sedate A Cat
Sep 11, 2025
-
Minus 10 Celsius To Fahrenheit
Sep 11, 2025
-
How Far Is 30 Kilometers
Sep 11, 2025
-
How Long Is 71 Weeks
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 11 Out Of 15 Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.