15 3/4 Divided By 2
wordexpert
Sep 21, 2025 · 6 min read
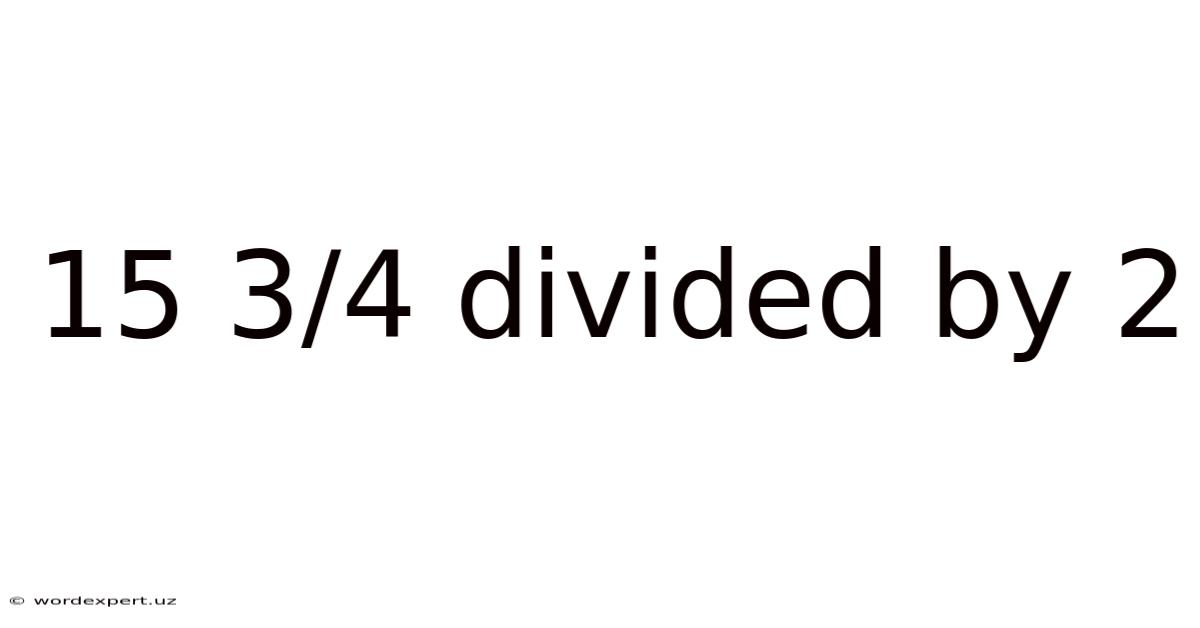
Table of Contents
15 3/4 Divided by 2: A Deep Dive into Fraction Division
Dividing mixed numbers can seem daunting, but with a clear understanding of the underlying principles, it becomes a straightforward process. This article will guide you through the steps of dividing 15 3/4 by 2, explaining the process in detail and exploring the mathematical concepts involved. We'll delve into various methods, ensuring you not only understand how to solve this specific problem but also gain the skills to tackle similar calculations with confidence. This comprehensive guide will equip you with the knowledge to confidently approach fraction division in any context.
Understanding Mixed Numbers and Fractions
Before we tackle the division, let's refresh our understanding of mixed numbers and fractions. A mixed number combines a whole number and a fraction, like 15 3/4. This represents 15 whole units and an additional 3/4 of a unit. A fraction, on the other hand, expresses a part of a whole, with the numerator (top number) representing the parts we have and the denominator (bottom number) representing the total number of parts the whole is divided into.
In the mixed number 15 3/4, 15 is the whole number part, and 3/4 is the fractional part. To perform division, it's often simpler to convert this mixed number into an improper fraction.
Converting Mixed Numbers to Improper Fractions
An improper fraction has a numerator larger than or equal to its denominator. To convert 15 3/4 into an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: 15 * 4 = 60
- Add the numerator: 60 + 3 = 63
- Keep the same denominator: The denominator remains 4.
Therefore, 15 3/4 is equal to the improper fraction 63/4. This conversion is crucial for simplifying the division process.
Method 1: Dividing Improper Fractions
Now that we've converted 15 3/4 to 63/4, we can proceed with the division: 63/4 ÷ 2. Dividing by a whole number is equivalent to multiplying by its reciprocal. The reciprocal of 2 is 1/2. So our calculation becomes:
63/4 * 1/2 = (63 * 1) / (4 * 2) = 63/8
This improper fraction, 63/8, represents our answer. However, it's usually more convenient to express the answer as a mixed number.
Converting Improper Fractions to Mixed Numbers
To convert 63/8 back to a mixed number, we perform the following steps:
- Divide the numerator by the denominator: 63 ÷ 8 = 7 with a remainder of 7.
- The quotient becomes the whole number part: The quotient, 7, is the whole number part of our mixed number.
- The remainder becomes the numerator of the fractional part: The remainder, 7, becomes the numerator.
- The denominator remains the same: The denominator remains 8.
Therefore, 63/8 is equal to 7 7/8. This is our final answer: 15 3/4 divided by 2 equals 7 7/8.
Method 2: Dividing Each Part Separately
Alternatively, we can divide the whole number and fractional parts separately. This approach might seem less efficient, but it can be helpful for visualizing the process:
- Divide the whole number: 15 ÷ 2 = 7 with a remainder of 1. This means we have 7 whole units.
- Convert the remainder to a fraction: The remainder of 1 represents 1 whole unit, which is equal to 4/4 (since our denominator is 4).
- Add the remaining fraction: We add the original fractional part (3/4) to the remainder expressed as a fraction (4/4): 4/4 + 3/4 = 7/4.
- Divide the fractional part: 7/4 ÷ 2 = 7/4 * 1/2 = 7/8
- Combine the results: The whole number part is 7 and the fractional part is 7/8. Therefore, the final answer is 7 7/8.
Method 3: Decimal Conversion
Another approach involves converting the mixed number into a decimal before dividing. This method is particularly useful if you're comfortable working with decimals.
- Convert the mixed number to a decimal: 15 3/4 = 15.75
- Divide the decimal: 15.75 ÷ 2 = 7.875
- Convert the decimal back to a fraction (optional): 0.875 = 7/8 This converts back to the same mixed number: 7 7/8
The Mathematical Rationale Behind Fraction Division
The core principle behind dividing fractions is understanding the concept of reciprocals. Dividing by a number is the same as multiplying by its reciprocal. The reciprocal of a fraction is obtained by switching the numerator and the denominator. For instance, the reciprocal of 2/3 is 3/2.
When dividing a fraction by a whole number (as in our case), we treat the whole number as a fraction with a denominator of 1. For example, 2 is equivalent to 2/1. Therefore, dividing 63/4 by 2 is the same as multiplying 63/4 by 1/2.
Practical Applications and Real-World Examples
Understanding fraction division is crucial for a wide range of applications. Consider these examples:
- Baking: If a recipe calls for 15 3/4 cups of flour and you want to halve the recipe, you'd need to divide 15 3/4 by 2.
- Sewing: Calculating fabric requirements often involves dividing lengths and widths, which might involve fractions.
- Construction: Precise measurements in construction projects frequently require working with fractions and mixed numbers.
- Engineering: Many engineering calculations involve fraction division for accurate measurements and proportions.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve this problem?
A: Yes, most calculators can handle fraction division. However, understanding the manual process is vital for grasping the underlying mathematical concepts.
Q: What if the divisor was a fraction instead of a whole number?
A: The principle remains the same: convert all mixed numbers to improper fractions and then multiply by the reciprocal of the divisor.
Q: Why is it important to convert mixed numbers to improper fractions before dividing?
A: Converting to improper fractions simplifies the calculation, making it easier to apply the rules of fraction multiplication and avoiding potential errors in handling the whole number and fractional parts separately.
Q: Are there other methods to solve this problem?
A: While the methods explained are the most common and straightforward, there are other advanced techniques involving long division with fractions that can be explored for a deeper understanding.
Conclusion
Dividing 15 3/4 by 2, although initially appearing complex, becomes manageable with a systematic approach. By converting the mixed number to an improper fraction and then applying the principles of fraction division, we arrive at the correct answer: 7 7/8. Understanding the different methods and their underlying rationale not only helps solve this specific problem but also equips you with the necessary skills to tackle a broad range of fraction division problems confidently and efficiently. Remember to practice regularly to reinforce your understanding and build proficiency in this essential mathematical skill. The ability to confidently manipulate fractions and mixed numbers is a cornerstone of mathematical literacy and has practical applications across numerous fields.
Latest Posts
Latest Posts
-
45 Out Of 50 Percentage
Sep 22, 2025
-
How Long Till 2 20
Sep 22, 2025
-
6 8 Ounces Of Water
Sep 22, 2025
-
200 Ml To Fl Oz
Sep 22, 2025
-
Uk Pint Vs Us Pint
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 15 3/4 Divided By 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.