19 25 As A Percent
wordexpert
Sep 17, 2025 · 5 min read
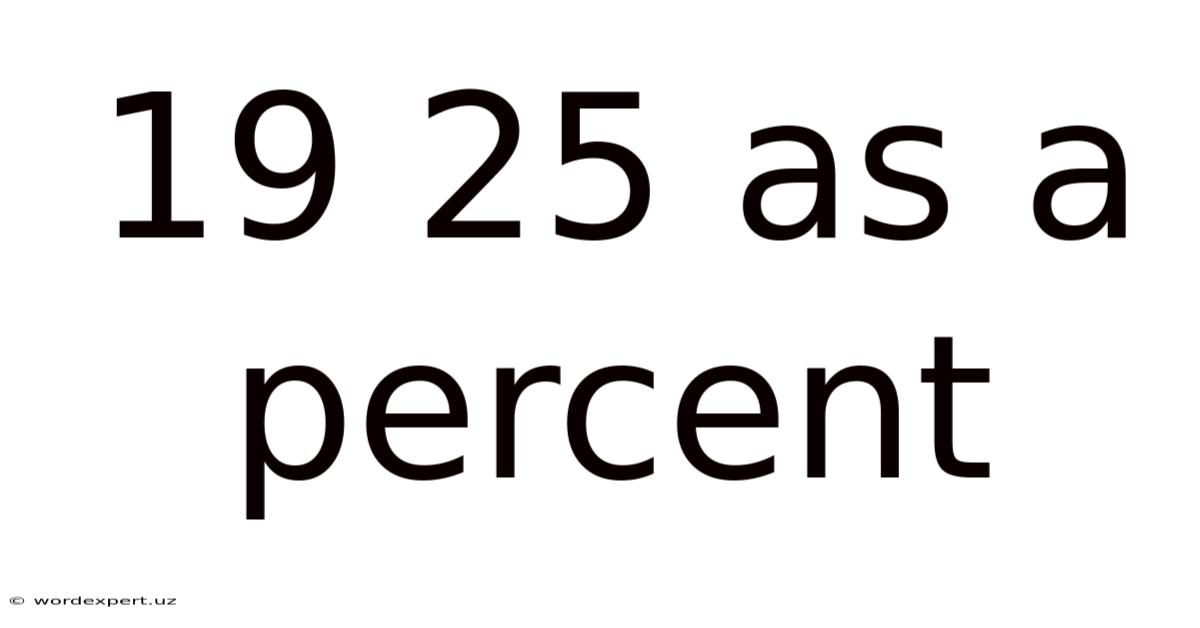
Table of Contents
19/25 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Converting fractions to percentages is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced statistical analysis. This comprehensive guide will delve into the process of converting the fraction 19/25 to a percentage, explaining the underlying principles and providing practical examples. We'll explore different methods, address common misconceptions, and even touch upon the broader context of fraction-to-percentage conversions. Understanding this simple yet powerful conversion is key to navigating the numerical world efficiently and accurately.
Understanding Percentages and Fractions
Before we dive into the conversion, let's solidify our understanding of percentages and fractions. A percentage represents a fraction of 100. The symbol "%" denotes "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
A fraction, on the other hand, expresses a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of equal parts. For instance, in the fraction 19/25, 19 represents the number of parts, and 25 represents the total number of equal parts.
Method 1: The Direct Conversion Method
The most straightforward method to convert 19/25 to a percentage is by using the fundamental principle of percentages: expressing the fraction as a proportion of 100.
To do this, we need to find an equivalent fraction with a denominator of 100. We can achieve this by multiplying both the numerator and denominator by a number that transforms the denominator into 100. In this case, we multiply both the numerator and denominator of 19/25 by 4:
(19 x 4) / (25 x 4) = 76/100
Since a percentage is a fraction out of 100, 76/100 directly translates to 76%. Therefore, 19/25 is equal to 76%.
Method 2: The Decimal Conversion Method
An alternative method involves converting the fraction to a decimal first, then multiplying by 100 to obtain the percentage.
-
Convert the fraction to a decimal: Divide the numerator (19) by the denominator (25): 19 ÷ 25 = 0.76
-
Multiply the decimal by 100: 0.76 x 100 = 76
-
Add the percentage symbol: 76%
This method confirms that 19/25 is indeed equal to 76%.
Method 3: Using Proportions
We can also approach this using proportions. We can set up a proportion where x represents the percentage we are trying to find:
19/25 = x/100
To solve for x, we cross-multiply:
19 * 100 = 25 * x
1900 = 25x
x = 1900 / 25
x = 76
Therefore, x = 76%, confirming our previous results.
Real-World Applications of Fraction-to-Percentage Conversions
The ability to convert fractions to percentages is invaluable in various real-world scenarios. Here are a few examples:
-
Calculating Grades: If a student answers 19 out of 25 questions correctly on a test, their score is 76%.
-
Analyzing Sales Data: If a company sells 19 out of 25 units of a product, their sales percentage for that product is 76%.
-
Determining Financial Performance: If a company's profits represent 19 out of 25 of its revenue, its profit margin is 76%.
-
Understanding Survey Results: If 19 out of 25 respondents agree with a particular statement in a survey, the agreement rate is 76%.
-
Recipe Scaling: If a recipe calls for 19 grams of an ingredient out of a total of 25 grams of ingredients, that ingredient represents 76% of the total weight.
Common Misconceptions
A common misconception is that converting fractions to percentages always involves a direct multiplication by 100. While this is true for fractions with denominators that are factors of 100 (like 25, 50, or 100), it's not always the case. For other denominators, you need to first find an equivalent fraction with a denominator of 100 or convert the fraction to a decimal first.
Advanced Applications: Beyond Simple Fractions
The principles discussed above can be extended to more complex scenarios. For instance, you can apply the same methods to convert fractions with larger numbers or even mixed numbers (numbers containing both a whole number and a fraction). The key is to follow the fundamental steps: either find an equivalent fraction with a denominator of 100 or convert to a decimal first and then multiply by 100.
Frequently Asked Questions (FAQ)
Q: Can I convert any fraction to a percentage?
A: Yes, absolutely. Any fraction can be converted to a percentage by following the methods outlined above.
Q: What if the percentage is a decimal?
A: If the calculation results in a decimal percentage (e.g., 76.5%), you can round it to the nearest whole number (77%) or keep it as a decimal percentage depending on the required level of precision.
Q: Are there any online tools to help with fraction-to-percentage conversions?
A: Yes, many online calculators are readily available to perform this conversion. However, understanding the underlying mathematical principles is crucial for problem-solving beyond simple calculations.
Q: What is the relationship between fractions, decimals, and percentages?
A: They are all different ways of representing the same quantity. A fraction shows a part of a whole using a numerator and a denominator; a decimal uses a base-ten system; and a percentage expresses a fraction as a proportion of 100. They are all interchangeable.
Conclusion
Converting 19/25 to a percentage demonstrates a fundamental mathematical concept with practical applications across numerous fields. The three methods presented – the direct conversion, decimal conversion, and proportion methods – provide flexible approaches to solve this type of problem. Understanding these methods and the underlying relationship between fractions and percentages empowers you to confidently tackle numerical challenges in various contexts, making you a more proficient problem-solver. By grasping these concepts, you enhance your mathematical skills and improve your ability to analyze and interpret data effectively. Remember that the core principle remains consistent: representing a part of a whole as a fraction of 100.
Latest Posts
Latest Posts
-
Inches Of Water To Psig
Sep 17, 2025
-
How To Measure Chest Size
Sep 17, 2025
-
90 Days From March 12th
Sep 17, 2025
-
6 To The 5th Power
Sep 17, 2025
-
Find Slant Height Of Pyramid
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 19 25 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.