2 3 Plus 2 3
wordexpert
Sep 25, 2025 · 4 min read
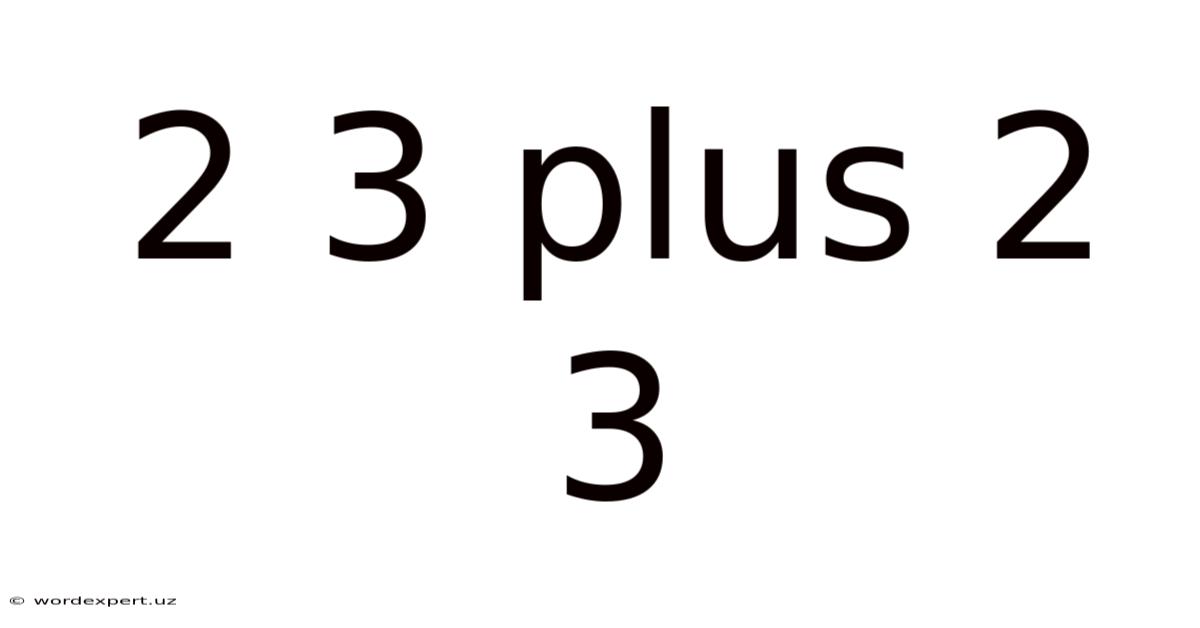
Table of Contents
Decoding 2³ + 2³: A Deep Dive into Exponential Expressions and Their Applications
This article explores the seemingly simple mathematical expression 2³ + 2³, delving far beyond the immediate answer to uncover the underlying principles, practical applications, and broader mathematical concepts it represents. We'll break down the calculation step-by-step, examine the properties of exponents, and explore how this type of problem appears in various fields, from computer science to physics. Understanding this seemingly simple equation unlocks a world of mathematical understanding.
Understanding the Basics: Exponents and Cubes
Before we tackle 2³ + 2³, let's solidify our understanding of the core components: exponents and cubes. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. In the expression 2³, the '2' is the base and the '3' is the exponent. This means 2³ is equivalent to 2 x 2 x 2. A cube specifically refers to a number raised to the power of 3. Therefore, 2³ is "2 cubed."
Calculating 2³ + 2³: A Step-by-Step Approach
Now, let's solve the expression:
-
Calculate each cube: First, we calculate 2³ individually. 2³ = 2 x 2 x 2 = 8.
-
Add the results: Next, we add the two results together: 8 + 8 = 16.
Therefore, 2³ + 2³ = 16. This seemingly simple calculation forms the bedrock for understanding more complex mathematical concepts.
Beyond the Calculation: Exploring Mathematical Properties
While the calculation itself is straightforward, exploring the mathematical properties involved reveals deeper insights. This expression showcases several fundamental concepts:
-
Associative Property of Addition: The order in which we add the numbers doesn't change the result. We could have written (2³) + (2³) or (2 + 2)³ (incorrect!), but the outcome remains the same for addition. This is crucial for understanding more complex equations.
-
Commutative Property of Addition: We can switch the order of the numbers being added without affecting the sum. 8 + 8 is the same as 8 + 8. While seemingly obvious here, this property is essential for more intricate algebraic manipulations.
-
Distributive Property (for similar expressions): While not directly applicable to this specific problem in its simplest form, consider a similar expression like 2³ + 3(2³). Here, the distributive property allows us to factor out 2³: 2³ (1 + 3) = 2³(4) = 8(4) = 32. This highlights how understanding these properties enables simplification of more complex expressions.
Extending the Concept: Generalizing the Expression
Let's generalize the expression to x³ + x³. This allows us to explore the concept for any value of x. The solution becomes 2x³. This generalization allows us to apply the same principle to various mathematical contexts and problem-solving scenarios. For example, if x = 5, then 5³ + 5³ = 2(5³) = 2(125) = 250.
Real-World Applications: Where This Equation Appears
While seemingly basic, the concepts demonstrated by 2³ + 2³ and its generalization have far-reaching applications in diverse fields:
-
Computer Science: Binary systems, the foundation of computer logic, use powers of 2 extensively. Understanding exponents is critical for calculating memory sizes, processing speeds, and data storage capacities. Expressions involving powers of 2 frequently appear in algorithms and data structures.
-
Physics: Many physical phenomena, such as radioactive decay or the behavior of certain waves, are modeled using exponential functions. Understanding the principles of exponents is crucial for analyzing and predicting these events. Think of calculating the volume of a cube-shaped object.
-
Engineering: Engineers use exponents to model various aspects of design and construction, from structural stability to fluid dynamics. Calculating the volume or surface area of cubic structures, for instance, relies on understanding exponential expressions.
-
Finance: Compound interest calculations heavily rely on exponential growth. Understanding how exponents work is essential for financial planning and investment analysis.
Frequently Asked Questions (FAQs)
-
What is the difference between 2³ and 2 x 3? 2³ (2 cubed) means 2 multiplied by itself three times (2 x 2 x 2 = 8), while 2 x 3 simply means 2 multiplied by 3 (2 x 3 = 6). They are distinct operations leading to different results.
-
Can I simplify 2³ + 2³ further? Yes, as we've shown, 2³ + 2³ simplifies to 2(2³) = 16 or 2x³ in the generalized form. This type of simplification demonstrates efficiency in mathematical problem-solving.
-
What if the base number was different? The principles remain the same. For example, 3³ + 3³ = 2(3³) = 2(27) = 54, or x³ + x³ = 2x³ for any value of x.
-
What are some other examples of exponential expressions? Many exist, including 5², 10⁴, (1/2)³, and even more complex expressions with variables and multiple exponents.
Conclusion: The Significance of a Simple Equation
While 2³ + 2³ = 16 might seem like a trivial equation, it serves as a gateway to understanding a vast range of mathematical concepts and their real-world applications. By dissecting this seemingly simple expression, we've explored exponents, cubic numbers, and various mathematical properties that are fundamental to numerous fields. The ability to generalize the expression allows us to adapt this knowledge to a broad spectrum of problems, solidifying its importance in various mathematical and scientific contexts. Mastering the basics, like this simple equation, is crucial for building a strong foundation in mathematics and appreciating its pervasive influence in our world.
Latest Posts
Latest Posts
-
24 30 As A Percent
Sep 25, 2025
-
How Many Days Till Valentine
Sep 25, 2025
-
What Is 40 Of 70
Sep 25, 2025
-
90 000 Pennies To Dollars
Sep 25, 2025
-
Cuantos Onzas Tiene Un Gramo
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 2 3 Plus 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.