2 5 Divided By 6
wordexpert
Sep 11, 2025 · 6 min read
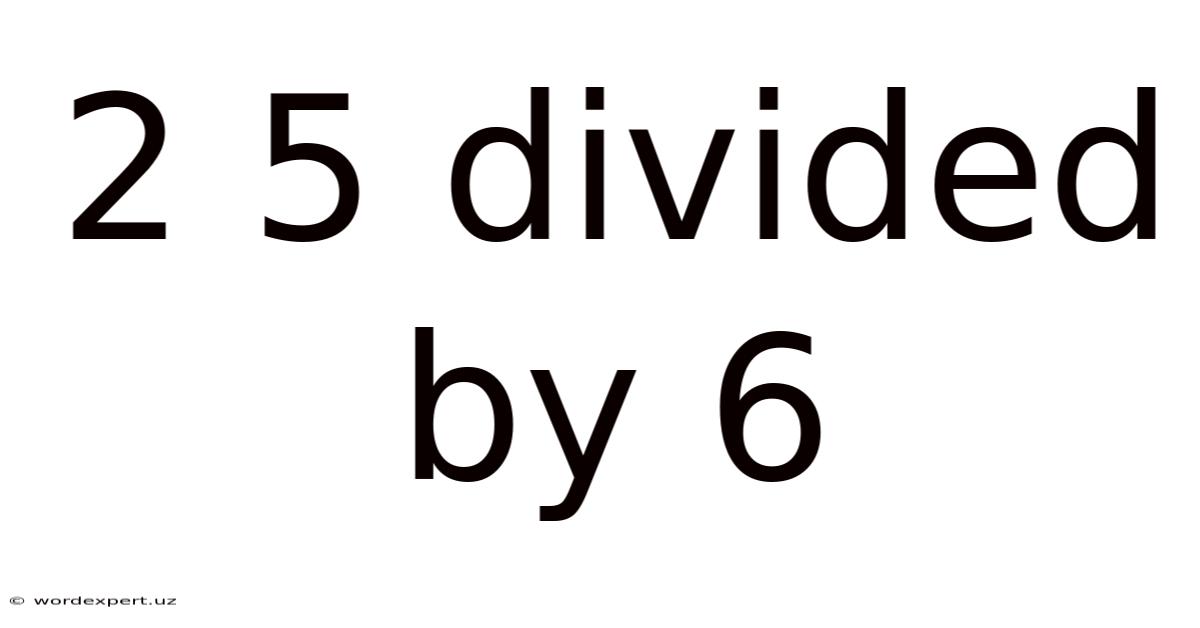
Table of Contents
Decoding 25 Divided by 6: A Comprehensive Exploration of Division and Remainders
This article delves into the seemingly simple mathematical problem of 25 divided by 6, exploring not just the answer but the underlying principles of division, remainders, and their practical applications. Understanding this seemingly basic calculation unlocks a deeper comprehension of fundamental mathematical concepts crucial for various fields, from everyday budgeting to advanced engineering. We'll cover the process step-by-step, explain the concept of remainders, and explore various ways to represent the solution, making this concept accessible to everyone, regardless of their mathematical background.
Understanding Division: The Basics
Division, at its core, is the process of splitting a quantity into equal parts. Think of it as the opposite of multiplication. If multiplication combines groups of equal size, division separates a larger group into smaller, equal groups. In the equation 25 ÷ 6 (25 divided by 6), we're asking: "How many times does 6 fit into 25?"
Solving 25 Divided by 6: A Step-by-Step Approach
Let's tackle the problem directly. We want to find out how many times 6 goes into 25.
-
Initial Estimation: We can start by estimating. We know that 6 x 4 = 24, and 6 x 5 = 30. Since 25 falls between 24 and 30, we know our answer will be between 4 and 5.
-
Long Division: The most common method for solving this is long division.
4 ____ 6|25 24 -- 1We begin by asking how many times 6 goes into 2 (the first digit of 25). It doesn't go at all, so we move to the next digit, making it 25. Six goes into 25 four times (6 x 4 = 24). We subtract 24 from 25, leaving a remainder of 1.
-
Interpreting the Result: The long division shows us that 6 goes into 25 four times with a remainder of 1. This can be expressed in several ways:
-
Quotient and Remainder: The quotient is 4 (the whole number of times 6 goes into 25), and the remainder is 1 (the amount left over).
-
Mixed Number: We can express the result as a mixed number: 4 1/6. This represents four whole groups of 6, plus one-sixth of another group.
-
Decimal: We can also express the result as a decimal. To do this, we continue the division process by adding a decimal point and a zero to the remainder:
4.166... ____ 6|25.000 24 -- 10 6 -- 40 36 -- 40 36 -- 4...This shows that 25 divided by 6 is approximately 4.1666..., a recurring decimal. The "…" indicates that the digit 6 repeats infinitely.
-
The Significance of the Remainder
The remainder (1 in this case) is a crucial part of the answer. It represents the portion of the dividend (25) that wasn't evenly divisible by the divisor (6). It signifies that we couldn't perfectly split 25 into groups of 6. This remainder is often just as important as the quotient in practical applications.
For example, if you have 25 apples and want to divide them equally among 6 friends, each friend would get 4 apples, and you'd have 1 apple left over. The remainder highlights this leftover quantity.
Practical Applications of Division and Remainders
The concept of division with remainders has widespread applications:
- Sharing and Distribution: Dividing resources (like apples, candy, or money) among a group of people.
- Measurement and Conversions: Converting units of measurement (e.g., converting inches to feet).
- Programming and Computing: Remainders are frequently used in computer algorithms and programming for tasks like indexing and data manipulation.
- Engineering and Design: Calculating dimensions and quantities in engineering projects.
- Everyday Life: Calculating costs per unit, splitting bills, or determining the number of items needed for a project.
Exploring Different Representations: Fractions and Decimals
We've seen how to represent the result as a quotient and remainder, a mixed number, and a decimal. Let's delve deeper into the relationship between these representations.
-
Fraction Representation: The mixed number 4 1/6 directly translates to the improper fraction 25/6. This means 25 parts out of a total of 6 parts. The improper fraction represents the entire quantity as a fraction of the divisor.
-
Decimal Representation: The decimal representation (4.1666...) is an approximation of the exact value. The repeating decimal indicates that the division doesn't terminate; it continues infinitely. The accuracy of the decimal depends on the number of decimal places used. Rounding to two decimal places would give us 4.17. This is an approximation, not the exact value.
Addressing Common Misconceptions
A common mistake is neglecting the remainder or misinterpreting its significance. Remember, the remainder is a vital component of the complete solution, not an insignificant leftover.
Another misconception is assuming that a decimal representation is always superior to a fraction or quotient-remainder representation. Each representation has its merits and is appropriate for different contexts. Sometimes, a precise fraction or the quotient and remainder provide a more meaningful answer than an approximate decimal value.
Frequently Asked Questions (FAQ)
Q: What is the most accurate way to represent 25 divided by 6?
A: The most accurate representation is as a mixed number (4 1/6) or an improper fraction (25/6). Decimal representation (4.1666...) is an approximation because of the repeating decimal.
Q: Why do we get a remainder in division?
A: We get a remainder when the dividend (the number being divided) is not a multiple of the divisor (the number we are dividing by). It signifies that the divisor doesn't divide the dividend evenly.
Q: How do I choose the best way to represent the answer (fraction, decimal, or quotient and remainder)?
A: The best way depends on the context. For sharing items, the quotient and remainder are often most useful. In calculations requiring further mathematical operations, fractions or decimals might be more convenient.
Q: Can the remainder ever be larger than the divisor?
A: No. If the remainder is larger than the divisor, it means the division was not performed correctly. The divisor should go into the remainder at least once.
Q: What happens if we divide by zero?
A: Division by zero is undefined in mathematics. It's an operation that doesn't have a meaningful result.
Conclusion: More Than Just an Answer
The seemingly simple problem of 25 divided by 6 offers a gateway to a deeper understanding of fundamental mathematical concepts. By exploring the different ways to represent the solution and understanding the significance of the remainder, we gain a more nuanced appreciation for division and its applications in various fields. Remember, mathematics is not just about finding answers; it's about understanding the underlying principles and how they apply to the world around us. The next time you encounter a division problem, take a moment to reflect on the process, the different ways to express the solution, and the practical implications of the result. This deeper understanding will strengthen your mathematical foundation and equip you with valuable problem-solving skills applicable far beyond the classroom.
Latest Posts
Latest Posts
-
How Many Grams In Quart
Sep 11, 2025
-
How To Sedate A Cat
Sep 11, 2025
-
Minus 10 Celsius To Fahrenheit
Sep 11, 2025
-
How Far Is 30 Kilometers
Sep 11, 2025
-
How Long Is 71 Weeks
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 2 5 Divided By 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.