2 9 As A Percent
wordexpert
Sep 21, 2025 · 5 min read
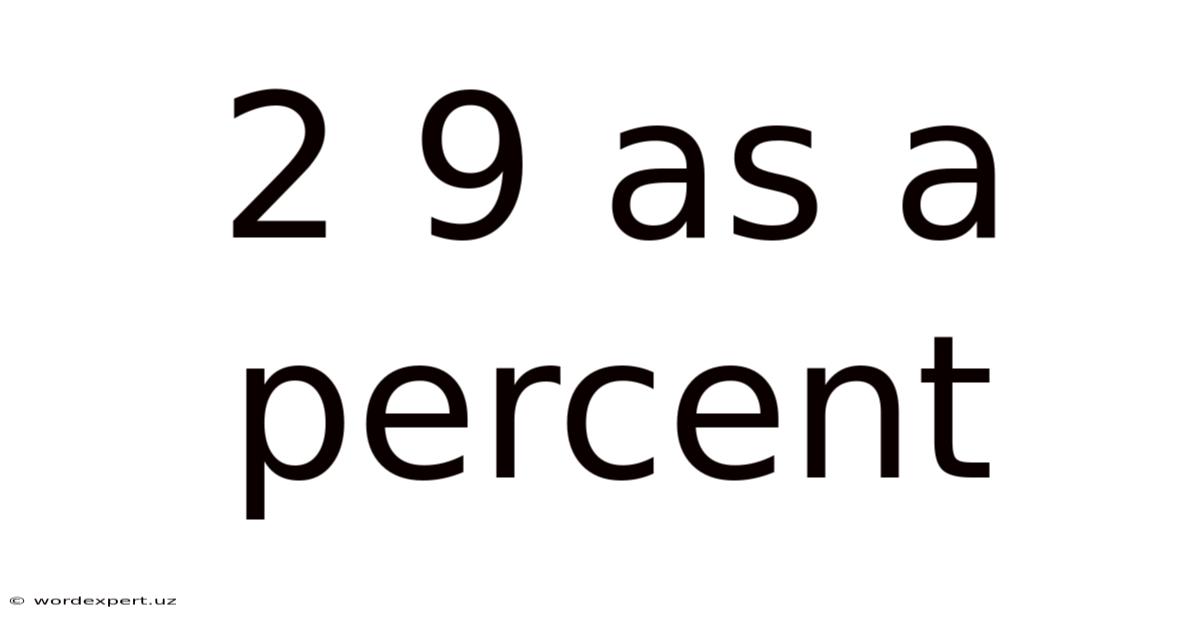
Table of Contents
Decoding 2/9 as a Percentage: A Comprehensive Guide
Understanding fractions and percentages is fundamental to various aspects of life, from calculating discounts in a shop to comprehending financial reports. This article delves into the conversion of the fraction 2/9 into a percentage, providing a step-by-step explanation suitable for all levels of mathematical understanding. We'll explore different methods, address common misconceptions, and equip you with the skills to tackle similar fraction-to-percentage conversions with confidence. This comprehensive guide will cover the basic conversion, explore the underlying mathematical principles, and answer frequently asked questions.
Introduction: The Importance of Percentage Conversions
Percentages provide a standardized way to express proportions and ratios. They're incredibly useful for comparing different quantities and expressing parts of a whole. Converting fractions to percentages is a common mathematical task, applicable in countless real-world situations. Mastering this skill allows for easier interpretation of data and facilitates clearer communication of numerical information. Knowing how to calculate 2/9 as a percentage, and understanding the process involved, is a key building block in improving your numerical literacy.
Method 1: The Direct Conversion Method
The most straightforward approach to converting 2/9 to a percentage involves two simple steps:
-
Convert the fraction to a decimal: Divide the numerator (2) by the denominator (9). This gives us 2 ÷ 9 = 0.2222... (the 2 repeats infinitely).
-
Convert the decimal to a percentage: Multiply the decimal by 100. This means 0.2222... × 100 = 22.222...%.
Therefore, 2/9 is approximately equal to 22.22%. The "..." indicates that the decimal (and therefore the percentage) continues infinitely with the digit 2 repeating. For practical purposes, we usually round the percentage to a suitable number of decimal places, such as 22.22% or 22.2%.
Method 2: Using Equivalent Fractions
An alternative method uses the concept of equivalent fractions. To express a fraction as a percentage, we need to create an equivalent fraction with a denominator of 100. While this isn't directly possible with 2/9, we can find a close approximation.
We can try to find a number that, when multiplied by 9, gets us close to 100. This is a little tricky with 9, but we can use a calculator or long division to find this approximation. Approximating the fraction may introduce slight inaccuracies. We see that 9 multiplied by 11 is 99, which is very close to 100.
- If we multiply the denominator (9) by 11, we get 99. To keep the fraction equivalent, we must also multiply the numerator (2) by 11, resulting in 22/99.
- This fraction is very close to 22/100, which is equivalent to 22%.
This method provides a close approximation to the actual percentage, making it suitable for situations where perfect accuracy isn't paramount. The advantage is that it illustrates the underlying principle of equivalent fractions.
Method 3: Understanding the Underlying Mathematical Principles
The conversion from a fraction to a percentage fundamentally involves expressing the fraction as a proportion of 100. A percentage is simply a fraction with a denominator of 100. The mathematical operation involved is as follows:
(Numerator / Denominator) * 100 = Percentage
In our case: (2 / 9) * 100 ≈ 22.22%
This formula highlights the core concept of expressing a part (the numerator) as a percentage of the whole (the denominator). Understanding this formula empowers you to convert any fraction to a percentage. The calculation, whether done manually or with a calculator, remains consistent.
Addressing Common Misconceptions
One common misconception is assuming that simply multiplying the numerator by 100 gives the percentage. This is incorrect. The numerator represents only part of the whole; the denominator provides the context of the whole. Therefore, dividing by the denominator before multiplying by 100 is crucial.
Another misconception arises when dealing with recurring decimals. Students often struggle with the infinite nature of the repeating decimal 0.222... Understanding that we can round this to a suitable number of decimal places for practical applications is vital.
Practical Applications of 2/9 as a Percentage
The ability to convert 2/9 to a percentage is useful in many real-world situations. For instance:
- Discount calculations: If a store offers a 2/9 discount on an item, you can quickly calculate the discount percentage as approximately 22.22%.
- Data analysis: If 2 out of 9 students passed an exam, the pass rate is approximately 22.22%.
- Financial calculations: Understanding percentage changes in financial statements requires proficiency in fraction-to-percentage conversions.
Further Exploration: Working with More Complex Fractions
The methods described here can be extended to more complex fractions. The key principles remain the same: divide the numerator by the denominator to obtain a decimal, then multiply by 100 to get the percentage. Even fractions with larger numbers or more complex expressions can be approached using the same fundamental principles.
FAQ: Frequently Asked Questions
-
Q: Is 22.22% the exact percentage equivalent of 2/9?
- A: No, it's an approximation. The decimal representation of 2/9 is a recurring decimal (0.222...), meaning the 2s repeat infinitely. 22.22% is a rounded approximation for practical use.
-
Q: Why do we multiply by 100 when converting a decimal to a percentage?
- A: A percentage is always a fraction out of 100. Multiplying by 100 scales the decimal to express it as a proportion of 100.
-
Q: Can I use a calculator for this conversion?
- A: Absolutely! Calculators significantly simplify the process, especially when dealing with more complex fractions.
-
Q: What if the fraction has a large denominator, making the division difficult?
- A: Even with large denominators, the principle remains the same: divide the numerator by the denominator and then multiply by 100. A calculator will greatly assist in these calculations.
-
Q: How do I handle negative fractions?
- A: The process is the same. Convert the fraction to a decimal, multiply by 100, and the resulting percentage will simply have a negative sign.
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages is a fundamental skill with broad applications. We've explored different methods for converting 2/9 to a percentage, focusing on both the practical application and the underlying mathematical principles. By understanding these methods, you can confidently tackle similar conversions and apply this crucial skill in various contexts, from everyday calculations to more complex mathematical problems. Remember that while approximations are often necessary for recurring decimals, the core principles remain consistent, making the conversion process straightforward and accessible to all.
Latest Posts
Latest Posts
-
Difference Between Milligrams And Milliliters
Sep 21, 2025
-
How To Calculate Dart Rate
Sep 21, 2025
-
45 Days From 1 22
Sep 21, 2025
-
40 Days After March 5
Sep 21, 2025
-
220 Sq Meters To Feet
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 2 9 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.