2 Percent Of 50 000
wordexpert
Sep 23, 2025 · 6 min read
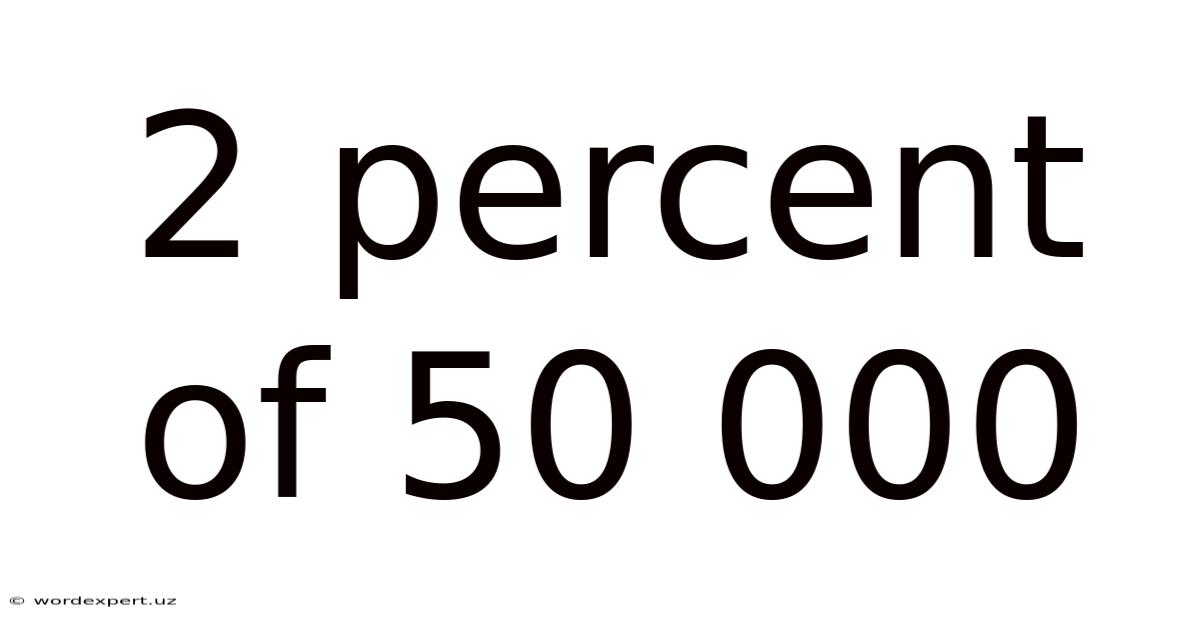
Table of Contents
Decoding 2 Percent of 50,000: A Deep Dive into Percentages and Their Applications
Finding 2 percent of 50,000 might seem like a simple arithmetic problem, easily solved with a calculator. However, understanding the underlying concepts of percentages and their real-world applications extends far beyond this basic calculation. This article will not only show you how to calculate 2% of 50,000 but will also delve into the broader significance of percentages, their uses in various fields, and how to approach similar percentage problems with confidence. This comprehensive guide is designed for anyone, from students needing help with percentages to professionals needing a refresher on practical applications.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." Therefore, 2 percent means 2 out of every 100. This fundamental understanding forms the basis for all percentage calculations. We can represent a percentage as a decimal or a fraction. For example, 2% can be written as 0.02 (decimal) or 2/100 (fraction), which simplifies to 1/50.
This interchangeability is crucial. Understanding how to convert between percentages, decimals, and fractions allows for flexible calculation methods and a deeper comprehension of the underlying mathematical concepts. Let's look at the different ways to calculate 2% of 50,000.
Calculating 2 Percent of 50,000: Three Methods
There are several ways to calculate 2% of 50,000, each offering a slightly different approach and highlighting various aspects of percentage calculations.
Method 1: Using the Decimal Equivalent
This is perhaps the most straightforward method. We convert the percentage (2%) to its decimal equivalent (0.02) and then multiply it by the whole number (50,000).
- Step 1: Convert 2% to a decimal: 2% = 0.02
- Step 2: Multiply the decimal by the whole number: 0.02 x 50,000 = 1000
Therefore, 2% of 50,000 is 1000.
Method 2: Using the Fraction Equivalent
This method uses the fraction equivalent of 2%, which is 2/100 or 1/50. We then multiply this fraction by 50,000.
- Step 1: Convert 2% to a fraction: 2% = 2/100 = 1/50
- Step 2: Multiply the fraction by the whole number: (1/50) x 50,000 = 1000
This method provides a clear visualization of the proportional relationship between the percentage and the whole number.
Method 3: Proportion Method
This method sets up a proportion to solve for the unknown value. We can set it up as follows:
- Step 1: Set up a proportion: 2/100 = x/50,000 (where 'x' represents the unknown value, 2% of 50,000)
- Step 2: Cross-multiply: 100x = 2 * 50,000
- Step 3: Solve for x: 100x = 100,000 => x = 1000
This method is particularly useful for more complex percentage problems where a direct calculation might be less intuitive.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is essential across numerous fields. Let's explore some examples:
-
Finance: Calculating interest on loans, savings accounts, and investments heavily relies on percentage calculations. Understanding compound interest, which involves calculating interest on both the principal and accumulated interest, requires a solid grasp of percentages. For example, if you invest $50,000 and earn a 2% annual return, you'll earn $1000 in the first year.
-
Sales and Marketing: Discounts, sales tax, profit margins, and commission calculations all involve percentages. Retailers frequently offer discounts of a certain percentage, like "20% off," and understanding these calculations is crucial for both businesses and consumers. Analyzing market share, another common task in marketing, often involves working with percentages.
-
Science and Statistics: Data analysis, particularly in fields like epidemiology and demographics, often involves presenting information as percentages. For example, calculating the percentage of a population affected by a disease or the percentage change in a particular variable over time. Statistical significance is frequently determined by comparing percentages or proportions.
-
Everyday Life: Percentages are encountered regularly in everyday scenarios. Calculating tips at restaurants, understanding nutrition labels that express nutrients as percentages of daily recommended values, or determining the percentage increase or decrease in prices are common examples.
Expanding on Percentage Problems: Tackling Variations
Understanding 2% of 50,000 provides a base for tackling more complex percentage problems. Let's consider some variations:
-
Finding the Percentage: Instead of knowing the percentage and finding the part, you might need to find the percentage one value represents of another. For example: "What percentage of 50,000 is 1000?" The solution involves dividing the part (1000) by the whole (50,000) and multiplying by 100: (1000/50,000) * 100 = 2%
-
Finding the Whole: You might know the percentage and the part, but need to find the whole. For instance: "1000 is 2% of what number?" This involves setting up a proportion or using algebraic methods to solve for the unknown. The solution would be 1000/0.02 = 50,000.
-
Percentage Increase/Decrease: Calculating percentage changes is vital in various contexts. For example, if a value increases from 50,000 to 51,000, the percentage increase is calculated as follows: [(51,000 - 50,000)/50,000] * 100 = 2%.
Addressing Common Misconceptions
Several common misconceptions surround percentage calculations. It's important to address these to ensure accuracy and avoid errors:
-
Adding Percentages Directly: It's incorrect to simply add percentages directly when dealing with multiple percentages applied to the same base number. For example, a 10% increase followed by a 10% decrease does not result in the original value; it results in a slight decrease.
-
Confusing Percentage Change with Percentage Points: A change from 10% to 20% is a 10 percentage point increase, but a 100% increase in the percentage itself.
Frequently Asked Questions (FAQs)
Q1: How do I calculate a percentage of a number quickly in my head?
A1: For simpler percentages, mental estimation is helpful. For example, 10% of a number is simply moving the decimal point one place to the left. 5% is half of 10%, and other percentages can be broken down into these simpler components.
Q2: What are the most common mistakes people make when calculating percentages?
A2: Common mistakes include incorrectly converting percentages to decimals, forgetting to multiply by 100 when calculating a percentage from a fraction or ratio, and adding percentages directly without considering the compounding effect.
Q3: Are there any online tools or calculators that can help with percentage calculations?
A3: Many online calculators are available to assist with percentage calculations. These calculators can significantly improve accuracy and efficiency, especially for complex problems.
Conclusion: Mastering Percentages for a Brighter Future
Calculating 2% of 50,000, while seemingly simple, serves as a gateway to a deeper understanding of percentages and their widespread applications. From financial planning to data analysis, a robust grasp of percentages is an invaluable skill for anyone navigating the complexities of the modern world. By understanding the various methods for calculation, addressing common misconceptions, and exploring diverse real-world applications, you can confidently tackle percentage problems and leverage this fundamental mathematical concept to its full potential. Remember, the ability to work with percentages is not just about crunching numbers; it's about developing a critical understanding of proportional relationships and their impact on decision-making across numerous fields.
Latest Posts
Latest Posts
-
60 Days From September 27
Sep 23, 2025
-
60 Months Ago From Today
Sep 23, 2025
-
50 Pints How Many Gallons
Sep 23, 2025
-
Area De Un Circulo Diametro
Sep 23, 2025
-
100 Days From Jan 20
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 2 Percent Of 50 000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.