2 Square Root Of 5
wordexpert
Sep 23, 2025 · 6 min read
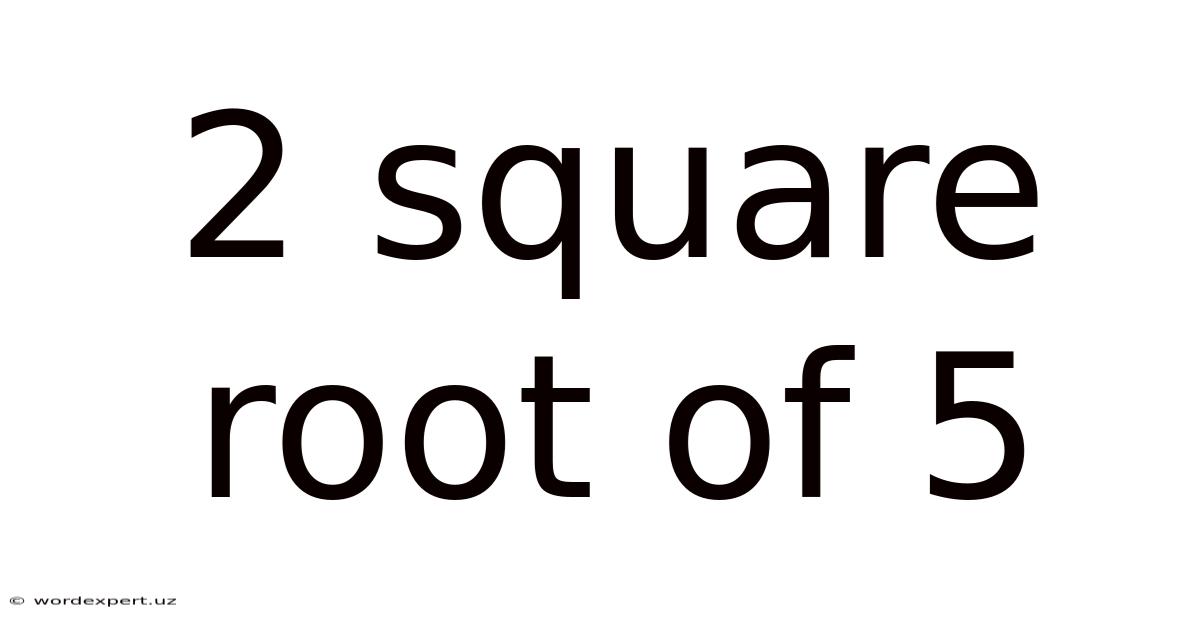
Table of Contents
Unveiling the Mysteries of 2√5: A Deep Dive into Irrational Numbers
The seemingly simple expression "2√5" hides a fascinating world of mathematical concepts. Understanding this number requires exploring the realms of irrational numbers, square roots, and their practical applications. This article will serve as a comprehensive guide, delving into the nature of 2√5, its properties, calculations, and its relevance in various fields. We'll move beyond the basic calculation to uncover the deeper mathematical significance and practical uses of this intriguing number.
Introduction: Understanding Square Roots and Irrational Numbers
Before we delve into the specifics of 2√5, let's establish a firm foundation. The square root of a number (√x) is a value that, when multiplied by itself, equals the original number (x). For example, √9 = 3 because 3 x 3 = 9. However, not all square roots result in whole numbers. Numbers like √2, √3, and √5 are irrational numbers.
Irrational numbers cannot be expressed as a simple fraction (a ratio of two integers). Their decimal representation is non-terminating and non-repeating, meaning it goes on forever without ever settling into a repeating pattern. This is a key characteristic that distinguishes them from rational numbers, which can be expressed as fractions. π (pi) is another famous example of an irrational number.
The number 2√5 combines the concept of a square root with a rational multiplier (2). This means we're essentially dealing with twice the value of the square root of 5. While we can approximate its value, we cannot express it precisely as a fraction or a terminating decimal.
Calculating and Approximating 2√5
While we cannot find an exact decimal representation for 2√5, we can obtain very accurate approximations. The simplest approach involves calculating the square root of 5 first and then multiplying the result by 2.
Most calculators have a square root function. Using a calculator, we find that:
√5 ≈ 2.236067977...
Therefore:
2√5 ≈ 2 * 2.236067977... ≈ 4.472135955...
This approximation is sufficient for many practical purposes. The more decimal places we use, the more precise our approximation becomes. However, it's crucial to remember that this is still an approximation; the true value of 2√5 possesses an infinitely long, non-repeating decimal expansion.
Geometric Interpretation of 2√5
The number 2√5 also has a clear geometric interpretation. Consider a right-angled triangle with two legs of length 2 and 2. Using the Pythagorean theorem (a² + b² = c²), we can calculate the length of the hypotenuse (c):
c² = 2² + 2² = 4 + 4 = 8
c = √8 = √(4 x 2) = 2√2
Now, let's consider a different right-angled triangle. This one has legs of length 1 and 2. Using the Pythagorean theorem again:
c² = 1² + 2² = 1 + 4 = 5
c = √5
If we then construct another right-angled triangle with legs of length 2 and √5 we get:
c² = 2² + (√5)² = 4 + 5 = 9
c = √9 = 3
Therefore, 2√5 can be visually represented as the length of the hypotenuse in specific geometric constructions. These visual representations solidify the understanding of the number's magnitude and its relationship to other geometric elements.
2√5 in Different Number Systems
While 2√5 is irrational in the decimal system, its representation in other number systems might offer different perspectives. For example, in the binary number system, its representation would be an infinitely long, non-repeating sequence of 0s and 1s. Similarly, representations in other bases (like hexadecimal or octal) would also be non-terminating and non-repeating. However, the core characteristic of irrationality remains unchanged regardless of the number system used.
Mathematical Operations with 2√5
Performing mathematical operations involving 2√5 requires understanding how to manipulate square roots. Let's examine some examples:
-
Addition/Subtraction: Adding or subtracting 2√5 to/from another number involving √5 simplifies the calculation. For example, 3√5 + 2√5 = 5√5. However, adding it to a rational number results in an irrational sum (e.g., 2√5 + 7 remains an irrational number).
-
Multiplication: Multiplying 2√5 by another number simply involves multiplying the rational parts and leaving the irrational part unchanged. For example, 3 * 2√5 = 6√5. Multiplying two expressions involving √5 often leads to simplification (e.g., (2√5)(3√5) = 6 * 5 = 30).
-
Division: Dividing 2√5 by another number is similar to multiplication—divide the rational parts. For example, (2√5)/2 = √5. Dividing by another expression involving √5 often requires rationalizing the denominator (a process involving multiplying both the numerator and denominator by the conjugate of the denominator to remove the square root from the denominator).
Applications of 2√5 in Real-World Scenarios
While 2√5 might not be as prevalent as π or e (Euler's number) in everyday calculations, it does appear in various contexts, particularly in:
-
Geometry and Trigonometry: As demonstrated earlier, 2√5 can represent the length of sides or diagonals in specific geometric shapes. This makes it relevant in architectural design, engineering calculations, and computer graphics.
-
Physics and Engineering: Many physical phenomena involve square roots, and 2√5 might appear in solutions to equations describing certain processes or systems. For example, certain calculations related to oscillations or wave propagation might involve this number.
-
Approximation and Estimation: Even though we cannot have a precise decimal value for 2√5, its approximate value is used extensively in estimations and estimations in various fields where high precision isn’t always required.
-
Computer Science and Algorithms: The concept of irrational numbers and their approximations are fundamental to various algorithms and computational processes.
Frequently Asked Questions (FAQ)
Q1: Is 2√5 a rational or irrational number?
A1: 2√5 is an irrational number. While it's multiplied by a rational number (2), the presence of √5 (which is irrational) makes the entire expression irrational.
Q2: How can I calculate 2√5 without a calculator?
A2: Precise calculation without a calculator is impossible due to the irrational nature of √5. However, you can use approximation methods like the Babylonian method (or Heron's method) for finding square roots to get an approximate value of √5 and then multiply by 2.
Q3: What is the significance of 2√5 in mathematics?
A3: While not as prominent as π or e, 2√5 holds significance as an example of an irrational number, highlighting the properties and challenges associated with such numbers. Its appearance in various geometric problems and its role in demonstrating concepts related to square roots are its main mathematical significances.
Q4: Are there other numbers similar to 2√5?
A4: Yes, there are infinitely many other numbers similar to 2√5. Any number of the form a√b, where a is a rational number and b is a non-perfect square integer, will result in an irrational number.
Conclusion: A Deeper Appreciation of 2√5
This exploration of 2√5 has moved beyond a simple numerical calculation. We've examined the underlying mathematical concepts, including irrational numbers, square roots, and geometric interpretations. By understanding these concepts, we appreciate the rich mathematical tapestry that even seemingly simple numbers like 2√5 represent. While we can only approximate its value, the exploration of its nature deepens our understanding of mathematics and its application across various fields. The seemingly simple expression, therefore, reveals a surprising depth and significance, highlighting the beauty and complexity inherent in the world of numbers.
Latest Posts
Latest Posts
-
Punnett Square Calculator For Baby
Sep 23, 2025
-
64 Square Meters To Feet
Sep 23, 2025
-
10 Percent Of 1 Mil
Sep 23, 2025
-
7 Out Of 10 Percentage
Sep 23, 2025
-
2 Complement To Decimal Calculator
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 2 Square Root Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.