24 27 As A Percentage
wordexpert
Sep 24, 2025 · 5 min read
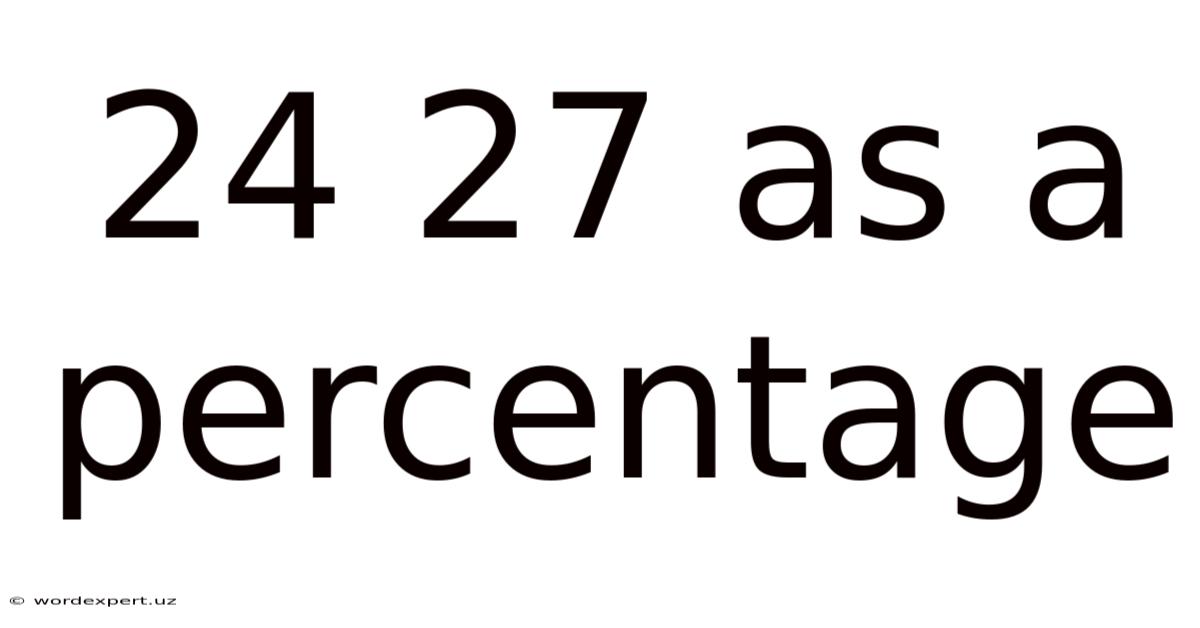
Table of Contents
24 out of 27 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill in math with wide-ranging applications in everyday life, from calculating discounts and taxes to understanding statistics and analyzing data. This article delves into the specific calculation of 24 out of 27 as a percentage, providing a step-by-step explanation, exploring the underlying mathematical principles, and offering practical examples to solidify your understanding. We'll also address common misconceptions and answer frequently asked questions. By the end, you’ll not only know the answer but also grasp the broader concept of percentage calculations.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" (per centum). Therefore, to find a percentage, we determine what proportion of the whole a part represents and then express that proportion as a number out of 100.
Calculating 24 out of 27 as a Percentage: The Step-by-Step Approach
The process of calculating 24 out of 27 as a percentage involves three simple steps:
Step 1: Express the Relationship as a Fraction
First, represent the given information as a fraction. In this case, 24 is the part, and 27 is the whole. This translates to the fraction 24/27.
Step 2: Convert the Fraction to a Decimal
To convert the fraction 24/27 into a decimal, divide the numerator (24) by the denominator (27):
24 ÷ 27 ≈ 0.8889
Note that we've rounded the decimal to four decimal places for accuracy. Depending on the context, you might round to fewer or more decimal places.
Step 3: Convert the Decimal to a Percentage
To convert a decimal to a percentage, multiply the decimal by 100 and add the percent symbol (%):
0.8889 x 100 = 88.89%
Therefore, 24 out of 27 is approximately 88.89%.
Mathematical Principles: Ratios and Proportions
The calculation above relies on the fundamental concepts of ratios and proportions. A ratio compares two quantities, in this instance 24 and 27. A proportion expresses the equality of two ratios. We essentially solved a proportion to find the equivalent fraction with a denominator of 100 (which is the definition of a percentage).
The proportion can be set up as follows:
24/27 = x/100
Solving for x (the percentage):
x = (24/27) * 100 ≈ 88.89
This approach emphasizes the proportional relationship between the part and the whole, providing a deeper mathematical understanding of percentage calculations.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is invaluable in a wide range of real-world situations, including:
-
Financial Calculations: Calculating interest rates, discounts, taxes, profit margins, and investment returns. For example, if a store offers a 20% discount on an item, knowing how to calculate percentages allows you to quickly determine the final price.
-
Academic Assessments: Calculating grades, test scores, and performance metrics. Understanding percentages is crucial for interpreting your academic progress and identifying areas for improvement.
-
Data Analysis: Representing data visually using charts and graphs often involves percentages. Analyzing data expressed as percentages helps in identifying trends, making comparisons, and drawing conclusions.
-
Scientific Research: Many scientific fields use percentages to express probabilities, experimental results, and statistical data.
-
Everyday Life: Determining tips in restaurants, calculating sales tax, and understanding statistics reported in the news all involve percentage calculations.
Common Misconceptions about Percentages
Several common misconceptions surround percentage calculations. It’s essential to address these to avoid errors:
-
Confusing Part and Whole: Accurately identifying the 'part' and the 'whole' is crucial. Incorrectly assigning these values will lead to an incorrect percentage.
-
Incorrect Rounding: The level of rounding should be appropriate to the context. Rounding too aggressively can lead to significant inaccuracies, while excessive decimal places might be unnecessary.
-
Misinterpreting Percentages: Always ensure you understand what the percentage represents. A 10% increase from 100 is different from a 10% decrease from 100.
-
Using percentages without understanding the base: Always consider the context of the percentage. A 10% increase from a small base is different from a 10% increase from a large base.
Advanced Percentage Calculations
While the calculation of 24 out of 27 is relatively straightforward, more complex percentage calculations might involve:
-
Calculating percentage change: Determining the percentage increase or decrease between two values.
-
Calculating percentage points: Understanding the difference between a percentage change and a percentage point change.
-
Working with compound percentages: Calculating percentages when the base changes over time.
Frequently Asked Questions (FAQ)
Q1: How do I calculate a percentage increase or decrease?
To calculate a percentage increase, subtract the original value from the new value, divide the result by the original value, and then multiply by 100. To calculate a percentage decrease, follow the same steps but subtract the new value from the original value.
Q2: What is the difference between a percentage change and percentage points?
A percentage change represents the proportional change between two values. Percentage points represent the arithmetic difference between two percentages. For example, an increase from 10% to 20% is a 100% percentage change but a 10-percentage point increase.
Q3: How can I improve my understanding of percentages?
Practice is key! Work through various percentage problems, starting with simple ones and gradually increasing the complexity. You can find plenty of practice exercises online or in math textbooks. Also, try applying percentages to real-life situations.
Conclusion
Calculating 24 out of 27 as a percentage yields approximately 88.89%. This seemingly simple calculation demonstrates fundamental mathematical principles applicable across numerous fields. By understanding the underlying concepts of ratios, proportions, and the significance of accurate calculations, you can confidently tackle more complex percentage problems and apply this vital skill to everyday situations. Remember to pay close attention to detail, accurately identify the part and whole, and choose an appropriate level of rounding for the specific context. The ability to calculate and interpret percentages is a crucial skill that enhances your understanding of numerical data and contributes to effective problem-solving in diverse contexts.
Latest Posts
Latest Posts
-
Binary To Octal Converter Calculator
Sep 25, 2025
-
How Many Miles Is 1500km
Sep 25, 2025
-
Convert 200 Gm To Oz
Sep 25, 2025
-
15 Out Of 25 Grade
Sep 25, 2025
-
90 Days From 1 16
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 24 27 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.