25 30 As A Percentage
wordexpert
Sep 14, 2025 · 5 min read
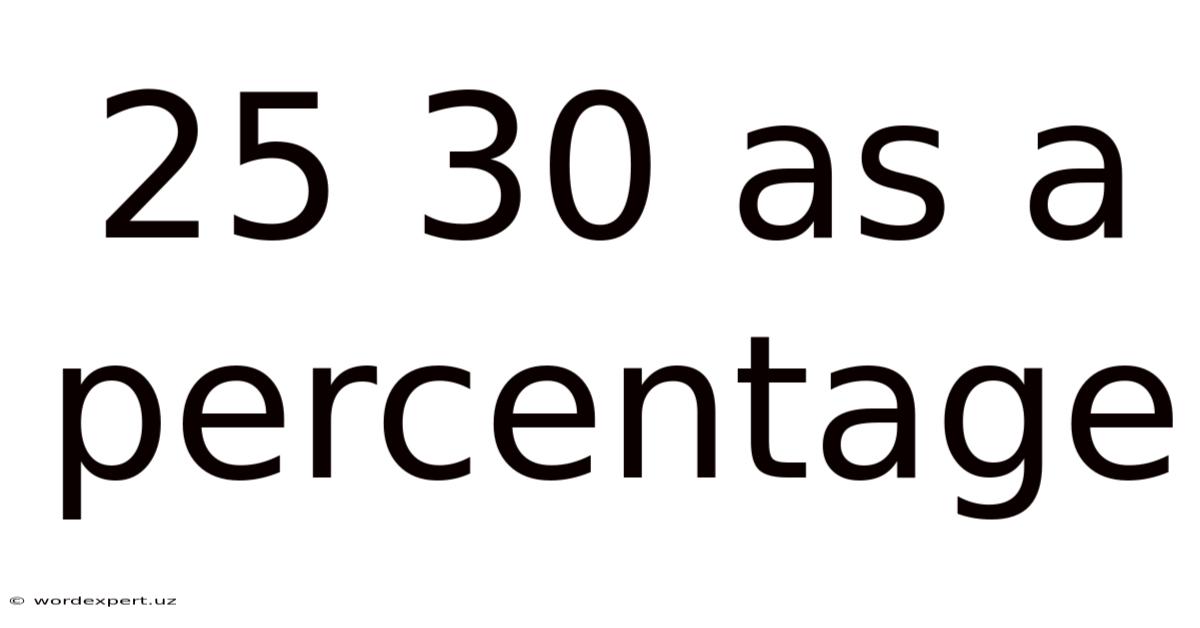
Table of Contents
Decoding 25/30 as a Percentage: A Comprehensive Guide
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in daily life, from calculating discounts and sales tax to comprehending statistics and evaluating performance. This article provides a thorough explanation of how to convert fractions, like 25/30, into percentages, offering multiple approaches and addressing common questions. We'll explore the underlying mathematical concepts and demonstrate practical applications, ensuring a comprehensive understanding for learners of all levels.
Understanding Percentages and Fractions
A percentage represents a fraction out of 100. The symbol "%" signifies "per cent," meaning "out of one hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2. Conversely, any fraction can be expressed as a percentage. To convert a fraction to a percentage, we need to express the fraction as an equivalent fraction with a denominator of 100.
The fraction 25/30 represents 25 parts out of a total of 30 parts. Our goal is to determine what percentage 25 represents when compared to 30.
Method 1: Converting the Fraction to a Decimal, then to a Percentage
This is a common and straightforward method. It involves two steps:
-
Convert the fraction to a decimal: Divide the numerator (25) by the denominator (30).
25 ÷ 30 = 0.8333... (the 3s repeat infinitely)
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the "%" symbol.
0.8333... × 100 = 83.333...%
Therefore, 25/30 is approximately 83.33%. The repeating decimal indicates that the percentage is an approximation. Depending on the context, you might round this to 83.3% or even 83%, depending on the required level of precision.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method directly expresses the fraction as a percentage without involving decimals. However, it's not always feasible, as not all fractions have a simple equivalent with a denominator of 100.
To use this method, we need to find a number that, when multiplied by 30, results in 100. Unfortunately, there's no whole number that satisfies this condition. However, we can simplify the fraction first to make the calculation easier:
-
Simplify the fraction: Both 25 and 30 are divisible by 5.
25 ÷ 5 = 5 30 ÷ 5 = 6
So, 25/30 simplifies to 5/6.
-
Find an equivalent fraction with a denominator of 100 (approximately): We need to find a number that, when multiplied by 6, gives a number close to 100. Multiplying 6 by 16.666... gives 100.
5/6 * (100/6) = 83.333.../100 This is approximately 83.33%.
Method 3: Using a Proportion
This method uses the concept of proportions to solve the problem. A proportion is a statement of equality between two ratios. We can set up a proportion to find the percentage:
25/30 = x/100
To solve for x (the percentage), we cross-multiply:
30x = 2500
x = 2500 ÷ 30
x = 83.333...
Therefore, 25/30 is approximately 83.33%.
Understanding the Significance of Precision
The recurring decimal in our answer (0.8333...) highlights the importance of understanding precision in percentage calculations. In some contexts, rounding to 83% might be sufficient. For instance, if you're calculating a discount, rounding down is typically in the consumer's favor. However, in other contexts, such as scientific calculations or financial reporting, greater precision might be necessary. The level of precision required depends on the specific application.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios:
-
Academic Performance: If a student answers 25 out of 30 questions correctly on a test, their score is 83.33%.
-
Sales and Discounts: A 25% discount on a $30 item reduces the price by $7.50 ($30 * 0.25 = $7.50).
-
Financial Calculations: Interest rates, loan repayments, and investment returns are often expressed as percentages.
-
Data Analysis and Statistics: Percentages are fundamental to interpreting statistical data, such as survey results or market research findings.
-
Recipe Scaling: If a recipe calls for 25 grams of sugar in a 30-gram total mixture, then sugar accounts for approximately 83.33% of the mixture.
These examples demonstrate the ubiquitous nature of percentage calculations in everyday life. Mastering these calculations empowers you to make informed decisions and interpret information more effectively.
Frequently Asked Questions (FAQ)
Q: What if I need to calculate a percentage where the denominator is zero?
A: You cannot divide by zero. A denominator of zero indicates an undefined situation and means a percentage calculation is not possible in that instance.
Q: How do I calculate a percentage increase or decrease?
A: To calculate a percentage increase, find the difference between the new and original values, divide by the original value, and multiply by 100. For a percentage decrease, follow the same steps but subtract the new value from the original value.
Q: Can I use a calculator to convert fractions to percentages?
A: Yes, most calculators have functions to perform these conversions efficiently. Simply divide the numerator by the denominator, and then multiply the result by 100.
Q: Are there any online tools or websites that can help me with percentage calculations?
A: Many websites offer free online percentage calculators that can perform various percentage-related calculations, such as converting fractions to percentages, calculating percentage increases and decreases, and more.
Conclusion
Converting fractions like 25/30 to percentages is a fundamental skill with broad applications. This article explored three different methods, emphasizing the importance of understanding the underlying mathematical principles and the significance of precision in the final answer. By mastering these techniques, you'll be well-equipped to handle percentage calculations confidently in various contexts, enhancing your analytical skills and problem-solving abilities in both academic and real-world situations. Remember, practice makes perfect, so continue working through examples to build your proficiency and understanding of percentages.
Latest Posts
Latest Posts
-
Dew Point Versus Relative Humidity
Sep 14, 2025
-
Convertidor De Oz A Gramos
Sep 14, 2025
-
Whats The Uv Index Tomorrow
Sep 14, 2025
-
3 To The 6th Power
Sep 14, 2025
-
Density Of Water In Lb Ft3
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 25 30 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.