3 4 Divided By 4
wordexpert
Sep 11, 2025 · 5 min read
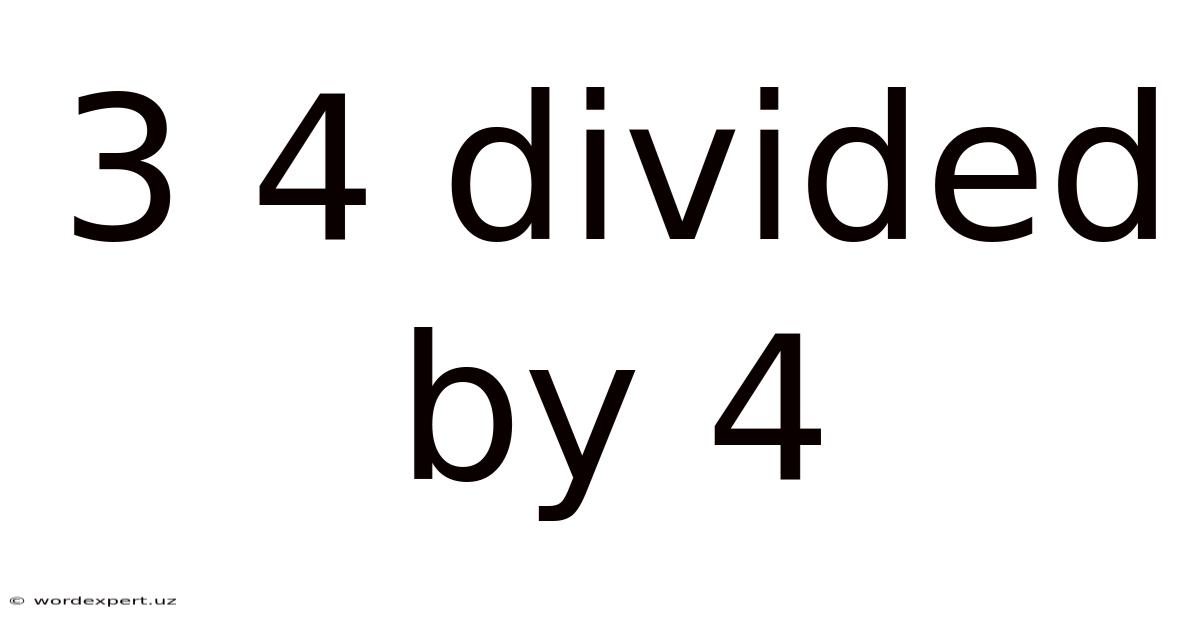
Table of Contents
Decoding 3/4 Divided by 4: A Deep Dive into Fraction Division
Understanding fraction division can seem daunting at first, but with a systematic approach, it becomes surprisingly straightforward. This article will explore the seemingly simple calculation of 3/4 divided by 4, breaking down the process step-by-step, providing multiple methods for solving it, and delving into the underlying mathematical principles. We'll also address common misconceptions and answer frequently asked questions, ensuring a comprehensive understanding for learners of all levels. This exploration goes beyond a simple answer; it's about mastering the concept of dividing fractions.
Understanding the Problem: 3/4 ÷ 4
At its core, the problem "3/4 divided by 4" asks: "How many times does 4 fit into 3/4?" This question highlights the key concept in fraction division: we're determining how many portions of size 4 are contained within a portion of size 3/4. Intuitively, we expect the answer to be a fraction smaller than 1, since 4 is larger than 3/4.
Method 1: The Reciprocal Method
The most common and efficient method for dividing fractions is using the reciprocal. The reciprocal of a number is simply 1 divided by that number. To divide by a fraction, we multiply by its reciprocal.
Step 1: Rewrite the problem as a multiplication problem.
Instead of 3/4 ÷ 4, we rewrite it as 3/4 multiplied by the reciprocal of 4. The reciprocal of 4 (or 4/1) is 1/4. So the problem becomes:
3/4 × 1/4
Step 2: Multiply the numerators and denominators.
To multiply fractions, we multiply the numerators (the top numbers) together and the denominators (the bottom numbers) together.
(3 × 1) / (4 × 4) = 3/16
Therefore, 3/4 divided by 4 is equal to 3/16.
Method 2: Visual Representation
Visualizing the problem can aid understanding. Imagine a pizza cut into four equal slices. 3/4 represents three of these slices. Now, we need to divide these three slices into four equal groups. Each group will consist of 3/16 of the original pizza.
Imagine dividing each of the three slices into four equal parts. You'd then have 12 smaller pieces (3 slices x 4 parts each). If you divide these 12 smaller pieces into 4 equal groups, you will have 3 pieces in each group. Since each piece represents 1/16 of the whole pizza (1/4 divided by 4 = 1/16), each of your four groups contains 3/16 of the pizza. This visual reinforces the answer: 3/16.
Method 3: Converting to Decimal
Another approach involves converting the fraction to its decimal equivalent before performing the division.
Step 1: Convert the fraction to a decimal.
3/4 is equal to 0.75 (because 3 divided by 4 is 0.75).
Step 2: Divide the decimal by 4.
0.75 ÷ 4 = 0.1875
Step 3: Convert the decimal back to a fraction (optional).
While 0.1875 is a perfectly acceptable answer, converting it back to a fraction demonstrates the equivalence:
0.1875 can be written as 1875/10000. Simplifying this fraction by dividing both the numerator and denominator by 625 gives us 3/16. This confirms our previous answers.
The Mathematical Principles at Play
The reciprocal method is based on the fundamental principle of fraction division. Dividing by a number is equivalent to multiplying by its multiplicative inverse (reciprocal). This principle extends to all types of fractions and numbers. The reason this works lies in the definition of division itself. Division is essentially the inverse operation of multiplication.
When we say 3/4 ÷ 4, we are asking "What number, when multiplied by 4, equals 3/4?" Multiplying 3/16 by 4 gives us (3/16) x (4/1) = 12/16, which simplifies to 3/4. This confirms that 3/16 is the correct solution.
Common Misconceptions
A common mistake is to simply divide the numerator by the whole number and leave the denominator unchanged. This would incorrectly yield 3/4 ÷ 4 = 3/4. This is incorrect because it doesn't account for the division impacting the entire fraction. Remember, we're dividing the entire quantity 3/4, not just its numerator.
Frequently Asked Questions (FAQ)
Q: Can I divide the whole number by the numerator instead?
A: No. The order of division matters significantly in fraction division. You must divide the fraction by the whole number, not vice versa.
Q: What if the whole number was a fraction?
A: If the divisor was also a fraction (e.g., 3/4 ÷ 2/3), you would still use the reciprocal method. You would multiply 3/4 by the reciprocal of 2/3 (which is 3/2): (3/4) x (3/2) = 9/8.
Q: Is there a way to check my answer?
A: Yes. Multiply your answer (3/16) by the divisor (4). If you get the original dividend (3/4), your answer is correct. (3/16) x 4 = 12/16 = 3/4.
Q: Why is the reciprocal method used?
A: The reciprocal method is a shortcut that streamlines the process of dividing fractions. It's derived from the fundamental properties of multiplication and division.
Conclusion: Mastering Fraction Division
Dividing fractions, while initially appearing complex, is a manageable process with a clear and consistent methodology. By understanding the reciprocal method, applying visual aids, and exploring the underlying mathematical principles, we can confidently tackle problems like 3/4 divided by 4. The answer, 3/16, is not just a numerical result; it's a testament to a grasped understanding of fraction operations. Remember that practice is key to mastering this essential mathematical skill. The more you work with fractions, the more intuitive and straightforward this process will become. This detailed exploration provides a solid foundation for tackling more intricate fraction problems in the future. By understanding the why behind the methods, you'll build a stronger and more confident mathematical foundation.
Latest Posts
Latest Posts
-
45 Days From 1 9
Sep 11, 2025
-
Area Of Irregular Shape Calculator
Sep 11, 2025
-
Cuantos Mg Tiene Un Ml
Sep 11, 2025
-
Half Pints In A Gallon
Sep 11, 2025
-
1 6 Inch Diameter To Circumference
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 3 4 Divided By 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.