3 Percent Of 1 Million
wordexpert
Sep 07, 2025 · 6 min read
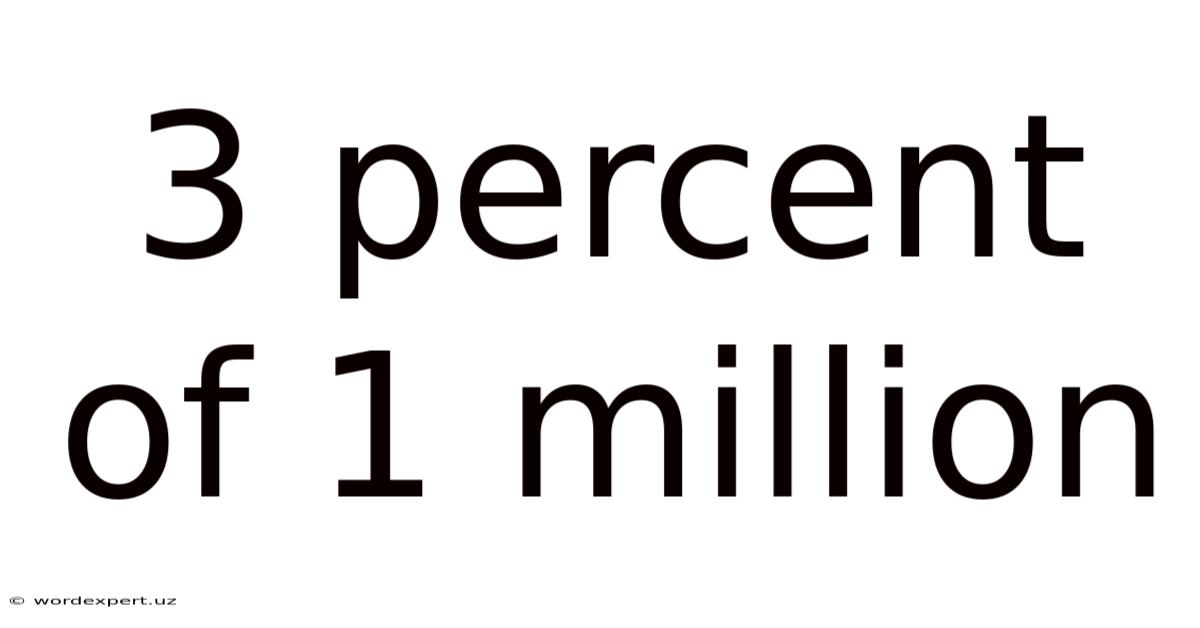
Table of Contents
Decoding 3 Percent of 1 Million: A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill applicable across various aspects of life, from everyday finances to complex scientific calculations. Understanding how to determine a percentage of a number, especially a large one like 1 million, is crucial for informed decision-making. This article will provide a comprehensive explanation of how to calculate 3 percent of 1 million, along with practical examples and explorations of the broader concept of percentages. We will delve into the methodology, explore its real-world applications, and address common questions surrounding percentage calculations.
Understanding Percentages: The Foundation
Before diving into the calculation of 3% of 1 million, let's establish a strong understanding of what a percentage represents. A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" is used to denote percentage. For instance, 10% means 10 out of 100, which can be written as a fraction (10/100) or a decimal (0.10). This fundamental understanding is key to solving any percentage problem.
Calculating 3% of 1 Million: The Methods
There are several ways to calculate 3% of 1 million. Each method offers a slightly different approach, catering to various levels of mathematical comfort.
Method 1: Using the Decimal Equivalent
This is perhaps the most straightforward method. First, convert the percentage to its decimal equivalent. To do this, divide the percentage by 100. In this case:
3% ÷ 100 = 0.03
Next, multiply this decimal by the number you want to find the percentage of (1 million):
0.03 x 1,000,000 = 30,000
Therefore, 3% of 1 million is 30,000.
Method 2: Using Fractions
Percentages can also be expressed as fractions. 3% can be written as 3/100. To find 3% of 1 million, multiply the fraction by 1 million:
(3/100) x 1,000,000 = 30,000
This method highlights the fractional nature of percentages, reinforcing the conceptual understanding. The calculation simplifies to 3 x 10,000 = 30,000, resulting in the same answer.
Method 3: Using Proportions
This method is particularly useful for understanding the relationship between the percentage, the whole, and the part. We can set up a proportion:
3/100 = x/1,000,000
Where 'x' represents the unknown value (3% of 1 million). To solve for x, cross-multiply:
100x = 3,000,000
Divide both sides by 100:
x = 30,000
This method provides a structured approach, particularly helpful when dealing with more complex percentage problems.
Real-World Applications: Where 3% of 1 Million Matters
The ability to calculate percentages like 3% of 1 million has extensive practical applications across various fields. Let's explore some examples:
-
Finance and Investment: Imagine a company with a net worth of $1 million. A 3% increase in its value would represent a gain of $30,000. Similarly, a 3% decrease would indicate a loss of $30,000. Understanding these calculations is vital for investors to track portfolio performance and make informed decisions.
-
Sales and Marketing: If a company makes $1 million in sales, a 3% commission paid to sales representatives would amount to $30,000. Similarly, calculating sales tax or discounts often involves percentage calculations.
-
Population Statistics: If a city has a population of 1 million, a 3% increase in population would represent an addition of 30,000 people. Analyzing population growth using percentages helps in urban planning and resource allocation.
-
Scientific Research: Percentage calculations are essential in analyzing experimental data. If an experiment involves 1 million trials, and 3% show a specific outcome, this translates to 30,000 instances. This is crucial for drawing conclusions and understanding statistical significance.
-
Data Analysis: In various fields, data is analyzed using percentages. Understanding how a specific subset contributes to a larger dataset is crucial for interpreting results and making informed decisions. For instance, analyzing customer satisfaction surveys, website traffic, or social media engagement often involves calculating percentages.
Beyond the Basics: Exploring More Complex Scenarios
While calculating 3% of 1 million is relatively straightforward, the underlying principles can be applied to much more complex scenarios. Consider these examples:
-
Calculating percentage change: This involves determining the percentage increase or decrease between two numbers. For instance, if a company's sales increase from $1 million to $1.05 million, the percentage change can be calculated as: [(1.05 million - 1 million) / 1 million] x 100% = 5%.
-
Compound interest: Compound interest involves earning interest on both the principal amount and accumulated interest. Understanding percentage calculations is crucial for computing compound interest over time.
-
Tax calculations: Calculating sales tax, income tax, or other forms of taxes involves applying a percentage to a base amount. Understanding these percentages is essential for accurate financial planning.
-
Statistical analysis: Many statistical measures, such as percentages, proportions, and rates, are based on percentage calculations. Understanding these concepts is essential for interpreting and analyzing data effectively.
Frequently Asked Questions (FAQ)
Q1: How do I calculate a different percentage of 1 million?
A1: Simply replace "3" in the equations above with the desired percentage. For example, to find 7% of 1 million, you would use 0.07 (or 7/100) instead of 0.03.
Q2: What if I need to find a percentage of a number other than 1 million?
A2: The methods described above apply to any number. Simply replace "1,000,000" with the desired number in the calculations.
Q3: Can I use a calculator for these calculations?
A3: Absolutely! Calculators simplify the process, especially for more complex percentage calculations. Most calculators have a percentage function (%) that can be used directly.
Q4: Are there online tools to calculate percentages?
A4: Yes, many online calculators and websites are specifically designed to calculate percentages. These tools can be particularly helpful for more complicated scenarios.
Q5: Why is understanding percentages important?
A5: Understanding percentages is essential for numerous applications in daily life, finance, science, and many other fields. It enables informed decision-making in various contexts, from personal budgeting to evaluating investment opportunities.
Conclusion: Mastering the Art of Percentage Calculation
Calculating 3% of 1 million, while seemingly a simple task, embodies the fundamental principles of percentage calculations. Understanding this concept allows us to navigate various real-world scenarios effectively. From financial planning to scientific analysis, mastering percentage calculations equips us with a critical skill for informed decision-making and a deeper understanding of numerical relationships. The methods described here provide a solid foundation for tackling a wide range of percentage problems, allowing for confident and accurate calculations in any context. Remember that practice is key to mastering this crucial skill, so don’t hesitate to try out different examples and solidify your understanding. The ability to work confidently with percentages opens doors to a more nuanced understanding of the world around us.
Latest Posts
Latest Posts
-
90 Days From March 13
Sep 11, 2025
-
What Is 0 05 In Percent
Sep 11, 2025
-
Flow Through An Orifice Calculator
Sep 11, 2025
-
Convert A Number To Millions
Sep 11, 2025
-
2 To The 10th Power
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 3 Percent Of 1 Million . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.