3 Percent Of 200 000
wordexpert
Sep 17, 2025 · 6 min read
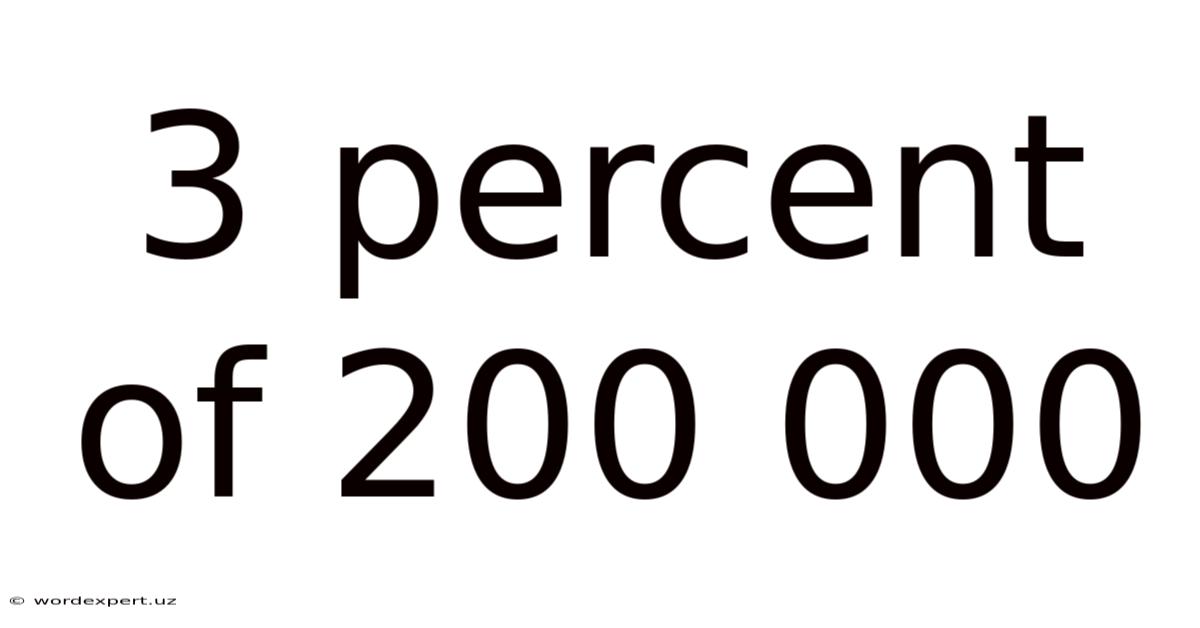
Table of Contents
Decoding 3 Percent of 200,000: A Deep Dive into Percentages and Their Applications
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex financial analysis and scientific research. Understanding how to determine a percentage of a larger number is crucial for informed decision-making. This article will thoroughly explore how to calculate 3% of 200,000, providing step-by-step instructions, explanations of the underlying mathematical principles, practical applications, and frequently asked questions. By the end, you’ll not only know the answer but also grasp the broader concept of percentages and their real-world significance.
Understanding Percentages
Before diving into the calculation, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per hundred" or "out of 100." For instance, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
To calculate a percentage of a number, we essentially find that fractional part of the whole number. This involves converting the percentage to a decimal or fraction and then multiplying it by the number.
Calculating 3% of 200,000: Step-by-Step Guide
There are two primary methods to calculate 3% of 200,000:
Method 1: Using Decimal Conversion
-
Convert the percentage to a decimal: To convert 3% to a decimal, divide it by 100: 3% ÷ 100 = 0.03
-
Multiply the decimal by the number: Multiply the decimal (0.03) by 200,000: 0.03 × 200,000 = 6,000
Therefore, 3% of 200,000 is 6,000.
Method 2: Using Fraction Conversion
-
Convert the percentage to a fraction: 3% can be written as the fraction 3/100.
-
Multiply the fraction by the number: Multiply the fraction (3/100) by 200,000: (3/100) × 200,000 = 6,000
Again, the result is 6,000. Both methods yield the same answer, highlighting the interchangeability of decimals and fractions in percentage calculations.
Practical Applications: Where Percentages Matter
The ability to calculate percentages has far-reaching practical implications in various aspects of life:
-
Finance: Calculating interest on loans, mortgages, and savings accounts; determining tax rates and amounts; analyzing investment returns; understanding discount percentages in sales. For example, a 3% interest rate on a $200,000 loan would mean an annual interest payment of $6,000 (as we've calculated).
-
Business: Analyzing profit margins; calculating sales growth; determining market share; assessing the effectiveness of marketing campaigns; understanding cost increases and decreases. A company might analyze that 3% of their 200,000 customer base (6,000 customers) are responsible for 50% of their total sales revenue, allowing them to tailor marketing strategies.
-
Science: Expressing experimental results; calculating error margins; representing data in graphs and charts; determining statistical significance; analyzing population changes or growth rates. Researchers might find that 3% of a 200,000 sample size showed a specific reaction to a treatment.
-
Everyday Life: Calculating tips in restaurants; determining discounts on purchases; understanding sales tax; budgeting expenses; tracking savings progress. Many people use percentage calculations unconsciously - for example, quickly calculating a 15% tip on a restaurant bill.
-
Data Analysis: Understanding proportions and distributions within large datasets. In market research, for example, identifying 3% of a respondent group (6,000 out of 200,000) with a particular preference can have significant implications for product development.
Beyond the Basics: Expanding Percentage Calculations
While we've focused on calculating 3% of 200,000, the underlying principles can be extended to any percentage and any number. The fundamental steps remain the same: convert the percentage to a decimal or fraction, and then multiply it by the number.
Let's consider some variations:
-
Calculating X% of 200,000: To calculate any percentage (X%) of 200,000, simply replace '3' with 'X' in the above equations. The formula would be: (X/100) * 200,000
-
Calculating 3% of Y: To calculate 3% of any number (Y), replace '200,000' with 'Y': 0.03 * Y
-
Finding the Percentage One Number Represents of Another: To determine what percentage one number (A) represents of another number (B), divide A by B, and then multiply the result by 100. For example, to find what percentage 6,000 is of 200,000: (6,000/200,000) * 100 = 3%
Scientific Explanation: Proportional Reasoning
At its core, percentage calculation hinges on the concept of proportional reasoning. This is a fundamental mathematical principle that deals with relationships between quantities. In percentage calculations, we're determining a proportional relationship between a part (the percentage) and a whole (the total number).
The formula we implicitly used can be expressed more formally as:
Part = Percentage × Whole
Where:
Partis the result of the percentage calculation (in our case, 6,000)Percentageis the percentage expressed as a decimal or fraction (0.03 or 3/100)Wholeis the total number (200,000)
Understanding proportional reasoning allows us to not only calculate percentages but also solve for unknown variables in various proportional relationships.
Frequently Asked Questions (FAQs)
Q1: What if I need to calculate a percentage that includes decimals, such as 3.5% of 200,000?
A1: The process remains the same. Convert 3.5% to a decimal (0.035) and multiply it by 200,000: 0.035 × 200,000 = 7,000.
Q2: How can I calculate the percentage increase or decrease between two numbers?
A2: To calculate the percentage increase, subtract the original number from the new number, divide the result by the original number, and then multiply by 100. For percentage decrease, follow the same steps but subtract the new number from the original number.
Q3: Are there any online calculators or tools that can help with percentage calculations?
A3: Yes, many online calculators are readily available to perform these calculations. However, understanding the underlying principles is crucial for applying these calculations effectively in diverse scenarios.
Q4: What are some common errors to avoid when calculating percentages?
A4: Common errors include incorrect decimal conversions, using the wrong formula, and misunderstanding the context of the problem. Always double-check your work and ensure you're using the correct numbers and operations.
Conclusion: Mastering the Power of Percentages
Calculating 3% of 200,000, resulting in 6,000, is a straightforward yet powerful illustration of the significance of understanding percentages. This skill is essential for navigating numerous aspects of personal finance, business decisions, scientific analysis, and everyday life. By grasping the underlying mathematical principles and mastering the various calculation methods, you'll be equipped to tackle a wide range of percentage-related problems with confidence. Remember that consistent practice and a clear understanding of the concepts are key to mastering this fundamental skill. The ability to work comfortably with percentages will significantly enhance your quantitative reasoning abilities and equip you to make informed decisions based on numerical data.
Latest Posts
Latest Posts
-
12 Weeks From August 1
Sep 17, 2025
-
How To Calculate Fev1 Fvc Ratio
Sep 17, 2025
-
What Is A 8 10 Grade
Sep 17, 2025
-
8 Fluid Ounces To Ml
Sep 17, 2025
-
10 1 Compression Ratio To Psi
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 3 Percent Of 200 000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.