3 Percent Of 3 Million
wordexpert
Sep 10, 2025 · 5 min read
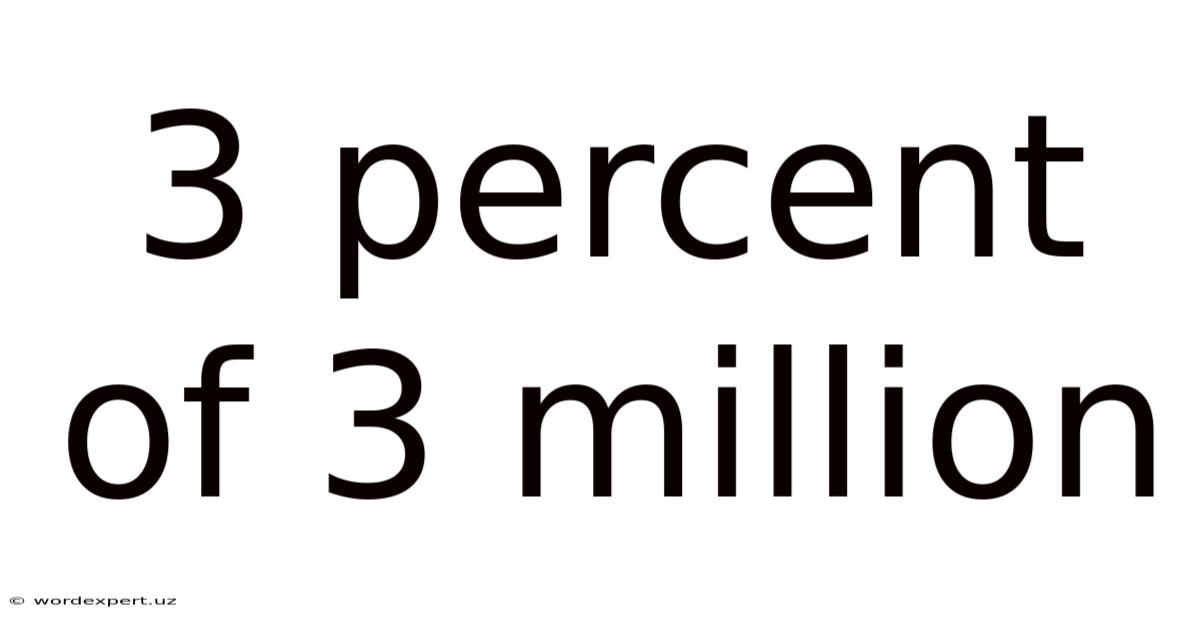
Table of Contents
Decoding 3 Percent of 3 Million: A Comprehensive Guide
Finding 3 percent of 3 million might seem like a simple calculation, but understanding the underlying principles and applications of percentages extends far beyond this specific problem. This article will delve into the calculation itself, explore various methods for solving percentage problems, examine real-world applications, and address common misconceptions surrounding percentages. We'll also explore the broader mathematical concepts involved, making this a comprehensive guide suitable for anyone from students to professionals.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The term "percent" comes from the Latin "per centum," meaning "out of one hundred." So, 3 percent means 3 out of every 100. This fundamental understanding is crucial for tackling any percentage problem, including calculating 3 percent of 3 million.
Method 1: The Direct Calculation Method
The most straightforward way to calculate 3 percent of 3 million is to convert the percentage to a decimal and then multiply.
-
Step 1: Convert the percentage to a decimal. To do this, divide the percentage by 100. So, 3 percent becomes 3/100 = 0.03.
-
Step 2: Multiply the decimal by the total amount. In this case, we multiply 0.03 by 3,000,000. This gives us: 0.03 * 3,000,000 = 90,000.
Therefore, 3 percent of 3 million is $\boxed{90,000}$.
Method 2: The Fraction Method
Percentages can also be expressed as fractions. 3 percent can be written as 3/100. To calculate 3 percent of 3 million using this method:
-
Step 1: Represent the percentage as a fraction: 3% = 3/100
-
Step 2: Multiply the fraction by the total amount: (3/100) * 3,000,000
-
Step 3: Simplify the expression: This simplifies to (3 * 3,000,000) / 100 = 9,000,000 / 100 = 90,000.
Again, we arrive at the answer: $\boxed{90,000}$.
Method 3: Using Proportions
The proportion method provides a more intuitive understanding of the calculation. We can set up a proportion:
-
Step 1: Set up the proportion: Let 'x' represent 3 percent of 3 million. We can write this as: x/3,000,000 = 3/100
-
Step 2: Cross-multiply: 100x = 3 * 3,000,000 = 9,000,000
-
Step 3: Solve for x: x = 9,000,000 / 100 = 90,000
This method reinforces the concept that a percentage is a ratio and provides a structured approach to solving percentage problems.
Real-World Applications: Where Percentages Matter
Understanding how to calculate percentages is crucial in numerous real-world scenarios:
-
Finance: Calculating interest on loans, investments, and savings accounts relies heavily on percentage calculations. Understanding compound interest, for example, involves repeated percentage calculations. Calculating taxes, discounts, and profit margins all necessitate proficiency in percentage calculations.
-
Business: Analyzing sales data, market share, and profit margins requires calculating percentages. Businesses use percentages to track their performance, identify trends, and make informed decisions. Understanding percentage change (increase or decrease) is vital for business planning and forecasting.
-
Science: Percentages are used extensively in scientific research to represent data, express error margins, and calculate concentrations of solutions. Statistical analysis relies heavily on percentages and proportions.
-
Everyday Life: Calculating tips at restaurants, understanding sales discounts, and interpreting statistics presented in news reports all involve using percentages.
Beyond the Basics: More Complex Percentage Problems
While calculating 3 percent of 3 million is relatively straightforward, percentage problems can become more complex. Consider these examples:
-
Finding the Percentage: What percentage of 5 million is 150,000? This involves dividing 150,000 by 5,000,000 and multiplying by 100 to get the percentage.
-
Finding the Original Amount: If 10 percent of a certain amount is 200, what is the original amount? This involves setting up an equation: 0.10 * x = 200, and solving for x.
-
Percentage Increase/Decrease: If a value increases from 100 to 120, what is the percentage increase? This involves calculating the difference (20), dividing it by the original value (100), and multiplying by 100 to express it as a percentage.
Common Misconceptions about Percentages
Several common misconceptions can lead to errors in percentage calculations:
-
Confusing percentage increase/decrease: A 10% increase followed by a 10% decrease does not result in the original value.
-
Incorrect order of operations: When dealing with multiple percentage calculations, it's essential to follow the correct order of operations (PEMDAS/BODMAS).
-
Misinterpreting percentages: Always carefully read the context in which a percentage is presented to ensure correct interpretation.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve percentage problems? A: Yes, calculators are a valuable tool for solving percentage problems, especially for larger numbers or more complex calculations.
-
Q: Are there any online tools or websites that can help with percentage calculations? A: Yes, many websites and online calculators are available specifically designed for percentage calculations.
-
Q: What are some common mistakes to avoid when calculating percentages? A: Avoid rounding off intermediate results too early, and always double-check your calculations, especially when dealing with multiple percentage operations.
Conclusion:
Calculating 3 percent of 3 million, while seemingly simple, provides a gateway to understanding the broader world of percentage calculations. Mastering this fundamental concept opens doors to a deeper understanding of finance, business, science, and everyday life. By understanding the different methods—direct calculation, fraction method, and proportions—and by avoiding common misconceptions, you can confidently tackle any percentage problem you encounter. Remember, the key is understanding the underlying principles and applying them systematically. This detailed explanation aims not only to provide the answer but also to equip you with the knowledge and confidence to handle similar calculations and more complex percentage problems independently.
Latest Posts
Latest Posts
-
26 Mpg To L 100km
Sep 10, 2025
-
How Long Till 3 10
Sep 10, 2025
-
Ski Binding Din Setting Calculator
Sep 10, 2025
-
Convert Milligrams To Milliliters Chart
Sep 10, 2025
-
Board Foot Calculator For Logs
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 3 Percent Of 3 Million . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.