30 Percent Off Of 150
wordexpert
Sep 18, 2025 · 5 min read
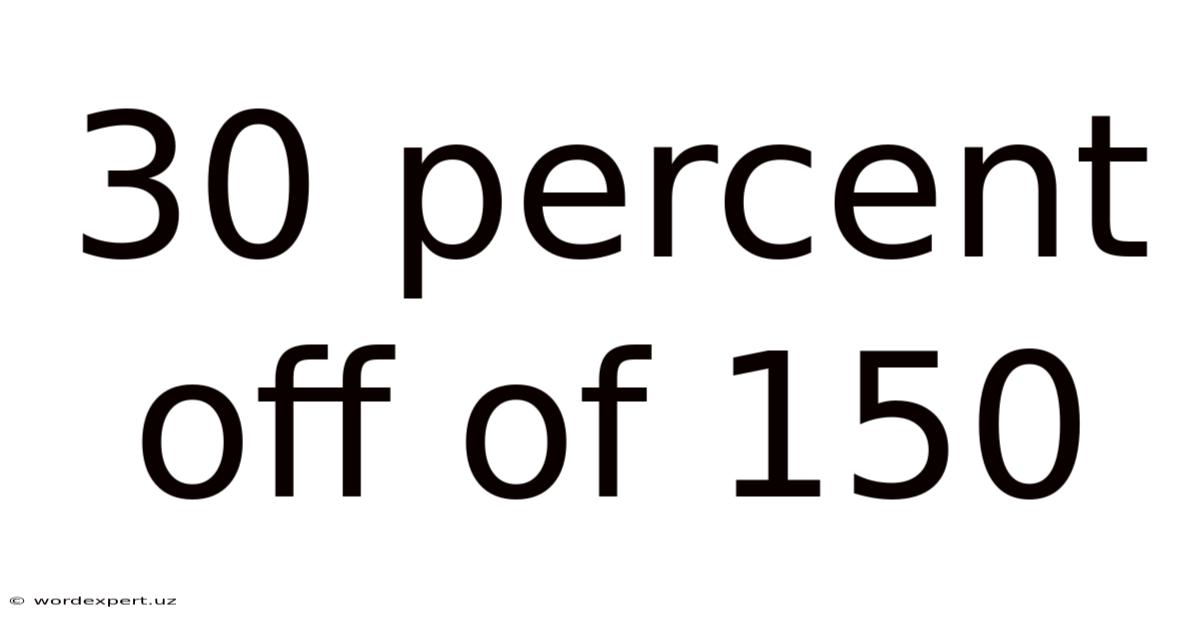
Table of Contents
Calculating 30% Off of $150: A Comprehensive Guide
Finding a 30% discount on a $150 item is a common scenario, whether you're shopping online, browsing in-store sales, or simply working through a personal finance problem. Understanding how to calculate this discount quickly and accurately is a valuable skill. This article will guide you through several methods to determine the final price, explaining the underlying math in a clear and accessible way. We'll also cover related concepts to enhance your understanding of percentages and discounts. This will equip you with the knowledge to confidently tackle similar problems in the future.
Understanding Percentages and Discounts
Before diving into the calculation, let's briefly review the fundamentals. A percentage is a fraction of 100. For example, 30% means 30 out of 100, or 30/100, which simplifies to 3/10. A discount is a reduction in the original price of an item. In this case, we're dealing with a 30% discount on a $150 item. This means we need to find 30% of $150 and then subtract that amount from the original price to determine the final cost.
Method 1: Calculating the Discount Directly
This is the most straightforward approach. We'll first calculate 30% of $150 and then subtract that value from the original price.
-
Convert the percentage to a decimal: To do this, divide the percentage by 100. So, 30% becomes 30/100 = 0.30.
-
Multiply the decimal by the original price: Multiply 0.30 by $150: 0.30 x $150 = $45. This represents the amount of the discount.
-
Subtract the discount from the original price: Subtract the discount ($45) from the original price ($150): $150 - $45 = $105.
Therefore, the final price after a 30% discount on a $150 item is $\boxed{$105}$.
Method 2: Finding the Remaining Percentage
This method focuses on calculating the percentage of the original price that remains after the discount. Since we have a 30% discount, this means 70% (100% - 30%) of the original price remains.
-
Calculate the remaining percentage: 100% - 30% = 70%.
-
Convert the remaining percentage to a decimal: 70% becomes 70/100 = 0.70.
-
Multiply the decimal by the original price: Multiply 0.70 by $150: 0.70 x $150 = $105.
This directly gives us the final price after the discount, which is $\boxed{$105}$. This method can be particularly useful when dealing with multiple discounts or complex scenarios.
Method 3: Using Fractions
Percentages can also be expressed as fractions. 30% is equivalent to the fraction 30/100, which simplifies to 3/10.
-
Express the percentage as a fraction: 30% = 30/100 = 3/10.
-
Multiply the fraction by the original price: Multiply 3/10 by $150: (3/10) x $150 = $45. This is the discount amount.
-
Subtract the discount from the original price: $150 - $45 = $105.
The final price after the discount is $\boxed{$105}$. While this method is accurate, it might be slightly less intuitive for those less comfortable with fractions.
Method 4: Mental Math Techniques (Approximation)
For quick estimations, mental math techniques can be helpful, although they might not provide the exact answer.
-
Rounding: Round the original price to a more manageable number. In this case, $150 is already relatively easy to work with.
-
Calculating 10%: Finding 10% of a number is simple; just move the decimal point one place to the left. 10% of $150 is $15.
-
Scaling: Since 30% is three times 10%, multiply the 10% value by 3: $15 x 3 = $45. This is an approximation of the discount.
-
Subtracting: Subtract the approximate discount from the original price: $150 - $45 = $105. This gives a very close approximation to the actual discounted price.
This method is useful for quick estimations, but for accuracy, it is always best to use one of the previous methods.
Understanding the Concept of "Sale Price"
The final price after applying the discount ($105) is often referred to as the sale price. This is the amount you would pay for the item after the discount has been applied.
Practical Applications and Real-World Scenarios
Understanding how to calculate discounts is crucial in many real-world situations:
- Shopping: Determining the final price of sale items is essential for budget management.
- Finance: Calculating discounts on investments or loans is crucial for understanding financial gains or savings.
- Negotiations: Knowing how to calculate discounts can be a valuable skill during price negotiations.
- Education: Understanding percentages is a fundamental mathematical skill with broader applications in various fields.
Frequently Asked Questions (FAQs)
- Q: What if the discount is a different percentage?
A: Follow the same methods outlined above, substituting the new percentage for 30%. For example, for a 25% discount, you would calculate 25% of $150 and subtract the result from $150.
- Q: How do I calculate the discount if the original price is different?
A: Replace $150 with the new original price in any of the methods described above. The process remains the same; simply substitute the new value.
- Q: Can I use a calculator for this?
A: Yes, a calculator can significantly simplify the process, especially for larger numbers or more complex discount calculations. Most calculators have a percentage function (%) which can be utilized directly.
- Q: What if there are multiple discounts?
A: With multiple discounts, you apply them sequentially. Calculate the first discount, then apply the second discount to the resulting price, and so on. It is important to note that the order in which discounts are applied can affect the final price.
Conclusion
Calculating a 30% discount on $150, resulting in a final price of $105, is a fundamental skill applicable in numerous contexts. We've explored several methods—direct calculation, finding the remaining percentage, using fractions, and mental math approximations—providing a comprehensive understanding of the underlying principles. Mastering these techniques empowers you to confidently handle discounts and percentages in your daily life, making you a more informed and savvy consumer. Remember to choose the method that best suits your comfort level and the specific situation. Regardless of the approach, the core principle remains the same: understanding the relationship between percentages, decimals, and fractions to efficiently determine the final price after a discount.
Latest Posts
Latest Posts
-
How Much Is 13 Ounces
Sep 18, 2025
-
Area Of A Oval Calculator
Sep 18, 2025
-
How Long Is 250 Seconds
Sep 18, 2025
-
180 Degrees Celsius To Fahrenheit
Sep 18, 2025
-
Labor Force Participation Rate Calculation
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 30 Percent Off Of 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.