30 Percent Off Of 45
wordexpert
Sep 19, 2025 · 5 min read
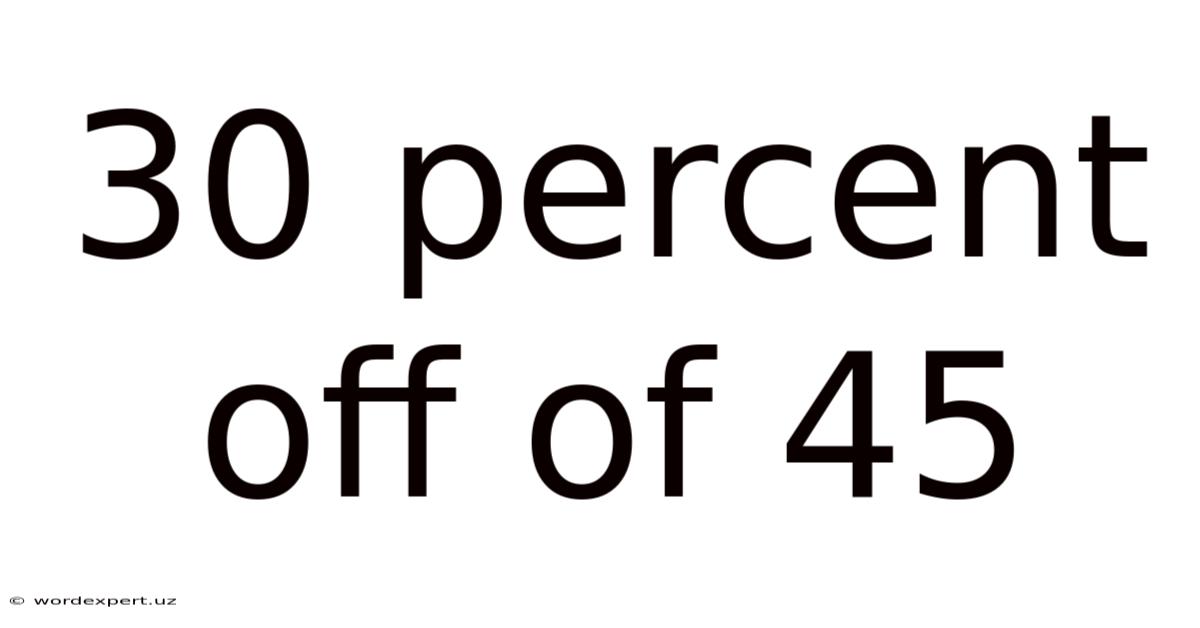
Table of Contents
Calculating 30% Off of 45: A Comprehensive Guide
Finding a 30% discount on a $45 item might seem straightforward, but understanding the underlying math can be surprisingly useful in various everyday situations, from shopping to budgeting. This comprehensive guide will walk you through different methods of calculating this discount, explain the underlying principles, and explore practical applications. We'll cover everything from basic percentage calculations to more advanced techniques, ensuring you become confident in tackling similar problems. Understanding discounts is a crucial life skill, and this article will equip you with the knowledge to master it.
Understanding Percentages
Before diving into the calculation, let's refresh our understanding of percentages. A percentage is a fraction expressed as a part of 100. For example, 30% means 30 out of 100, which can be written as the fraction 30/100 or the decimal 0.30. This representation is crucial for performing calculations.
Method 1: Finding 30% of 45 Directly
The most straightforward method involves directly calculating 30% of 45. We can do this by converting the percentage to a decimal and multiplying it by the original price:
- Convert the percentage to a decimal: 30% = 0.30
- Multiply the decimal by the original price: 0.30 x $45 = $13.50
This calculation shows that a 30% discount on a $45 item is $13.50.
Method 2: Finding the Remaining Percentage
Instead of directly calculating the discount, we can determine the remaining percentage after the discount is applied. If we have a 30% discount, then 100% - 30% = 70% of the original price remains. We can then calculate this remaining percentage:
- Calculate the remaining percentage: 100% - 30% = 70%
- Convert the remaining percentage to a decimal: 70% = 0.70
- Multiply the decimal by the original price: 0.70 x $45 = $31.50
This shows that after a 30% discount, the final price will be $31.50. This method is useful when you want to quickly determine the final price without calculating the discount amount separately.
Method 3: Using Fractions
Percentages can also be expressed as fractions. 30% is equivalent to 30/100, which can be simplified to 3/10. We can use this fraction to calculate the discount:
- Express the percentage as a fraction: 30% = 30/100 = 3/10
- Multiply the fraction by the original price: (3/10) x $45 = $13.50
This confirms that the discount amount is $13.50. This method provides an alternative approach to calculating the discount.
Practical Applications and Real-World Scenarios
Understanding percentage discounts isn't just about solving mathematical problems; it's a crucial skill for navigating everyday financial decisions. Here are some real-world scenarios where this knowledge comes in handy:
-
Shopping: When you see a sale advertised as "30% off," you can quickly determine the actual savings and the final price of an item. This empowers you to make informed purchasing decisions and stick to your budget.
-
Sales Tax Calculation: Many countries apply sales tax to purchases. After calculating the discount, you'll need to add the sales tax to determine the final price you'll pay. For example, if the sales tax is 5%, you would calculate 5% of $31.50 (the price after the discount) and add it to the discounted price.
-
Investment Returns: Understanding percentage changes is essential when tracking investment returns. If your investment grows by 30%, you can apply similar calculation methods to determine the exact increase in value.
-
Budgeting and Savings: Tracking your savings and expenses often involves calculating percentages. For instance, you might want to determine what percentage of your income you're saving or spending on certain categories.
-
Tip Calculation: Calculating tips in restaurants often involves determining a percentage of the total bill. Knowing how to calculate percentages quickly and accurately ensures you leave a fair tip without excessive mental calculation.
Advanced Applications: Compound Discounts and Multiple Discounts
While the example focuses on a single discount, real-world situations can involve multiple discounts or compound discounts (discount applied to a discounted price). Understanding these scenarios requires a slightly different approach.
-
Multiple Discounts: If you have multiple discounts, you apply them sequentially. For instance, if you have a 30% discount followed by a 10% discount, you apply the 30% discount first, and then apply the 10% discount to the resulting price. This is different than simply adding the percentages together (30% + 10% = 40%).
-
Compound Discounts: Compound discounts occur when a discount is applied to a price that has already been discounted. This means that the subsequent discount is calculated on a lower base price.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate a 30% discount?
A: The easiest way is to convert 30% to a decimal (0.30) and multiply it by the original price ($45). This gives you the discount amount directly.
Q: How do I calculate the final price after a 30% discount?
A: You can either subtract the discount amount from the original price or calculate 70% (100% - 30%) of the original price directly.
Q: Can I use a calculator to calculate percentage discounts?
A: Yes, calculators are very useful for these calculations. Most calculators have a percentage function that simplifies the process.
Q: What if the discount isn't a whole number percentage (e.g., 27.5%)?
A: The process remains the same. Convert the percentage to a decimal (27.5% = 0.275) and multiply by the original price.
Q: What if I have multiple discounts or a compound discount?
A: For multiple discounts, apply them sequentially. For compound discounts, apply the second discount to the already discounted price. Do not simply add the percentages.
Q: Are there any online tools to help calculate percentage discounts?
A: Yes, many websites and apps provide percentage calculators that can handle various discount scenarios, including multiple and compound discounts. These can be extremely helpful for complex situations.
Conclusion: Mastering Percentage Calculations
Calculating a 30% discount on $45, or any percentage discount for that matter, is a fundamental skill applicable across numerous life situations. By understanding the different methods – direct calculation, remaining percentage calculation, and fractional methods – you build a strong foundation for managing your finances and making informed decisions. Remember to practice these methods regularly, and you'll soon find yourself confidently tackling percentage calculations in various contexts, from shopping to investing and beyond. The ability to swiftly and accurately calculate percentages is a valuable asset that enhances financial literacy and empowers better decision-making in everyday life.
Latest Posts
Latest Posts
-
How Much Does Concrete Way
Sep 19, 2025
-
600 Square Meter To Feet
Sep 19, 2025
-
When Was 26 Weeks Ago
Sep 19, 2025
-
How To Find Square Yards
Sep 19, 2025
-
3 Million Seconds To Days
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 30 Percent Off Of 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.