38 50 As A Percent
wordexpert
Sep 21, 2025 · 6 min read
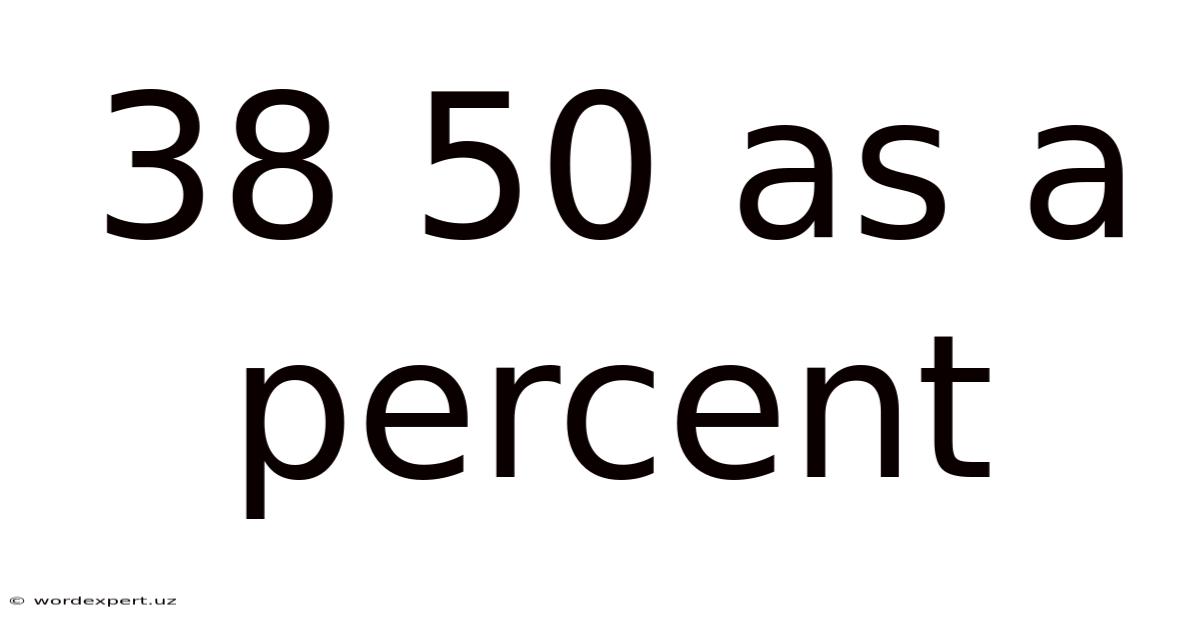
Table of Contents
Understanding 38/50 as a Percentage: A Comprehensive Guide
This article will delve into the conversion of the fraction 38/50 into a percentage, exploring various methods and providing a solid understanding of the underlying concepts. We'll also discuss practical applications and address frequently asked questions, making this a comprehensive resource for anyone needing to understand percentage calculations. The key concept here revolves around understanding fractions, decimals, and percentages and their interchangeable nature.
Introduction: Fractions, Decimals, and Percentages – An Interconnected Trio
Before diving into the specific calculation of 38/50 as a percentage, let's establish a firm grasp on the fundamental relationship between fractions, decimals, and percentages. These three represent different ways of expressing the same numerical value. A fraction shows a part of a whole using a numerator (top number) and a denominator (bottom number). A decimal represents a fraction where the denominator is a power of 10. A percentage represents a fraction where the denominator is 100. Understanding this interconnectedness is crucial for smoothly converting between these forms.
Method 1: Direct Conversion using the Formula
The most straightforward method to convert a fraction to a percentage involves a simple formula:
(Numerator / Denominator) x 100%
In our case, the fraction is 38/50. Applying the formula:
(38 / 50) x 100% = 0.76 x 100% = 76%
Therefore, 38/50 is equivalent to 76%.
Method 2: Simplifying the Fraction First
Often, simplifying the fraction before conversion can make the calculation easier. This involves finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. The GCD of 38 and 50 is 2. Simplifying the fraction:
38 ÷ 2 = 19 50 ÷ 2 = 25
This simplifies the fraction to 19/25. Now, we can apply the percentage formula:
(19 / 25) x 100% = 0.76 x 100% = 76%
As expected, we arrive at the same result: 76%. This method showcases that simplifying the fraction doesn't alter the final percentage.
Method 3: Decimal Conversion as an Intermediate Step
Another approach involves converting the fraction to a decimal first and then converting the decimal to a percentage. To convert 38/50 to a decimal, we simply divide the numerator by the denominator:
38 ÷ 50 = 0.76
To convert a decimal to a percentage, we multiply by 100%:
0.76 x 100% = 76%
Again, we obtain the same result: 76%. This method is particularly useful when dealing with fractions that are difficult to simplify mentally.
Practical Applications of Percentage Calculations
Understanding how to convert fractions to percentages is vital in many real-world scenarios. Here are some examples:
- Academic Performance: If a student answers 38 out of 50 questions correctly on a test, their score is 76%.
- Sales and Discounts: A store offering a 24% discount on an item initially priced at $50 would reduce the price by (24/100) x $50 = $12. The new price would be $50 - $12 = $38. This demonstrates the reverse calculation—finding the original amount given a percentage.
- Financial Calculations: Percentage calculations are fundamental in finance, including interest rates, loan repayments, and investment returns. For example, calculating the interest earned on a savings account or understanding the percentage increase in a stock's value relies heavily on these calculations.
- Data Analysis and Statistics: Percentages are widely used to represent proportions and trends in data analysis. For example, representing survey results, market share, or population demographics frequently involves percentages.
- Everyday Life: Many everyday situations involve percentages, such as calculating tips in restaurants, understanding sales tax, or figuring out the percentage of ingredients in a recipe.
Understanding the Concept of Percentage Increase and Decrease
While we've focused on converting a fraction to a percentage, it's important to understand related concepts. Let's consider scenarios involving percentage increases and decreases.
Percentage Increase: If a quantity increases from an initial value to a new value, the percentage increase is calculated as:
[(New Value - Initial Value) / Initial Value] x 100%
Percentage Decrease: If a quantity decreases from an initial value to a new value, the percentage decrease is calculated as:
[(Initial Value - New Value) / Initial Value] x 100%
Let's illustrate this with examples:
-
Scenario 1 (Increase): Suppose the price of a product increases from $50 to $58. The percentage increase is [(58-50)/50] x 100% = 16%
-
Scenario 2 (Decrease): Suppose the number of students in a class decreases from 50 to 38. The percentage decrease is [(50-38)/50] x 100% = 24%
These examples highlight how percentage changes are calculated and interpreted in practical situations.
Scientific Explanation: The Ratio and Proportion Concept
From a scientific standpoint, the conversion of 38/50 to a percentage is based on the fundamental concept of ratios and proportions. A ratio compares two quantities, while a proportion establishes an equivalence between two ratios. In our case, the ratio 38:50 is equivalent to the proportion x:100, where x is the percentage we are trying to find. Solving this proportion gives us:
38/50 = x/100
Cross-multiplying and solving for x:
50x = 3800 x = 76
Therefore, the percentage is 76%. This approach demonstrates the mathematical underpinning of percentage calculations.
Frequently Asked Questions (FAQ)
Q1: What if the denominator is not a multiple of 100?
A: Even if the denominator isn't a multiple of 100, you can still use the formula (Numerator / Denominator) x 100%. The result may be a decimal percentage, which is perfectly acceptable.
Q2: How do I convert a percentage back to a fraction?
A: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 76% becomes 76/100, which simplifies to 19/25.
Q3: Are there any online calculators to help with these conversions?
A: Yes, many online calculators are available that can perform fraction-to-percentage conversions quickly and accurately. However, understanding the underlying process is crucial for problem-solving and avoids over-reliance on technology.
Q4: How can I improve my understanding of percentages?
A: Practice is key! Try working through different examples, using various methods, and tackling problems that involve percentage increases and decreases. The more you practice, the more comfortable you will become with these calculations.
Conclusion: Mastering Percentage Calculations
Converting 38/50 to a percentage is a fundamental skill applicable across numerous fields. We’ve explored multiple methods—direct conversion, simplifying the fraction, and using a decimal as an intermediary—each illustrating the interconnectedness of fractions, decimals, and percentages. By grasping these concepts and applying them to practical scenarios, you can build a strong foundation for tackling more complex percentage-related problems and confidently navigate situations requiring these calculations in your academic, professional, and personal life. Remember that the key to mastery is practice and a thorough understanding of the underlying principles.
Latest Posts
Latest Posts
-
Inch Lb To Ft Lbs
Sep 21, 2025
-
90 Days After April 25
Sep 21, 2025
-
How To Calculate Ballistic Coefficient
Sep 21, 2025
-
20 Hours In A Day
Sep 21, 2025
-
How Long Is Two Decades
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 38 50 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.