5 7 As A Percent
wordexpert
Sep 14, 2025 · 5 min read
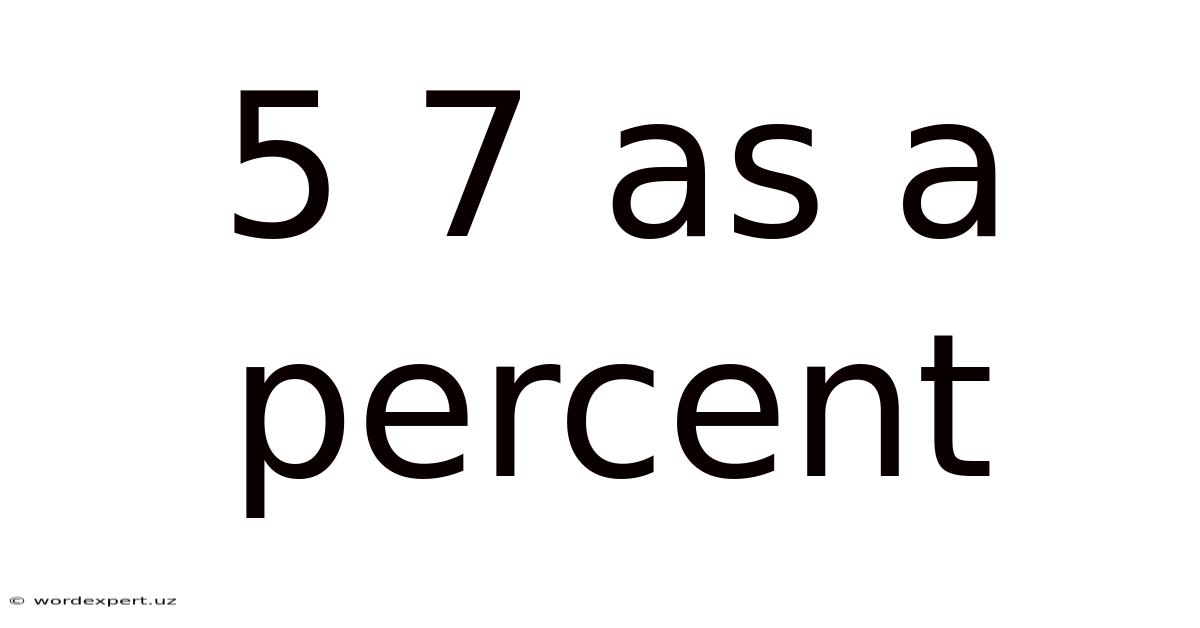
Table of Contents
Decoding 5/7 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics, crucial for various applications in everyday life, from calculating discounts to understanding financial reports. This comprehensive guide delves into the conversion of the fraction 5/7 into a percentage, explaining the process step-by-step, exploring the underlying mathematical principles, and addressing common questions. We'll also look at practical applications and related concepts to build a strong foundational understanding.
Introduction: Understanding Fractions and Percentages
A fraction represents a part of a whole. The fraction 5/7 indicates 5 parts out of a total of 7 equal parts. A percentage, on the other hand, expresses a fraction as a portion of 100. Converting a fraction to a percentage involves finding the equivalent fraction with a denominator of 100. This allows for easy comparison and interpretation of different proportions. The process of converting 5/7 to a percentage will involve division and multiplication, ultimately giving us a clear representation of the fraction as a percentage.
Step-by-Step Conversion: Turning 5/7 into a Percentage
The most straightforward method to convert 5/7 into a percentage involves two simple steps:
-
Division: Divide the numerator (5) by the denominator (7). This gives us a decimal value.
5 ÷ 7 ≈ 0.7142857
-
Multiplication: Multiply the decimal value obtained in step 1 by 100 to express it as a percentage.
0.7142857 × 100 ≈ 71.42857%
Therefore, 5/7 is approximately equal to 71.43% when rounded to two decimal places.
Mathematical Explanation: The Logic Behind the Conversion
The conversion process is based on the fundamental principle of equivalent fractions. Any fraction can be expressed in infinitely many equivalent forms by multiplying or dividing both the numerator and the denominator by the same non-zero number. The key to converting to a percentage is to find an equivalent fraction with a denominator of 100.
While we can't directly obtain a fraction with a denominator of 100 from 5/7 (since 7 doesn't divide evenly into 100), the division step effectively finds the decimal equivalent. This decimal represents the proportion of the whole that 5/7 represents. Multiplying by 100 then scales this proportion to express it as parts per hundred, which is the definition of a percentage.
Understanding the Remainder and Rounding
Notice that the decimal value of 5/7 (0.7142857...) is a non-terminating decimal. This means it goes on forever without repeating in a predictable pattern. This is because 7 is a prime number that doesn't divide evenly into powers of 10.
In practical applications, we often round the percentage to a convenient number of decimal places. Rounding to two decimal places, as we did above, gives us 71.43%. The level of precision required will depend on the context. For some calculations, a rough estimate might suffice, while in other situations, greater accuracy is necessary. Understanding the limitations of rounding is crucial for interpreting results correctly.
Practical Applications of Percentage Conversions
Converting fractions to percentages has wide-ranging applications in various fields:
- Finance: Calculating interest rates, discounts, profit margins, and tax rates all rely on understanding percentages.
- Statistics: Percentages are commonly used to represent proportions and probabilities in data analysis.
- Science: Representing experimental results, concentrations of solutions, and changes in quantities often utilizes percentages.
- Everyday Life: Calculating tips in restaurants, understanding sale prices, and interpreting survey results all involve working with percentages.
Illustrative Examples:
Let's consider a few practical examples to solidify our understanding:
-
Example 1: Test Scores: If a student answers 5 out of 7 questions correctly on a test, their score is approximately 71.43%. This provides a clear representation of their performance compared to the total number of questions.
-
Example 2: Sales Discount: A store offers a discount of 5/7 on an item. This means the customer receives a discount of approximately 71.43% on the original price.
-
Example 3: Survey Results: In a survey of 7 people, 5 prefer a particular brand. The percentage of people preferring that brand is approximately 71.43%.
Frequently Asked Questions (FAQs)
-
Q: Is there a way to convert 5/7 to a percentage without using a calculator?
A: While a calculator simplifies the process, you can perform long division to find the decimal equivalent of 5/7, and then multiply by 100. This is a more time-consuming method but demonstrates the underlying mathematical principles.
-
Q: What is the exact percentage value of 5/7?
A: The exact value is a non-terminating decimal, expressed as 71.42857142857...%. It cannot be expressed precisely as a finite decimal.
-
Q: How do I choose the appropriate number of decimal places when rounding?
A: The number of decimal places depends on the required level of accuracy. In most cases, rounding to two decimal places is sufficient. However, for higher precision, you may need more decimal places. The context dictates the level of precision needed.
-
Q: Are there other methods to convert fractions to percentages?
A: Yes, some fractions can be converted by finding an equivalent fraction with a denominator of 100. However, this method isn't always practical, especially for fractions with prime denominators. The division-multiplication method is generally the most efficient and widely applicable approach.
Conclusion: Mastering Percentage Conversions
Converting fractions like 5/7 to percentages is a crucial skill in mathematics and its applications. Understanding the underlying principles of equivalent fractions and decimal representation allows you to approach such conversions with confidence. The step-by-step process, explained thoroughly in this guide, provides a clear path to accurately converting fractions to percentages. Remember to consider the context and choose an appropriate level of rounding for your calculations. With practice and a solid understanding of the fundamentals, you can confidently tackle various percentage-related problems in diverse fields. The ability to seamlessly translate fractions into percentages is a significant step towards a more thorough grasp of mathematical concepts and their practical applications.
Latest Posts
Latest Posts
-
30 Days From April 16
Sep 14, 2025
-
How Long Until 12 30
Sep 14, 2025
-
9 Inch Diameter Circle Area
Sep 14, 2025
-
58 Sq Meters In Feet
Sep 14, 2025
-
Inverse Of A Matrix Calculator
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 5 7 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.