5 More Than -2 Is
wordexpert
Sep 22, 2025 · 6 min read
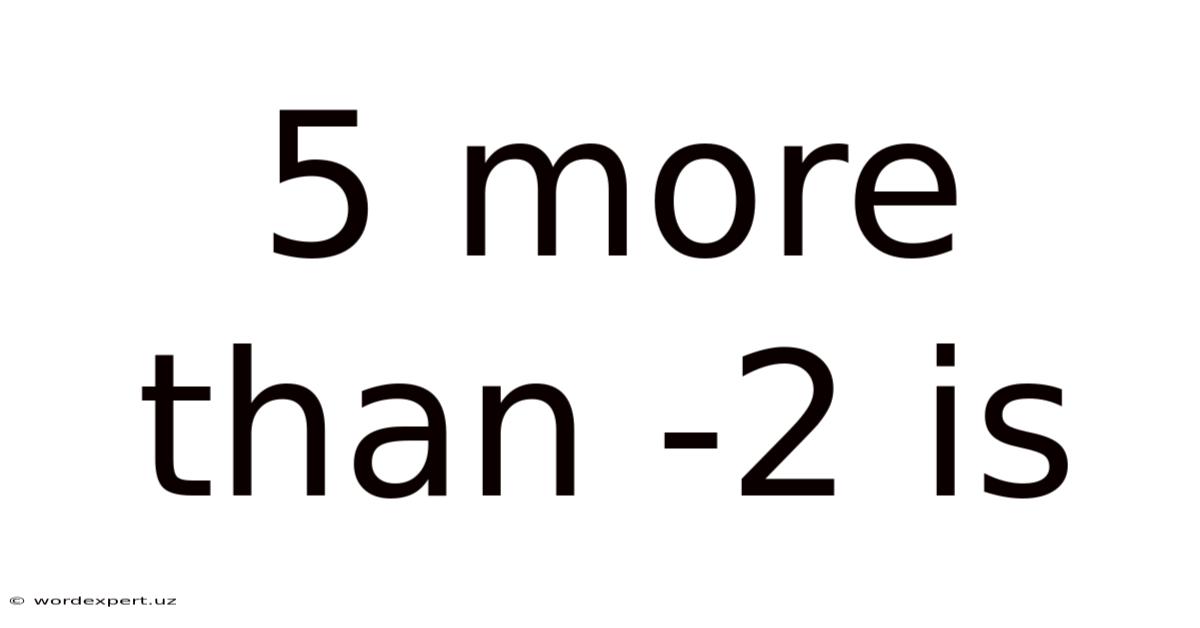
Table of Contents
5 More Than -2 Is: Exploring Integer Addition and its Applications
This article explores the seemingly simple mathematical question: "5 more than -2 is?" While the answer might appear immediately obvious to some, a deeper dive reveals fundamental concepts in integer arithmetic, its practical applications, and the importance of conceptual understanding in mathematics. We'll not only solve this problem but also unpack the underlying principles to build a strong foundation in number operations. This is crucial for anyone learning basic arithmetic, preparing for standardized tests, or simply seeking to improve their mathematical reasoning skills.
Understanding Integers and the Number Line
Before we tackle the problem, let's establish a firm grasp of integers. Integers are whole numbers, including zero, and their negative counterparts. They can be represented on a number line, a visual tool that helps illustrate their relationships:
... -3 -2 -1 0 1 2 3 ...
The number line extends infinitely in both positive and negative directions. Zero sits at the center, separating positive integers (to the right) from negative integers (to the left). Understanding the number line is key to comprehending integer addition and subtraction.
Visualizing "5 More Than -2"
The phrase "5 more than -2" implies addition. We are asked to find the result of adding 5 to -2. We can visualize this on the number line:
- Start at -2.
- Move 5 units to the right (since we're adding a positive number).
Each step to the right represents adding 1. After 5 steps, we land on 3. Therefore, 5 more than -2 is 3.
The Mathematical Operation: Addition of Integers
Mathematically, we represent this as:
-2 + 5 = 3
This is a simple addition problem involving integers. The key to understanding integer addition is to consider the signs of the numbers:
- Adding a positive number: Moves to the right on the number line.
- Adding a negative number: Moves to the left on the number line.
Let's explore some other examples to solidify this understanding:
- -7 + 3 = -4: Start at -7, move 3 units to the right.
- 4 + (-6) = -2: Start at 4, move 6 units to the left.
- -5 + (-2) = -7: Start at -5, move 2 units to the left.
These examples showcase the mechanics of integer addition. The sign of the result depends on the magnitude (absolute value) and signs of the numbers being added. If the positive number has a larger magnitude, the result is positive. If the negative number has a larger magnitude, the result is negative.
Beyond the Number Line: The Absolute Value Concept
While the number line provides a helpful visual, understanding absolute value enhances our ability to work with integers. The absolute value of a number is its distance from zero, regardless of its sign. It is always non-negative. We denote absolute value using vertical bars: |x|.
For example:
- |3| = 3
- |-3| = 3
- |0| = 0
Absolute value helps simplify integer addition, particularly when dealing with numbers of varying signs. Consider the problem -2 + 5. We can think of it as the difference between the absolute values, with the sign determined by the number with the larger absolute value:
|5| - |-2| = 5 - 2 = 3
Since 5 (the positive number) has a larger absolute value, the result is positive 3.
Real-World Applications of Integer Addition
The seemingly simple concept of adding integers finds numerous real-world applications:
-
Finance: Tracking income and expenses. A positive number represents income, while a negative number represents expenses. Calculating net income involves adding these values. For instance, if you earn $50 and spend $20, your net income is $50 + (-$20) = $30.
-
Temperature: Measuring temperature changes. A rise in temperature is represented by a positive number, while a drop in temperature is represented by a negative number. If the temperature was -2°C and increased by 5°C, the new temperature is -2°C + 5°C = 3°C.
-
Altitude: Tracking changes in elevation. Positive numbers represent height above sea level, while negative numbers represent depth below sea level. If a submarine starts at -200 meters and ascends 50 meters, its new depth is -200 meters + 50 meters = -150 meters.
-
Accounting: Calculating profit and loss. Profit is represented by a positive number, and loss is represented by a negative number.
-
Game Scoring: In many games, points can be gained (positive) or lost (negative). Calculating a player's final score involves integer addition.
These are just a few examples of how integer addition plays a vital role in our daily lives and various fields.
Expanding the Concept: Addition with More Than Two Integers
The principles discussed so far extend to adding more than two integers. We can add multiple integers by following the same rules: moving right for positive numbers and left for negative numbers on the number line or considering the absolute values and signs.
Example: -3 + 7 + (-2) + 4
-
Visual Approach (Number Line): Start at -3, move 7 units right (to 4), then 2 units left (to 2), and finally 4 units right (to 6). The answer is 6.
-
Absolute Value Approach: Group the positive and negative numbers separately:
Positive numbers: 7 + 4 = 11 Negative numbers: -3 + (-2) = -5
Add the sums: 11 + (-5) = 6
Both methods lead to the same correct answer.
Frequently Asked Questions (FAQ)
-
Q: What happens if I add a positive and a negative number with the same absolute value?
A: The result is zero. For example, 5 + (-5) = 0. This is because the movements on the number line cancel each other out.
-
Q: Can I add integers in any order?
A: Yes, integer addition is commutative, meaning the order of the numbers does not affect the result. For example, -2 + 5 is the same as 5 + (-2). This property simplifies calculations.
-
Q: What if I have a long string of integers to add?
A: You can group the positive and negative integers separately, add each group, and then add the results. Alternatively, you can use a calculator or computer software to perform the addition.
-
Q: How do I subtract integers?
A: Subtracting an integer is the same as adding its opposite. For example, subtracting 5 is the same as adding -5. So, 3 - 5 is the same as 3 + (-5) = -2.
Conclusion: Mastering Integer Addition
Understanding the concept of "5 more than -2 is" involves more than just getting the correct answer (3). It's about grasping the fundamental principles of integer addition, visualizing it on the number line, using absolute value for simplification, and recognizing its wide range of applications in the real world. By mastering these principles, you develop a strong foundation in arithmetic, enhancing your problem-solving skills and opening doors to more advanced mathematical concepts. The seemingly simple act of adding integers is a building block for more complex mathematical operations and a crucial skill for success in various academic and professional pursuits. Practice regularly and use different methods to solidify your understanding, transforming this seemingly simple concept into a powerful tool in your mathematical arsenal.
Latest Posts
Latest Posts
-
What Is 1 Of 50
Sep 23, 2025
-
Calculo De Salario El Salvador
Sep 23, 2025
-
Standard Height Of A Table
Sep 23, 2025
-
Is 100 Lakhs 1 Crore
Sep 23, 2025
-
90 Days From April 9
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 5 More Than -2 Is . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.