5 Percent Of 1 Million
wordexpert
Sep 19, 2025 · 5 min read
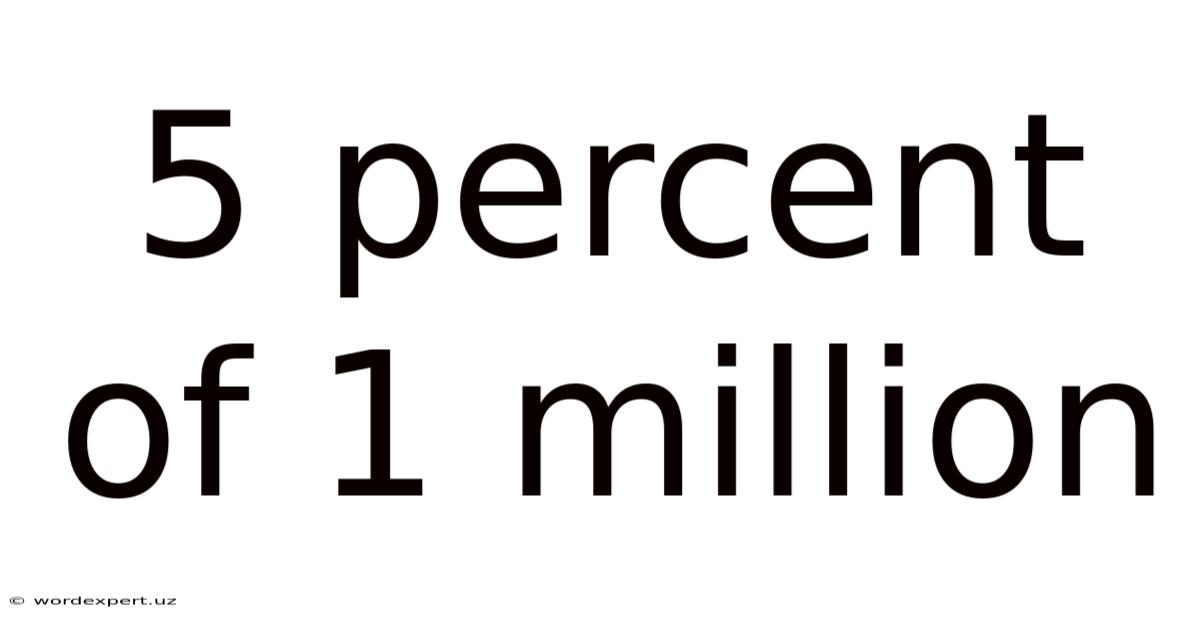
Table of Contents
Decoding 5 Percent of 1 Million: A Comprehensive Guide
Finding 5 percent of 1 million might seem like a simple arithmetic problem, suitable only for elementary school students. However, understanding this calculation extends far beyond basic math. It's a fundamental concept with wide-ranging applications in finance, business, statistics, and everyday life. This comprehensive guide will not only show you how to calculate 5% of 1 million but also explore the practical implications and delve into related percentage calculations. We'll demystify the process, making it accessible to everyone regardless of their mathematical background.
Calculating 5% of 1 Million: The Basic Approach
The most straightforward way to calculate 5% of 1 million is to convert the percentage to a decimal and then multiply. Remember that a percentage is simply a fraction out of 100. Therefore, 5% can be written as 5/100 or 0.05.
Here's the calculation:
0.05 * 1,000,000 = 50,000
Therefore, 5% of 1 million is 50,000.
Alternative Methods: Different Perspectives on Percentage Calculation
While the above method is the most efficient, let's explore other approaches to solidify your understanding and illustrate the flexibility of percentage calculations.
- Using Fractions: We can express 5% as the fraction 5/100. Simplifying this fraction gives us 1/20. Therefore, finding 5% of 1 million is equivalent to finding 1/20 of 1 million:
1,000,000 / 20 = 50,000
This method highlights the relationship between percentages and fractions.
- Breaking Down the Percentage: We can also break down the calculation into smaller, more manageable steps. For instance, we can find 1% of 1 million first and then multiply by 5:
1% of 1,000,000 = 1,000,000 / 100 = 10,000 5% of 1,000,000 = 10,000 * 5 = 50,000
This approach is particularly useful when dealing with more complex percentage calculations or when working with a calculator that doesn't have a percentage function.
- Using Proportions: We can set up a proportion to solve for the unknown value (x):
5/100 = x/1,000,000
Cross-multiplying and solving for x:
100x = 5,000,000 x = 50,000
Real-World Applications: Where This Calculation Matters
Understanding how to calculate 5% of 1 million has practical implications across various fields:
-
Finance: Calculating interest on large sums of money, determining commission on sales, understanding tax implications, and evaluating investment returns all involve percentage calculations. For example, a 5% interest rate on a $1 million investment would yield $50,000 in interest annually.
-
Business: Businesses use percentage calculations extensively in budgeting, pricing strategies, profit margin analysis, and sales forecasting. A 5% discount on a $1 million product would be a $50,000 reduction.
-
Statistics: Percentages are fundamental to descriptive statistics, allowing us to express data proportions and trends. For example, if a survey of 1 million people showed 5% supported a particular candidate, that represents 50,000 people.
-
Everyday Life: We use percentages daily, from calculating tips in restaurants (e.g., a 15% tip on a $50 bill) to understanding discounts in stores (e.g., a 20% off sale) to interpreting data in news reports (e.g., unemployment rates, inflation rates).
Expanding the Scope: Calculating Other Percentages of 1 Million
The ability to calculate 5% of 1 million can be easily extended to calculate other percentages. The core principle remains the same: convert the percentage to a decimal and multiply.
Let's illustrate with a few examples:
- 10% of 1 million: 0.10 * 1,000,000 = 100,000
- 25% of 1 million: 0.25 * 1,000,000 = 250,000
- 75% of 1 million: 0.75 * 1,000,000 = 750,000
- 1% of 1 million: 0.01 * 1,000,000 = 10,000
Understanding Percentage Increase and Decrease
Percentage calculations aren't limited to finding a percentage of a number. We often need to determine the percentage increase or decrease between two numbers. Let's illustrate with examples relevant to our initial problem.
Percentage Increase: Suppose an initial investment of $1 million increased by 5%. The increase would be $50,000 (as calculated earlier), and the new value would be $1,050,000.
Percentage Decrease: If the $1 million investment decreased by 5%, the decrease would be $50,000, and the new value would be $950,000.
Calculating percentage changes requires understanding the formula:
[(New Value - Old Value) / Old Value] * 100%
Beyond the Basics: Advanced Percentage Calculations
While calculating 5% of 1 million is relatively straightforward, dealing with more complex scenarios requires a deeper understanding of percentage concepts.
-
Compound Interest: Compound interest calculations involve repeatedly applying interest to the principal amount plus accumulated interest. This leads to exponential growth, significantly different from simple interest calculations.
-
Percentage Points vs. Percentage Change: It’s crucial to differentiate between percentage points and percentage change. For example, an increase from 5% to 10% is a 5 percentage point increase, but a 100% percentage increase (because 5 increased by 100% to become 10).
-
Percentage of a Percentage: Calculating a percentage of a percentage involves multiplying the decimal equivalents of the percentages. For example, finding 10% of 5% of 1 million would be: 0.10 * 0.05 * 1,000,000 = 5,000.
Frequently Asked Questions (FAQ)
Q: How can I calculate percentages quickly without a calculator?
A: For simple percentages, mental math techniques can be effective. For example, 10% is easy to calculate by moving the decimal point one place to the left. Other percentages can be broken down into simpler fractions or percentages.
Q: What are some common mistakes people make when calculating percentages?
A: Common errors include incorrect decimal conversion, misinterpreting percentage increase/decrease, and confusing percentage points with percentage change. Carefully review the calculation steps and double-check your work.
Q: Are there any online tools or calculators for percentage calculations?
A: Yes, numerous online calculators are available that can perform complex percentage calculations quickly and accurately.
Q: How does understanding percentages help in financial planning?
A: Understanding percentages is essential for budgeting, tracking expenses, evaluating investment returns, and making informed financial decisions.
Conclusion: Mastering the Power of Percentage Calculations
This comprehensive guide has explored the seemingly simple yet incredibly versatile calculation of 5% of 1 million. We've gone beyond the basic arithmetic to explore various approaches, highlight real-world applications, and delve into more advanced percentage concepts. Mastering percentage calculations is a crucial skill with broad applications, not just in finance and business, but in many areas of life. The ability to understand and utilize percentages empowers you to interpret data, make informed decisions, and navigate the numerical world with confidence. Remember, the foundation lies in understanding the core concept: a percentage is simply a fraction out of 100. From there, you can tackle any percentage calculation with clarity and precision.
Latest Posts
Latest Posts
-
2s Complement To Decimal Calculator
Sep 19, 2025
-
How Long Is 24 Weeks
Sep 19, 2025
-
Cuillere A Soupe En Gr
Sep 19, 2025
-
Cms A Pies Y Pulgadas
Sep 19, 2025
-
How Much Time Until 2 45
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 5 Percent Of 1 Million . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.