5 Percent Of 20 000
wordexpert
Sep 12, 2025 · 5 min read
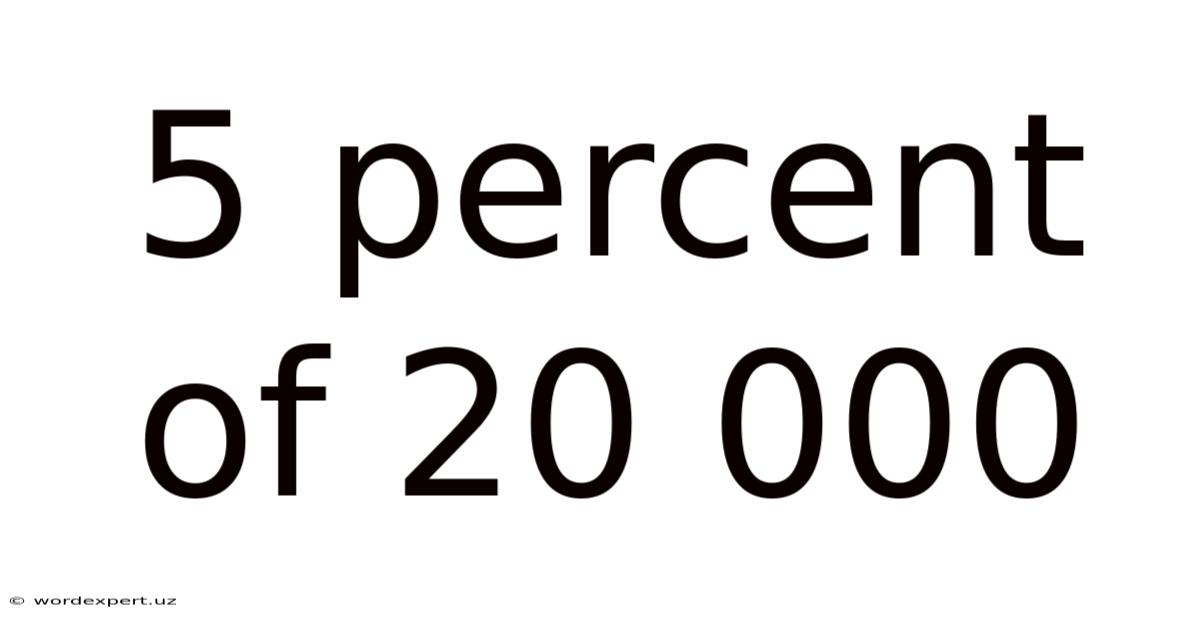
Table of Contents
Decoding 5 Percent of 20,000: A Deep Dive into Percentages and Their Applications
Finding 5 percent of 20,000 might seem like a simple arithmetic problem, suitable only for elementary school. However, understanding how to calculate percentages and their applications extends far beyond basic math. This seemingly straightforward calculation underpins a vast range of applications in finance, statistics, everyday life, and even advanced scientific fields. This article will not only show you how to calculate 5% of 20,000 but will also delve into the underlying concepts, explore different calculation methods, and showcase its relevance in various real-world scenarios.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The term "percent" comes from the Latin "per centum," meaning "out of a hundred." So, 5% means 5 out of every 100. This fundamental understanding allows us to translate percentages into decimals and fractions, providing multiple avenues for calculation.
To express a percentage as a decimal, we divide the percentage by 100. For example, 5% becomes 0.05 (5 ÷ 100 = 0.05). Conversely, to express a decimal as a percentage, we multiply it by 100.
To express a percentage as a fraction, we write the percentage as the numerator and 100 as the denominator. Thus, 5% can be written as 5/100, which simplifies to 1/20.
Calculating 5 Percent of 20,000: Three Approaches
Now, let's tackle the core problem: calculating 5% of 20,000. We can use three different, yet equally valid methods:
1. The Decimal Method:
This is arguably the most straightforward method. We convert the percentage to its decimal equivalent (0.05) and then multiply it by the total value (20,000).
- 5% of 20,000 = 0.05 * 20,000 = 1000
2. The Fraction Method:
This method involves converting the percentage to a fraction and then performing the multiplication.
- 5% = 5/100 = 1/20
- 1/20 * 20,000 = 20,000/20 = 1000
3. The Proportion Method:
This method sets up a proportion to solve for the unknown value.
-
Let 'x' be 5% of 20,000. We can set up the proportion: x/20,000 = 5/100
-
Cross-multiplying, we get: 100x = 100,000
-
Solving for x: x = 100,000/100 = 1000
Real-World Applications: Where Percentages Matter
The seemingly simple calculation of 5% of 20,000 has numerous practical applications across various fields:
-
Finance: Calculating interest earned on savings accounts, determining the discount on sale items, understanding tax rates, and evaluating investment returns all involve percentage calculations. For instance, if you invested $20,000 and earned a 5% return, you would have gained $1,000.
-
Statistics: Percentages are crucial in representing data and drawing conclusions. For instance, if a survey of 20,000 people showed that 5% preferred a particular product, it indicates 1,000 people out of the total sample favored that product. This helps businesses understand market trends and customer preferences. Similarly, understanding percentage change is vital in analyzing economic indicators, population growth, or even the success rate of a medical treatment.
-
Everyday Life: Calculating tips in restaurants, understanding sales tax, figuring out discounts, and even determining the percentage of a certain ingredient in a recipe all involve percentage calculations. For example, a 5% tip on a $20,000 restaurant bill (unlikely, but illustrative) would be $1,000.
-
Science: Percentages are fundamental in various scientific fields. In chemistry, concentration of solutions is often expressed as a percentage. In biology, population growth or decline can be shown as a percentage change. In many experimental setups, percentages are frequently used to express the rate of something, from success rates to error margins.
Beyond the Basics: More Complex Percentage Calculations
While finding 5% of 20,000 is relatively straightforward, more complex scenarios require a deeper understanding of percentage concepts. These include:
-
Finding the Percentage: Instead of finding the percentage of a number, you may need to find what percentage one number represents of another. For instance, if 1000 people out of 20,000 voted for a candidate, what percentage of the total votes did they represent? (Answer: 5%)
-
Finding the Original Amount: You may know the percentage and the resulting amount, but need to find the original amount. For example, if you received a 5% discount and paid $19,000, what was the original price? (This requires solving an equation: 0.95x = 19,000, where x is the original price.)
-
Percentage Increase or Decrease: This involves calculating the percentage change between two values. For example, if a population grew from 10,000 to 10,500, what was the percentage increase? (Answer: 5%)
Percentage Points vs. Percentage Change: A Crucial Distinction
It's important to differentiate between percentage points and percentage change. A percentage point represents an absolute change in percentage, while percentage change represents the relative change from an initial value.
For example:
-
Scenario 1: If interest rates increase from 2% to 7%, the increase is 5 percentage points (7% - 2% = 5%).
-
Scenario 2: If interest rates increase from 2% to 7%, the percentage change is 250% ( (7-2)/2 * 100%).
Frequently Asked Questions (FAQs)
Q1: How do I calculate a percentage on a calculator?
Most calculators have a percentage key (%). To calculate 5% of 20,000, you would enter 20000 x 5 %.
Q2: Are there any online percentage calculators?
Yes, numerous websites offer free online percentage calculators that can perform various percentage-related calculations.
Q3: What if I need to calculate a more complex percentage problem?
For more complex problems, you might need to use algebraic equations or consult a more advanced mathematical resource.
Q4: Can I use spreadsheets (like Excel or Google Sheets) to calculate percentages?
Absolutely! Spreadsheets are powerful tools for performing percentage calculations, especially when working with large datasets.
Conclusion: Mastering Percentages – A Lifelong Skill
Understanding how to calculate percentages, such as finding 5% of 20,000, is more than just a mathematical skill; it's a practical tool applicable in various aspects of life. From personal finance to professional endeavors, mastering percentages empowers you to make informed decisions, analyze data effectively, and navigate complex situations with confidence. While the core concept is relatively simple, the ability to apply this knowledge creatively unlocks a deeper understanding of numerical data and its implications in the world around us. Remember the different methods – decimal, fraction, and proportion – and choose the one that best suits your needs and understanding. The key is not just to get the answer (1000 in this case), but to grasp the underlying principles that enable you to solve a wide array of similar problems.
Latest Posts
Latest Posts
-
2 Grams Yeast To Tsp
Sep 12, 2025
-
How Much Is 1000 Ms
Sep 12, 2025
-
1 Mega Pascal To Psi
Sep 12, 2025
-
Least To Greatest Calculator Decimals
Sep 12, 2025
-
375 Grams To Cups Water
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 5 Percent Of 20 000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.