7 20 As A Percent
wordexpert
Sep 11, 2025 · 6 min read
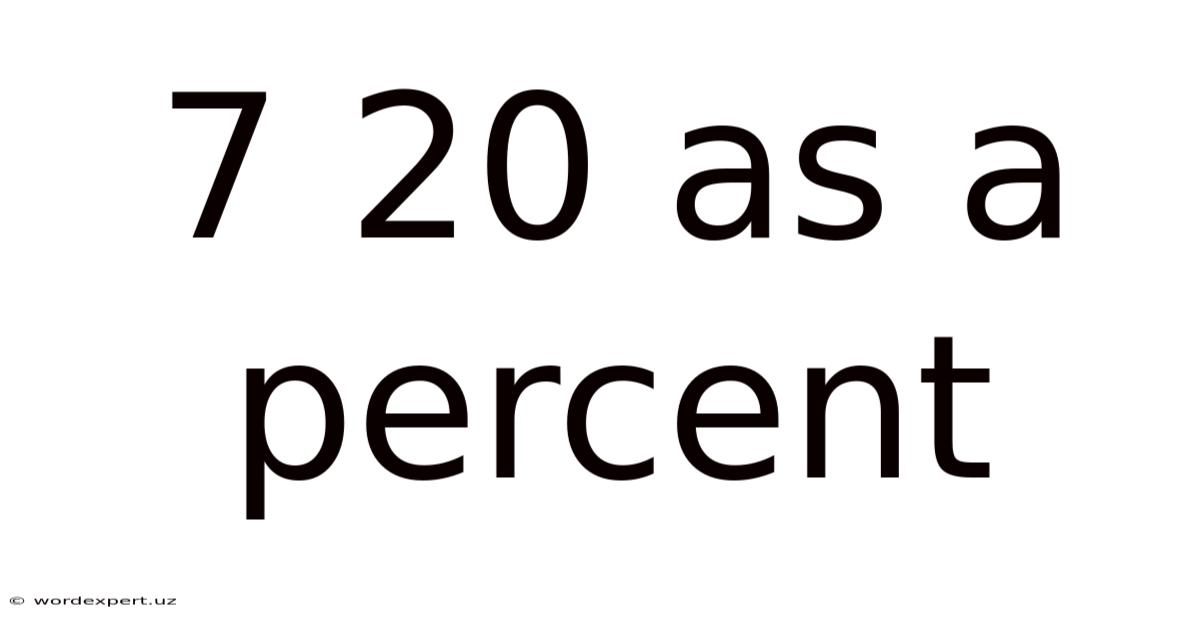
Table of Contents
7/20 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced statistical analysis. This comprehensive guide will walk you through the process of converting the fraction 7/20 into a percentage, explaining the underlying concepts and providing practical examples to solidify your understanding. We'll also explore different methods and address frequently asked questions. By the end, you'll not only know that 7/20 equals 35%, but also understand the why behind the calculation.
Introduction: Understanding Fractions and Percentages
Before we dive into converting 7/20, let's quickly refresh our understanding of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). For example, in the fraction 7/20, 7 is the numerator and 20 is the denominator. This means we're considering 7 parts out of a total of 20 equal parts.
A percentage, on the other hand, expresses a fraction as a number out of 100. The symbol "%" signifies "percent," which literally means "per hundred." So, 35% means 35 out of 100, or 35/100. Converting fractions to percentages involves finding the equivalent fraction with a denominator of 100.
Method 1: The Direct Conversion Method
The most straightforward method to convert 7/20 to a percentage involves setting up a proportion. We want to find a percentage, which means finding an equivalent fraction with a denominator of 100. We can set up the proportion as follows:
7/20 = x/100
To solve for 'x' (the percentage), we cross-multiply:
20x = 700
Now, divide both sides by 20:
x = 700/20 = 35
Therefore, 7/20 is equal to 35%.
Method 2: The Decimal Conversion Method
This method involves two steps: first, converting the fraction to a decimal, and then converting the decimal to a percentage.
- Fraction to Decimal: To convert 7/20 to a decimal, we simply divide the numerator (7) by the denominator (20):
7 ÷ 20 = 0.35
- Decimal to Percentage: To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol:
0.35 × 100 = 35%
So, again, we arrive at the answer: 7/20 = 35%.
Method 3: Simplifying the Fraction (Optional)
While not necessary for this particular fraction, simplifying fractions before conversion can sometimes make the calculation easier. However, 7/20 is already in its simplest form because 7 and 20 share no common factors other than 1. If the fraction were, for example, 14/40, we could simplify it by dividing both the numerator and denominator by 2, resulting in 7/20, making the conversion to a percentage simpler.
Visual Representation: Understanding the Concept
Imagine you have a pizza cut into 20 equal slices. If you eat 7 slices, you've eaten 7/20 of the pizza. To express this as a percentage, we're essentially asking: "What percentage of the pizza did you eat?" The answer, as we've calculated, is 35%. This visual representation can help solidify the understanding of the concept.
Real-World Applications of Percentage Conversions
Converting fractions to percentages is a practical skill used in various real-world scenarios:
-
Calculating Discounts: If a store offers a 25% discount on an item, and the original price is represented as a fraction, you would need to convert the fraction to a percentage to calculate the discount amount.
-
Analyzing Data: In statistics and data analysis, percentages are frequently used to represent proportions and probabilities. Converting fractions to percentages allows for easier interpretation and comparison of data.
-
Financial Calculations: Percentages are fundamental in financial calculations, such as interest rates, tax calculations, and profit margins. Understanding fraction-to-percentage conversion is crucial for effective financial management.
-
Academic Assessments: Grades are often expressed as percentages, and converting fractional scores to percentages allows for easier comparison and evaluation of student performance.
Explanation in More Detail: The Mathematics Behind the Conversion
The core of converting a fraction to a percentage lies in the understanding that a percentage is simply a fraction with a denominator of 100. The process we followed – whether using the direct proportion method or the decimal method – is essentially finding an equivalent fraction with a denominator of 100. Multiplying the fraction by 100/100 (which is equal to 1 and therefore doesn't change the value of the fraction) facilitates this conversion.
Let’s break down the proportion method again:
7/20 = x/100
To solve for 'x', we aim to isolate it. We achieve this by multiplying both sides of the equation by 100. This cancels out the 100 on the right side and leaves 'x' by itself. On the left side, you're essentially multiplying the fraction 7/20 by 100. This results in:
x = (7/20) * 100
This simplifies to:
x = 35
This demonstrates the mathematical foundation of the process.
Frequently Asked Questions (FAQ)
-
Q: Can I convert any fraction to a percentage? A: Yes, any fraction can be converted to a percentage. However, some fractions may result in repeating or non-terminating decimals, leading to slightly less precise percentage representations.
-
Q: What if the fraction is a mixed number (e.g., 1 3/4)? A: First, convert the mixed number into an improper fraction (7/4 in this case), then follow the steps outlined above for converting fractions to percentages.
-
Q: Is there a shortcut for converting fractions with denominators that are factors of 100? A: Yes, if the denominator is a factor of 100 (e.g., 2, 4, 5, 10, 20, 25, 50), you can easily find an equivalent fraction with a denominator of 100 by multiplying both the numerator and denominator by the appropriate factor.
-
Q: Why is the percentage always out of 100? A: The term "percent" itself means "out of 100." Percentages provide a standardized way to express proportions, making comparisons easier than using different fractions with varying denominators.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting 7/20 to a percentage, as we've shown, yields 35%. Understanding the methods and the underlying principles of fraction-to-percentage conversion is crucial for success in various mathematical and real-world applications. By mastering this skill, you'll be better equipped to tackle various quantitative problems and analyze data more effectively. Remember that the key is to find an equivalent fraction with a denominator of 100, whether through direct proportion, decimal conversion, or simplification. Practice makes perfect, so try converting different fractions to percentages to reinforce your understanding and build confidence in your skills.
Latest Posts
Latest Posts
-
Inch Of Water To Psi
Sep 11, 2025
-
Degree Angle To Percent Slope
Sep 11, 2025
-
Born In 1994 How Old
Sep 11, 2025
-
Square Yard To Cubic Yard
Sep 11, 2025
-
77 Weeks Ago From Today
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 7 20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.