7 25 As A Percent
wordexpert
Sep 24, 2025 · 5 min read
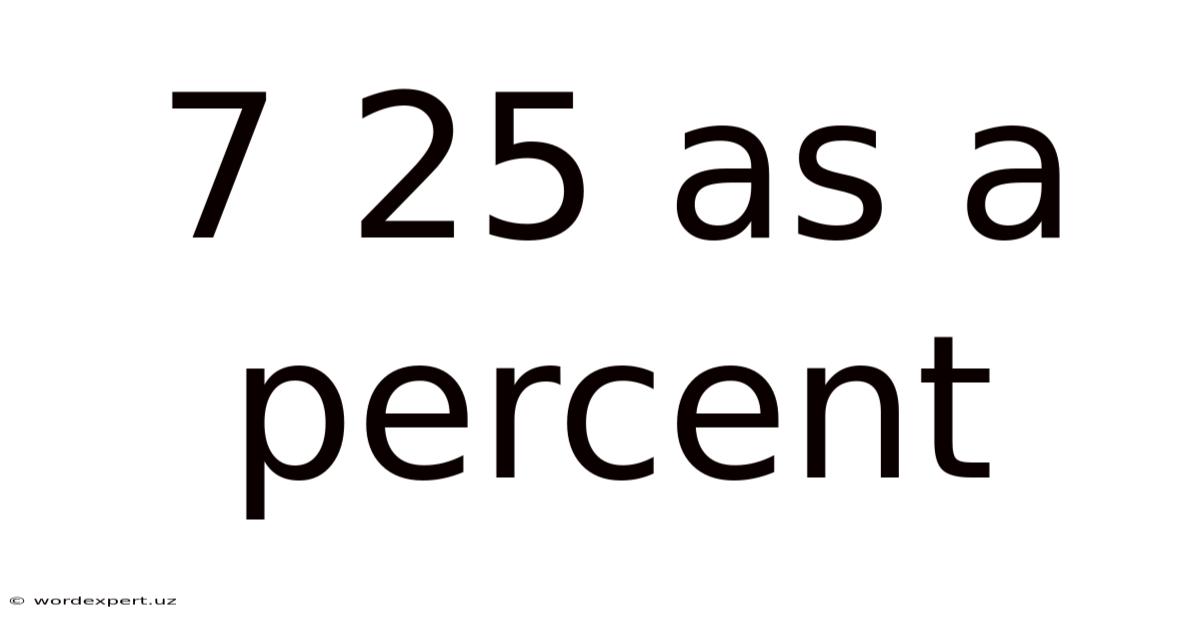
Table of Contents
7/25 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with widespread applications in everyday life, from calculating discounts and tips to understanding statistics and financial data. This comprehensive guide will walk you through the process of converting the fraction 7/25 into a percentage, explaining the underlying principles and providing practical examples to solidify your understanding. We'll also explore different methods and address common questions to ensure you feel confident in tackling similar conversions in the future.
Introduction: Understanding Fractions and Percentages
Before diving into the conversion of 7/25, let's briefly review the concepts of fractions and percentages. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of parts the whole is divided into.
A percentage, on the other hand, represents a fraction out of 100. The term "percent" literally means "per hundred." Therefore, a percentage expresses a proportion as a fraction with a denominator of 100. For example, 50% means 50 out of 100, which can be written as the fraction 50/100 or the decimal 0.5.
Method 1: Converting the Fraction to a Decimal then to a Percentage
This is arguably the most straightforward method. We begin by converting the fraction 7/25 into a decimal. To do this, we simply divide the numerator (7) by the denominator (25):
7 ÷ 25 = 0.28
Now that we have the decimal equivalent (0.28), converting it to a percentage is a simple matter of multiplying by 100 and adding the "%" symbol:
0.28 × 100 = 28%
Therefore, 7/25 is equal to 28%.
Method 2: Finding an Equivalent Fraction with a Denominator of 100
Another way to convert 7/25 to a percentage is to find an equivalent fraction with a denominator of 100. This involves finding a number that, when multiplied by the original denominator (25), results in 100. In this case, that number is 4 (because 25 x 4 = 100).
To maintain the equivalence of the fraction, we must multiply both the numerator and the denominator by the same number:
(7 × 4) / (25 × 4) = 28/100
Since a percentage is a fraction out of 100, we can directly express 28/100 as a percentage: 28%.
Method 3: Using Proportions
A more formal approach involves setting up a proportion. We know that 7/25 represents a certain percentage, let's call it 'x'. We can set up the following proportion:
7/25 = x/100
To solve for 'x', we can cross-multiply:
7 × 100 = 25 × x
700 = 25x
Now, divide both sides by 25:
x = 700 ÷ 25 = 28
Therefore, x = 28, meaning 7/25 is equivalent to 28%.
The Significance of Understanding Fraction-to-Percentage Conversions
The ability to convert fractions to percentages isn't just an academic exercise; it's a crucial skill with practical applications in numerous fields. Consider these examples:
- Financial Calculations: Calculating interest rates, discounts, tax rates, and profit margins often involves converting fractions to percentages. For instance, a 1/4 discount on an item translates to a 25% discount.
- Data Analysis and Statistics: Percentages are commonly used to represent proportions in data sets. Converting fractions allows for easier comparison and interpretation of statistical information.
- Everyday Life: Understanding percentages aids in making informed decisions in daily life, such as comparing prices, understanding sales, and calculating tips.
Beyond 7/25: Applying the Methods to Other Fractions
The methods described above for converting 7/25 to a percentage are applicable to any fraction. Let's illustrate with a few more examples:
-
Converting 3/4 to a percentage:
- Method 1 (Decimal to Percentage): 3 ÷ 4 = 0.75; 0.75 × 100 = 75%
- Method 2 (Equivalent Fraction): (3 × 25) / (4 × 25) = 75/100 = 75%
- Method 3 (Proportion): 3/4 = x/100; 300 = 4x; x = 75%
-
Converting 1/8 to a percentage:
- Method 1 (Decimal to Percentage): 1 ÷ 8 = 0.125; 0.125 × 100 = 12.5%
- Method 2 (Equivalent Fraction): (1 × 12.5) / (8 × 12.5) = 12.5/100 = 12.5%
- Method 3 (Proportion): 1/8 = x/100; 100 = 8x; x = 12.5%
Frequently Asked Questions (FAQ)
-
Q: What if the fraction is an improper fraction (where the numerator is larger than the denominator)?
A: You can still use the same methods. The resulting percentage will be greater than 100%. For example, converting 5/2 to a percentage: 5 ÷ 2 = 2.5; 2.5 × 100 = 250%.
-
Q: Can I use a calculator to convert fractions to percentages?
A: Yes, most calculators have the capability to perform these conversions directly. Simply divide the numerator by the denominator, then multiply the result by 100.
-
Q: Why is understanding percentages important?
A: Percentages provide a standardized way to compare and interpret proportions. They are essential for various real-world applications, from financial calculations to understanding data analysis.
Conclusion: Mastering Percentage Conversions
Converting fractions to percentages is a vital mathematical skill with numerous practical applications. This guide has explored three different methods for converting 7/25 to a percentage – all leading to the same answer: 28%. Understanding these methods, along with the underlying concepts of fractions and percentages, empowers you to confidently tackle similar conversions and apply this knowledge to various real-world scenarios. Remember to practice regularly to reinforce your understanding and build fluency in this essential mathematical skill. The more you practice, the more intuitive and effortless this process will become. Don't hesitate to revisit these methods and examples as needed, and soon you'll be converting fractions to percentages with ease and confidence.
Latest Posts
Latest Posts
-
How Long Until 2 18
Sep 24, 2025
-
90 Days From March 30
Sep 24, 2025
-
60 Days From August 7
Sep 24, 2025
-
Formula For Right Triangle Perimeter
Sep 24, 2025
-
How Long Is 80 Minutes
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 7 25 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.