7 Out Of 11 Percentage
wordexpert
Sep 19, 2025 · 5 min read
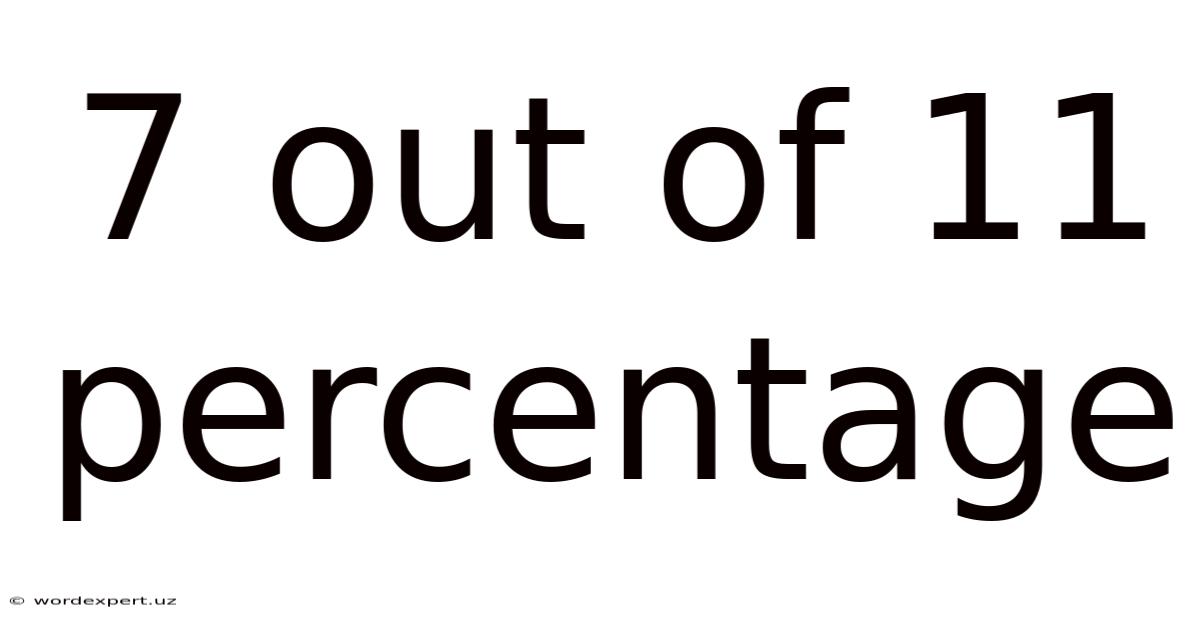
Table of Contents
Decoding 7 out of 11: Understanding Percentages, Ratios, and Proportions
Understanding percentages is a fundamental skill in everyday life, from calculating discounts and tax to analyzing data and interpreting statistics. This article will delve deep into the meaning of "7 out of 11," exploring its representation as a percentage, ratio, and proportion, and showing how to apply these concepts in various scenarios. We'll also look at practical applications and address frequently asked questions, ensuring a comprehensive understanding of this seemingly simple yet powerful mathematical concept.
What does 7 out of 11 mean?
The phrase "7 out of 11" represents a fraction where 7 is the numerator (the part) and 11 is the denominator (the whole). It signifies that out of a total of 11 items or events, 7 possess a specific characteristic or outcome. This fraction can be expressed in several ways, each providing a different perspective on the data.
Calculating the Percentage: From Fraction to Percentage
Converting the fraction 7/11 into a percentage involves multiplying the fraction by 100%. This process essentially scales the fraction to represent a portion of 100, making comparisons and interpretations easier.
Here's the calculation:
(7/11) * 100% ≈ 63.64%
Therefore, 7 out of 11 represents approximately 63.64%. The "~" symbol indicates that this is an approximation due to rounding. The percentage shows that approximately 63.64 out of every 100 items or events would share the same characteristic.
Understanding Ratios: Expressing Relationships
A ratio expresses the quantitative relationship between two or more amounts. In the case of "7 out of 11," the ratio is 7:11 (read as "7 to 11"). This indicates the relative proportion of the part (7) to the whole (11). Ratios are useful for comparing quantities directly, without necessarily expressing them as a percentage. For example, you might say "the ratio of successful attempts to total attempts is 7:11."
Exploring Proportions: Scaling the Relationship
A proportion is a statement that two ratios are equal. Proportions are invaluable for solving problems where we know a part and the whole, and want to find a corresponding part in a larger or smaller whole. For instance, if we know that 7 out of 11 students passed an exam, and we have a total of 33 students, we can use a proportion to find how many students passed in the larger group:
7/11 = x/33
To solve for 'x' (the number of students who passed in the larger group), we cross-multiply:
11x = 7 * 33 11x = 231 x = 21
Therefore, 21 out of 33 students passed the exam. This demonstrates the power of proportions in scaling up or down the original relationship between 7 and 11.
Practical Applications of 7 out of 11
The concept of "7 out of 11" and its equivalent percentage (approximately 63.64%) has numerous real-world applications:
-
Sports Statistics: Imagine a basketball player who made 7 out of 11 free throws. Their free-throw percentage is approximately 63.64%. This statistic is a crucial performance indicator.
-
Quality Control: In a manufacturing setting, if 7 out of 11 products pass inspection, the pass rate is approximately 63.64%. This informs decisions about production processes and quality improvements.
-
Surveys and Polls: If 7 out of 11 respondents to a survey favored a particular candidate, the candidate's support is around 63.64%. This is a vital data point for political strategists and pollsters.
-
Medical Trials: In a clinical trial, if 7 out of 11 participants responded positively to a new treatment, the success rate is approximately 63.64%. This data informs the effectiveness and safety of the treatment.
-
Academic Performance: If a student answered 7 out of 11 questions correctly on a test, their score is approximately 63.64%. This reflects their understanding of the subject matter.
Beyond the Numbers: Interpreting the Results
While the numerical calculations are important, the interpretation of the results is equally crucial. A 63.64% success rate could be considered high, low, or average, depending on the context. Factors to consider include:
-
Benchmarking: How does this rate compare to previous results, industry standards, or expectations? A 63.64% success rate might be excellent in one context but poor in another.
-
Margin of Error: Statistical data often includes a margin of error. Understanding the margin of error is critical in accurately interpreting the significance of the 63.64% figure.
-
Underlying Factors: Are there other factors that might explain the 7 out of 11 result? This requires a deeper investigation beyond the simple numerical representation.
Advanced Concepts: Probability and Statistics
The concepts related to 7 out of 11 extend into the realms of probability and statistics. The fraction 7/11 can be interpreted as the probability of a successful outcome in a specific event. Statistical analyses can help to determine whether the observed result (7 out of 11) is statistically significant or simply due to random chance. This involves concepts like hypothesis testing, confidence intervals, and statistical significance.
Frequently Asked Questions (FAQ)
Q: How do I convert a percentage to a fraction?
A: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 60% becomes 60/100, which simplifies to 3/5.
Q: How do I convert a decimal to a percentage?
A: To convert a decimal to a percentage, multiply the decimal by 100 and add a "%" symbol. For example, 0.75 becomes 0.75 * 100% = 75%.
Q: What if I have more than two quantities to compare?
A: When comparing more than two quantities, you can use extended ratios. For example, if you have 3 quantities in the ratio 2:3:5, this means that for every 2 units of the first quantity, there are 3 units of the second and 5 units of the third.
Q: How can I improve my understanding of percentages and ratios?
A: Practice is key. Work through various problems, from simple calculations to more complex applications. Utilize online resources, textbooks, and educational videos to reinforce your understanding.
Conclusion: Mastering the Fundamentals
Understanding "7 out of 11," whether expressed as a fraction, percentage, ratio, or incorporated into a proportion, provides a foundation for tackling more complex mathematical concepts. The ability to interpret and apply these concepts is invaluable across diverse fields, from everyday finances to advanced scientific research. By mastering these fundamental skills, you'll enhance your problem-solving capabilities and improve your comprehension of quantitative data in all its forms. Remember, the key is not just knowing the calculations, but also understanding the context and interpreting the results meaningfully.
Latest Posts
Latest Posts
-
1 Ml Drops To Syrup
Sep 19, 2025
-
30 Mpg To L 100
Sep 19, 2025
-
Swimming Suit For Body Type
Sep 19, 2025
-
Is 13 16 Bigger Than 3 4
Sep 19, 2025
-
Convert 90 C To F
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 7 Out Of 11 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.