Gcf Of 26 And 39
wordexpert
Sep 16, 2025 · 6 min read
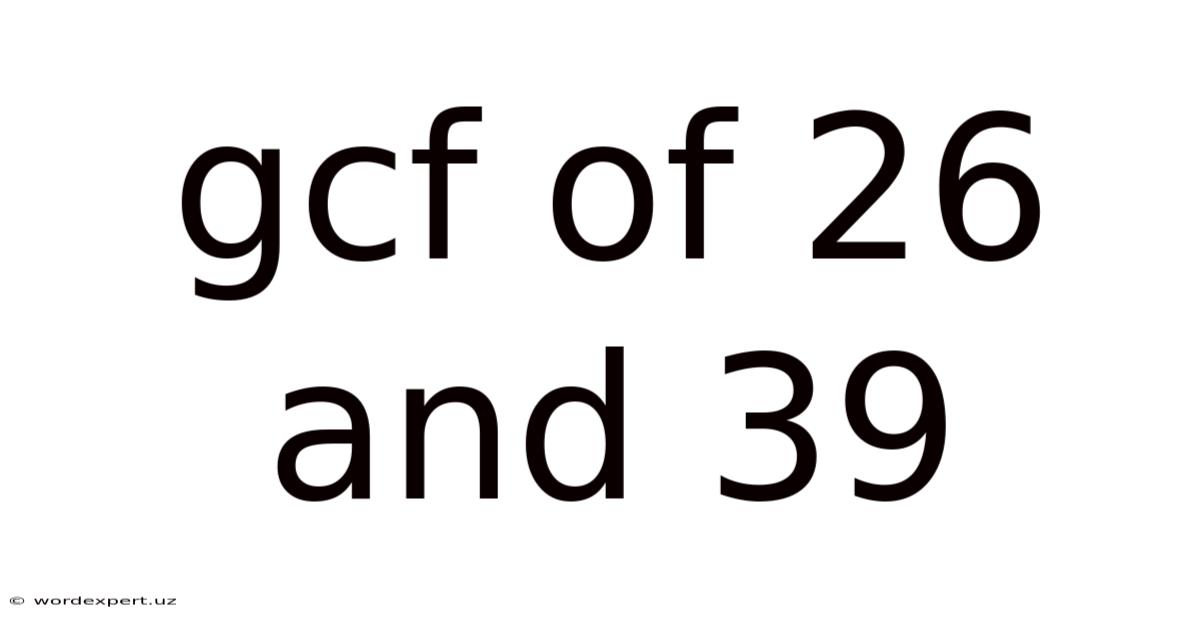
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 26 and 39: A Comprehensive Guide
Finding the Greatest Common Factor (GCF), also known as the Highest Common Factor (HCF) or Greatest Common Divisor (GCD), of two numbers is a fundamental concept in mathematics. This article delves deep into the process of determining the GCF of 26 and 39, exploring various methods and providing a comprehensive understanding of the underlying principles. Understanding GCFs is crucial for simplifying fractions, solving algebraic equations, and tackling more advanced mathematical concepts. We'll cover multiple approaches, ensuring you grasp the concept fully, regardless of your mathematical background.
Understanding Greatest Common Factor (GCF)
Before we tackle the specific case of 26 and 39, let's solidify our understanding of the GCF. The GCF of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that perfectly divides both numbers. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 evenly.
Method 1: Listing Factors
The simplest method to find the GCF is by listing all the factors of each number and identifying the largest common factor.
Factors of 26: 1, 2, 13, 26
Factors of 39: 1, 3, 13, 39
By comparing the two lists, we can see that the common factors are 1 and 13. The greatest of these common factors is 13. Therefore, the GCF of 26 and 39 is 13.
This method works well for smaller numbers, but it becomes less efficient as the numbers get larger and have more factors.
Method 2: Prime Factorization
Prime factorization involves expressing a number as a product of its prime factors. Prime numbers are numbers greater than 1 that are only divisible by 1 and themselves (e.g., 2, 3, 5, 7, 11, etc.). This method is particularly useful for larger numbers.
Let's find the prime factorization of 26 and 39:
- Prime factorization of 26: 26 = 2 × 13
- Prime factorization of 39: 39 = 3 × 13
Once we have the prime factorizations, we identify the common prime factors and multiply them together. Both 26 and 39 share the prime factor 13. Therefore, the GCF of 26 and 39 is 13.
This method is more systematic and efficient than listing factors, especially when dealing with larger numbers. It provides a clearer understanding of the number's composition and helps in identifying the common factors more effectively.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. This algorithm is based on the principle that the GCF of two numbers does not change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, and that number is the GCF.
Let's apply the Euclidean algorithm to find the GCF of 26 and 39:
- Start with the larger number (39) and the smaller number (26).
- Subtract the smaller number from the larger number: 39 - 26 = 13
- Replace the larger number with the result (13) and keep the smaller number (26). Now we have the numbers 13 and 26.
- Repeat the subtraction: 26 - 13 = 13
- Now both numbers are 13. The process stops here.
Therefore, the GCF of 26 and 39 is 13.
The Euclidean algorithm is a powerful tool because it avoids the need for complete prime factorization, making it significantly faster for larger numbers. Its iterative nature guarantees a solution in a finite number of steps.
Illustrative Examples: Extending the Concepts
To solidify your understanding, let's explore a few more examples using the prime factorization method and the Euclidean algorithm.
Example 1: Finding the GCF of 48 and 72
-
Prime Factorization:
- 48 = 2 × 2 × 2 × 2 × 3 = 2<sup>4</sup> × 3
- 72 = 2 × 2 × 2 × 3 × 3 = 2<sup>3</sup> × 3<sup>2</sup>
- Common factors: 2<sup>3</sup> × 3 = 8 × 3 = 24. Therefore, the GCF(48, 72) = 24
-
Euclidean Algorithm:
- 72 - 48 = 24
- 48 - 24 = 24
- GCF(48, 72) = 24
Example 2: Finding the GCF of 105 and 135
-
Prime Factorization:
- 105 = 3 × 5 × 7
- 135 = 3 × 3 × 3 × 5 = 3<sup>3</sup> × 5
- Common factors: 3 × 5 = 15. Therefore, the GCF(105, 135) = 15
-
Euclidean Algorithm:
- 135 - 105 = 30
- 105 - 30 = 75
- 75 - 30 = 45
- 45 - 30 = 15
- 30 - 15 = 15
- GCF(105, 135) = 15
Applications of GCF in Real-World Scenarios
Understanding GCF has practical applications beyond theoretical mathematics. Here are a few examples:
-
Simplifying Fractions: Finding the GCF of the numerator and denominator allows for simplifying fractions to their lowest terms. For instance, the fraction 26/39 can be simplified to 2/3 by dividing both the numerator and denominator by their GCF, which is 13.
-
Dividing Objects Equally: Imagine you have 26 apples and 39 oranges, and you want to divide them into identical groups. The GCF (13) tells you that you can create 13 identical groups, each with 2 apples and 3 oranges.
-
Measurement and Construction: In construction or design, GCF can help determine the largest common unit of measurement for a project, optimizing material usage and ensuring consistency.
-
Data Analysis: In data analysis and computer science, GCF is used in various algorithms related to number theory and cryptography.
Frequently Asked Questions (FAQ)
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, the numbers are called relatively prime or coprime. This means they share no common factors other than 1.
Q: Can the GCF of two numbers be larger than the smaller number?
A: No, the GCF of two numbers can never be larger than the smaller of the two numbers.
Q: Is there a limit to the number of methods to find the GCF?
A: While the methods described here are the most common and efficient, there are other less frequently used methods, depending on the complexity of the numbers involved and the context of the problem.
Q: What if I have more than two numbers? How do I find the GCF?
A: To find the GCF of more than two numbers, you can use any of the methods described above, but you would apply them iteratively. For example, first find the GCF of two numbers, then find the GCF of that result and the next number, and so on.
Conclusion
Finding the Greatest Common Factor is a fundamental skill in mathematics with wide-ranging applications. We've explored three efficient methods – listing factors, prime factorization, and the Euclidean algorithm – to determine the GCF, providing practical examples and tackling frequently asked questions. Mastering these techniques equips you with a powerful toolset for solving various mathematical problems and understanding the underlying principles of number theory. Regardless of whether you use prime factorization, the Euclidean algorithm, or the simpler method of listing factors, the GCF of 26 and 39 remains consistently 13. Understanding the different approaches allows you to choose the most efficient method depending on the numbers you are working with. Remember, practice is key to mastering these concepts and applying them effectively.
Latest Posts
Latest Posts
-
200 Dias Sao Quantos Meses
Sep 16, 2025
-
45 000 Dollars In Rupees
Sep 16, 2025
-
96 Weeks Ago From Today
Sep 16, 2025
-
Guinea Pig To Human Years
Sep 16, 2025
-
Volusia County Florida Sales Tax
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 26 And 39 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.