Gcf Of 36 And 81
wordexpert
Sep 23, 2025 · 6 min read
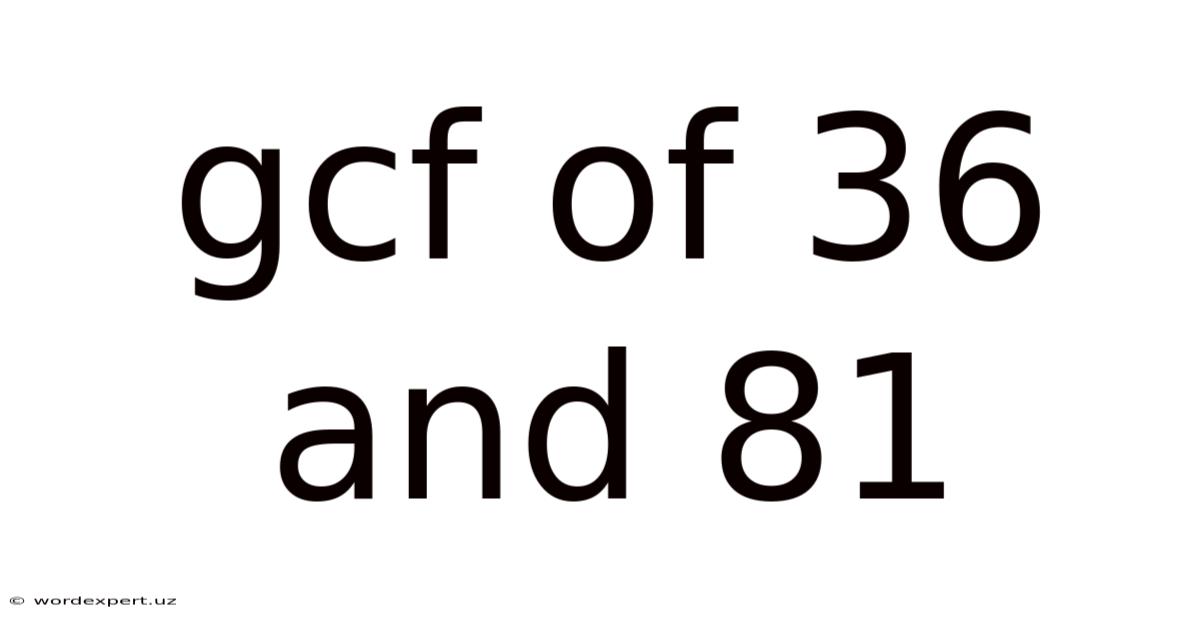
Table of Contents
Finding the Greatest Common Factor (GCF) of 36 and 81: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. Understanding GCF is crucial for simplifying fractions, solving algebraic equations, and tackling more advanced mathematical problems. This comprehensive guide will delve into the various methods for determining the GCF of 36 and 81, explaining the underlying principles and providing a deeper understanding of this important mathematical operation. We'll explore multiple approaches, ensuring you grasp the concept thoroughly and can apply it to any pair of numbers.
Understanding Greatest Common Factor (GCF)
Before we jump into calculating the GCF of 36 and 81, let's establish a firm understanding of what the GCF represents. The GCF of two or more numbers is the largest number that divides evenly into all of them without leaving a remainder. In simpler terms, it's the biggest number that's a factor of both numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The GCF of 12 and 18 is 6 because it's the largest number that divides both 12 and 18 without a remainder.
Method 1: Listing Factors
The most straightforward method for finding the GCF, especially for smaller numbers like 36 and 81, is to list all the factors of each number and then identify the largest common factor.
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Factors of 81: 1, 3, 9, 27, 81
By comparing the two lists, we can see that the common factors are 1, 3, and 9. The greatest of these common factors is 9.
Therefore, the GCF of 36 and 81 is 9.
Method 2: Prime Factorization
Prime factorization is a more powerful method that works efficiently for larger numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves. Let's apply this method to 36 and 81.
Prime Factorization of 36:
36 can be broken down as follows:
- 36 = 2 x 18
- 18 = 2 x 9
- 9 = 3 x 3
Therefore, the prime factorization of 36 is 2² x 3².
Prime Factorization of 81:
81 can be broken down as follows:
- 81 = 3 x 27
- 27 = 3 x 9
- 9 = 3 x 3
Therefore, the prime factorization of 81 is 3⁴.
Now, to find the GCF, we identify the common prime factors and take the lowest power of each. Both 36 and 81 have 3 as a prime factor. The lowest power of 3 present in both factorizations is 3².
Therefore, the GCF of 36 and 81 is 3² = 9.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, particularly useful for larger numbers where listing factors or prime factorization becomes cumbersome. This algorithm relies on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. We repeat this process until we reach a point where the two numbers are equal. That equal number is the GCF.
Let's apply the Euclidean algorithm to 36 and 81:
-
Step 1: Subtract the smaller number (36) from the larger number (81): 81 - 36 = 45. Now we find the GCF of 36 and 45.
-
Step 2: Subtract the smaller number (36) from the larger number (45): 45 - 36 = 9. Now we find the GCF of 36 and 9.
-
Step 3: Subtract the smaller number (9) from the larger number (36): 36 - 9 = 27. Now we find the GCF of 9 and 27.
-
Step 4: Subtract the smaller number (9) from the larger number (27): 27 - 9 = 18. Now we find the GCF of 9 and 18.
-
Step 5: Subtract the smaller number (9) from the larger number (18): 18 - 9 = 9. Now we find the GCF of 9 and 9.
Since both numbers are now 9, the GCF of 36 and 81 is 9.
A more concise version of the Euclidean algorithm involves repeated division with remainder:
-
Divide the larger number (81) by the smaller number (36): 81 ÷ 36 = 2 with a remainder of 9.
-
Replace the larger number with the smaller number (36) and the smaller number with the remainder (9).
-
Divide 36 by 9: 36 ÷ 9 = 4 with a remainder of 0.
When the remainder is 0, the last non-zero remainder (which is 9) is the GCF.
Understanding the Significance of GCF
The GCF plays a vital role in various mathematical operations:
-
Simplifying Fractions: The GCF allows us to simplify fractions to their lowest terms. For example, the fraction 36/81 can be simplified by dividing both the numerator and denominator by their GCF, which is 9. This simplifies the fraction to 4/9.
-
Solving Algebraic Equations: GCF is crucial in factoring algebraic expressions, which is essential for solving many types of equations.
-
Real-World Applications: GCF has practical applications in areas like tiling, arranging objects in rows and columns, and dividing resources fairly.
Frequently Asked Questions (FAQ)
-
What if the GCF is 1? If the GCF of two numbers is 1, it means the numbers are relatively prime or coprime. They share no common factors other than 1.
-
Can the GCF be larger than either of the numbers? No, the GCF can never be larger than either of the numbers. It's always less than or equal to the smaller of the two numbers.
-
Which method is best for finding the GCF? The best method depends on the numbers involved. For small numbers, listing factors is simple and straightforward. For larger numbers, prime factorization or the Euclidean algorithm is more efficient.
Conclusion
Finding the greatest common factor of 36 and 81, as demonstrated through various methods, highlights the importance of understanding fundamental mathematical concepts. Whether you employ the method of listing factors, prime factorization, or the Euclidean algorithm, the result remains consistent: the GCF of 36 and 81 is 9. Mastering these techniques will not only enhance your understanding of number theory but will also prove invaluable in solving more complex mathematical problems and tackling real-world applications. The ability to efficiently determine the GCF is a cornerstone of mathematical proficiency, applicable across numerous fields and levels of mathematical study. Remember to choose the method that best suits the numbers you are working with to find the GCF efficiently and accurately.
Latest Posts
Latest Posts
-
How To Find Other Endpoint
Sep 23, 2025
-
Cuantas Libras Tiene Un Galon
Sep 23, 2025
-
How To Find Cylinder Volume
Sep 23, 2025
-
Como Se Mide Pies Cuadrados
Sep 23, 2025
-
How Much Is 15 Milliliters
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 36 And 81 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.