Gcf Of 54 And 42
wordexpert
Sep 14, 2025 · 5 min read
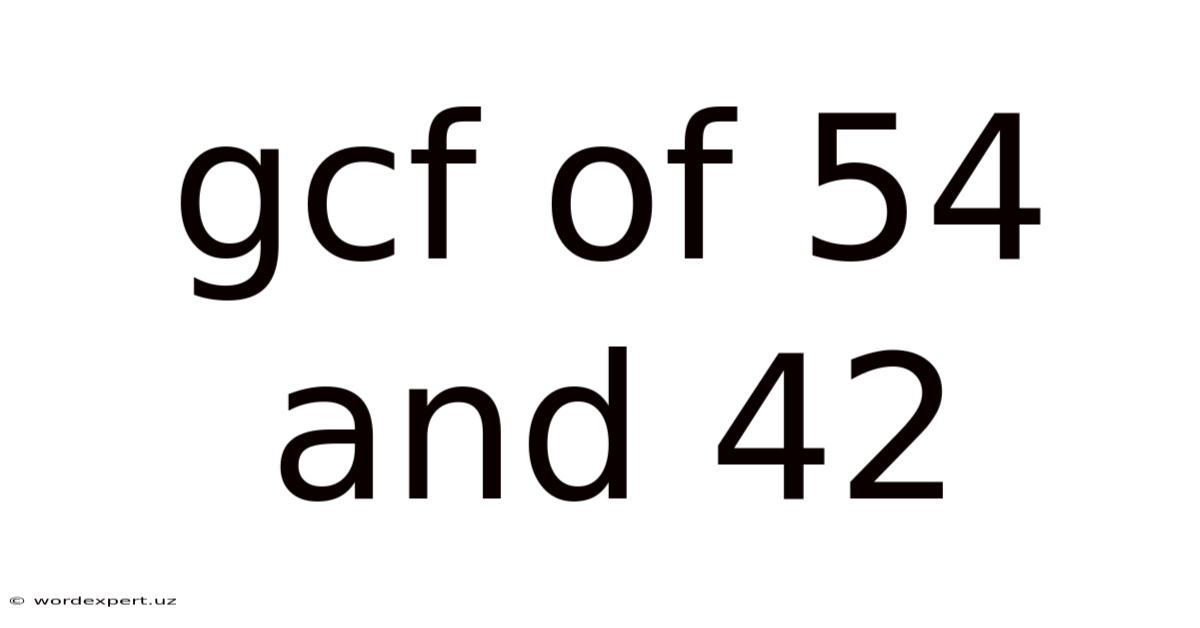
Table of Contents
Finding the Greatest Common Factor (GCF) of 54 and 42: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the highest common factor (HCF) or greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics. This guide will walk you through several methods to determine the GCF of 54 and 42, explaining the underlying principles and providing a deeper understanding of this important mathematical operation. We'll explore different approaches, from prime factorization to the Euclidean algorithm, ensuring you grasp the concepts thoroughly.
Understanding Greatest Common Factor (GCF)
Before diving into the calculation, let's solidify our understanding of what the GCF represents. The GCF of two or more numbers is the largest number that divides each of them without leaving a remainder. For example, the GCF of 12 and 18 is 6 because 6 is the largest number that divides both 12 and 18 evenly. This concept is crucial in various mathematical applications, including simplifying fractions, solving algebraic equations, and understanding number theory.
Method 1: Prime Factorization
This method involves breaking down each number into its prime factors—numbers divisible only by 1 and themselves. The GCF is then found by identifying the common prime factors and multiplying them together.
Steps:
-
Find the prime factorization of 54: 54 = 2 x 27 = 2 x 3 x 9 = 2 x 3 x 3 x 3 = 2 x 3³
-
Find the prime factorization of 42: 42 = 2 x 21 = 2 x 3 x 7
-
Identify common prime factors: Both 54 and 42 share a prime factor of 2 and a prime factor of 3.
-
Calculate the GCF: Multiply the common prime factors together: 2 x 3 = 6.
Therefore, the GCF of 54 and 42 is 6.
Method 2: Listing Factors
This method is straightforward but can be less efficient for larger numbers. It involves listing all the factors of each number and then identifying the largest common factor.
Steps:
-
List the factors of 54: 1, 2, 3, 6, 9, 18, 27, 54
-
List the factors of 42: 1, 2, 3, 6, 7, 14, 21, 42
-
Identify common factors: The common factors of 54 and 42 are 1, 2, 3, and 6.
-
Determine the GCF: The largest common factor is 6.
Therefore, the GCF of 54 and 42 is 6.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, and that number is the GCF.
Steps:
-
Start with the larger number (54) and the smaller number (42).
-
Divide the larger number by the smaller number and find the remainder: 54 ÷ 42 = 1 with a remainder of 12.
-
Replace the larger number with the smaller number (42) and the smaller number with the remainder (12).
-
Repeat the division: 42 ÷ 12 = 3 with a remainder of 6.
-
Repeat the process: 12 ÷ 6 = 2 with a remainder of 0.
-
The last non-zero remainder is the GCF. In this case, the last non-zero remainder is 6.
Therefore, the GCF of 54 and 42 is 6.
A Deeper Dive into the Euclidean Algorithm
The Euclidean algorithm's efficiency stems from its iterative nature. It systematically reduces the problem size until a trivial case is reached. The algorithm relies on the property that gcd(a, b) = gcd(b, a mod b), where a mod b represents the remainder when a is divided by b. This property ensures that the GCF remains invariant throughout the iterative process. This method avoids the need for prime factorization, making it particularly useful for large numbers where prime factorization can be computationally expensive.
Applications of GCF
The GCF has numerous applications across various mathematical fields and practical scenarios:
-
Simplifying Fractions: The GCF is used to simplify fractions to their lowest terms. For example, the fraction 54/42 can be simplified to 9/7 by dividing both the numerator and the denominator by their GCF, which is 6.
-
Algebra: GCF is essential in factoring algebraic expressions. Finding the GCF of terms allows us to simplify and solve equations more easily.
-
Number Theory: GCF plays a crucial role in number theory, forming the basis for concepts like modular arithmetic and the study of Diophantine equations.
-
Real-World Applications: GCF finds applications in various real-world problems such as dividing objects into equal groups, determining the largest possible size for tiles to cover a rectangular area without any cuts, or finding the common rhythm or pattern in music.
Frequently Asked Questions (FAQ)
Q: What if the GCF of two numbers is 1?
A: If the GCF of two numbers is 1, the numbers are called relatively prime or coprime. This means they share no common factors other than 1.
Q: Can the Euclidean algorithm be used for more than two numbers?
A: Yes, but it requires a slightly modified approach. You would first find the GCF of two numbers, and then find the GCF of that result and the next number, and so on.
Q: Is there a fastest method to find the GCF?
A: For smaller numbers, listing factors or prime factorization might be quicker. However, for larger numbers, the Euclidean algorithm is generally the most efficient. Its computational complexity is significantly lower than that of prime factorization for large numbers.
Q: Why is the GCF important in simplifying fractions?
A: Simplifying fractions using the GCF ensures the fraction is expressed in its simplest form, making it easier to understand and work with. It avoids unnecessary complexity in calculations and comparisons.
Conclusion
Finding the greatest common factor (GCF) is a fundamental mathematical skill with wide-ranging applications. This guide has explored three different methods—prime factorization, listing factors, and the Euclidean algorithm—to calculate the GCF, highlighting the strengths and weaknesses of each approach. Understanding these methods not only equips you with the ability to find the GCF but also provides a deeper appreciation for the underlying principles of number theory and its practical relevance in various mathematical contexts. Regardless of the method you choose, the GCF of 54 and 42 remains consistently 6. Mastering these techniques will undoubtedly strengthen your mathematical foundation and problem-solving abilities.
Latest Posts
Latest Posts
-
How Much Longer Until 4 30
Sep 14, 2025
-
Tirzepatide Reconstitution Calculator Online Free
Sep 14, 2025
-
Chinese Age Calculator Lunar Age
Sep 14, 2025
-
90 Days From April 16
Sep 14, 2025
-
Convert 80 Km To Miles
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 54 And 42 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.