Is 100 A Perfect Square
wordexpert
Sep 11, 2025 · 6 min read
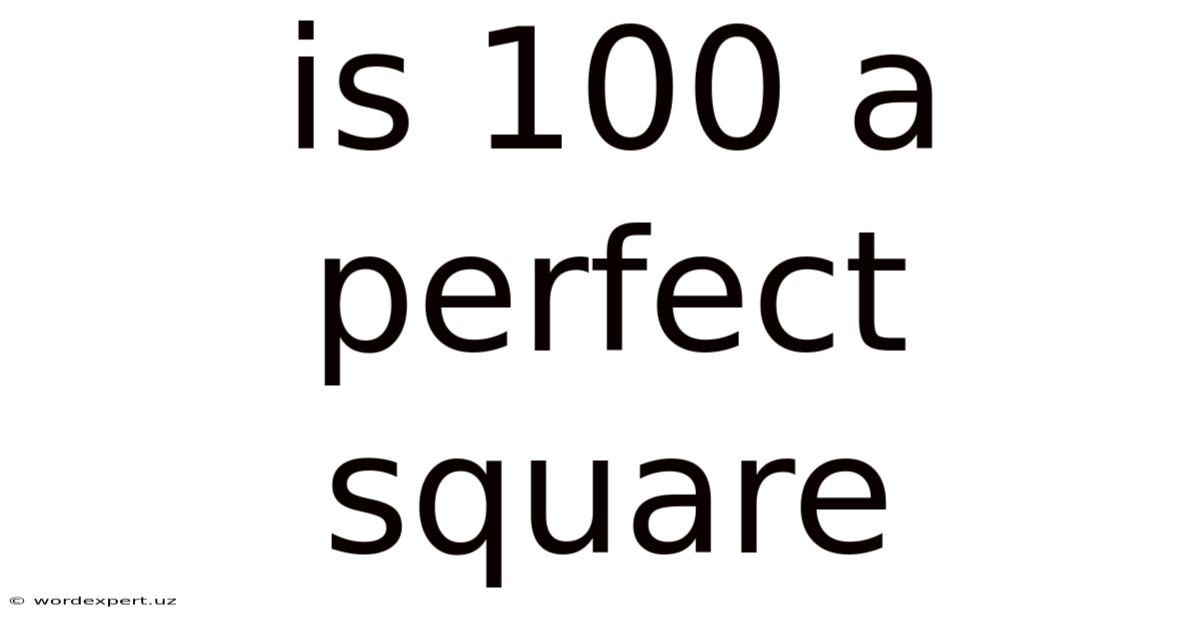
Table of Contents
Is 100 a Perfect Square? A Deep Dive into Square Numbers and Their Properties
Is 100 a perfect square? The short answer is a resounding yes. But understanding why 100 is a perfect square opens the door to a fascinating exploration of number theory, mathematical properties, and the very nature of perfect squares themselves. This article will delve into the concept of perfect squares, examining their definition, properties, and providing practical examples, all while answering the initial question comprehensively and exploring related mathematical concepts.
Understanding Perfect Squares
A perfect square, in its simplest definition, is a number that can be obtained by squaring (multiplying by itself) an integer. In other words, it's the result of multiplying a whole number by itself. For instance, 9 is a perfect square because it's the result of 3 x 3 (3 squared, or 3²). Similarly, 16 is a perfect square (4 x 4 or 4²), 25 is a perfect square (5 x 5 or 5²), and so on.
The key takeaway here is the concept of integer multiplication. We're not dealing with decimals or fractions; only whole numbers are considered when determining if a number is a perfect square. This constraint is crucial because it defines the specific set of numbers we are working with.
Why 100 is a Perfect Square
Now, let's address the main question directly: Is 100 a perfect square? Yes, it is. This is because 100 can be expressed as the square of an integer: 10 x 10 = 100 (or 10² = 100). The number 10, a whole number, when multiplied by itself, results in 100. This fulfills the definition of a perfect square.
Identifying Perfect Squares: Methods and Techniques
Several methods can be employed to determine whether a given number is a perfect square. Let's explore some of these:
-
Prime Factorization: This is a powerful technique for determining whether a number is a perfect square. Prime factorization involves breaking down a number into its prime factors (prime numbers that multiply to give the original number). If each prime factor appears an even number of times, the number is a perfect square.
Let's illustrate this with 100:
100 = 10 x 10 = (2 x 5) x (2 x 5) = 2² x 5²
Notice that both 2 and 5 appear twice (even number of times). This confirms that 100 is a perfect square.
-
Square Root Calculation: Another straightforward method involves calculating the square root of the number. If the square root is an integer, the number is a perfect square. The square root of 100 is 10, which is an integer. Therefore, 100 is a perfect square.
-
Pattern Recognition: With practice, you can start recognizing perfect squares. The first few perfect squares are 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, and so on. While this isn't a rigorous mathematical method, it can be useful for quickly identifying smaller perfect squares.
Properties of Perfect Squares
Perfect squares possess several interesting mathematical properties:
-
Even Number of Factors: Perfect squares always have an odd number of factors. This stems from the nature of their prime factorization. Since each prime factor appears an even number of times, the total number of factors will always be odd. For example, the factors of 100 are 1, 2, 4, 5, 10, 20, 25, 50, and 100 – a total of nine factors (an odd number).
-
Last Digit Pattern: The last digit of a perfect square can only be 0, 1, 4, 5, 6, or 9. This property can be used as a quick check, although it doesn't definitively prove a number is a perfect square. For instance, a number ending in 2, 3, 7, or 8 cannot be a perfect square.
-
Difference between Consecutive Perfect Squares: The difference between consecutive perfect squares always increases by 2. For example:
4 - 1 = 3 9 - 4 = 5 16 - 9 = 7 25 - 16 = 9 ...and so on.
-
Sum of Odd Numbers: Every perfect square can be expressed as the sum of consecutive odd numbers. For example:
1 = 1 4 = 1 + 3 9 = 1 + 3 + 5 16 = 1 + 3 + 5 + 7 25 = 1 + 3 + 5 + 7 + 9 ...and so on.
Applications of Perfect Squares
Understanding perfect squares is essential in various mathematical areas and real-world applications:
-
Geometry: Perfect squares are fundamental in geometry, particularly when calculating areas of squares and other related shapes. The area of a square is simply the square of its side length.
-
Algebra: Perfect squares play a vital role in solving quadratic equations and simplifying algebraic expressions. Techniques like completing the square rely heavily on the properties of perfect squares.
-
Number Theory: Perfect squares are a central theme in number theory, with many theorems and concepts built upon their properties. For instance, the study of Diophantine equations often involves perfect squares.
-
Computer Science: Algorithms related to sorting and searching often use concepts related to perfect squares for optimization purposes.
Advanced Concepts Related to Perfect Squares
Beyond the basics, there are more advanced mathematical concepts intertwined with perfect squares:
-
Pythagorean Theorem: The Pythagorean theorem, a cornerstone of geometry, states that in a right-angled triangle, the square of the hypotenuse (the longest side) is equal to the sum of the squares of the other two sides. This theorem heavily utilizes the concept of perfect squares.
-
Sum of Squares: Exploring the possibilities of expressing a number as the sum of two or more squares is a rich area of number theory. Fermat's Theorem on the Sum of Two Squares is a notable example.
-
Perfect Square Trinomials: In algebra, a perfect square trinomial is a trinomial (a polynomial with three terms) that can be factored into a perfect square. Recognizing and factoring perfect square trinomials is crucial for solving certain types of algebraic equations.
Frequently Asked Questions (FAQ)
-
Q: Are all even numbers perfect squares? A: No. Many even numbers are not perfect squares (e.g., 2, 6, 10, 14).
-
Q: Are all odd numbers perfect squares? A: No. Many odd numbers are not perfect squares (e.g., 3, 5, 7, 11).
-
Q: How can I find the next perfect square after 100? A: The next perfect square is 121 (11²). You can find subsequent perfect squares by squaring consecutive integers.
-
Q: Is zero a perfect square? A: Yes, 0 is a perfect square because 0 x 0 = 0.
-
Q: Are negative numbers perfect squares? A: No, in the context of standard real numbers, negative numbers do not have real square roots. However, in the complex number system, negative numbers have square roots involving the imaginary unit i.
Conclusion
In conclusion, 100 is indeed a perfect square, as it's the square of the integer 10. Understanding this simple fact opens the door to a deeper exploration of the fascinating world of number theory and its numerous applications. From prime factorization to geometric applications, the concept of perfect squares is pervasive throughout mathematics and its related fields. By exploring the properties and applications discussed in this article, you've not only answered the initial question but also gained a richer understanding of a fundamental mathematical concept. The exploration of perfect squares offers a rewarding journey into the beauty and elegance of numbers.
Latest Posts
Latest Posts
-
Gpm To Pounds Per Hour
Sep 11, 2025
-
Subwoofer Box For 12 Inch
Sep 11, 2025
-
Cuantos Cm Es Un Metro
Sep 11, 2025
-
Ohio Used Car Sales Tax
Sep 11, 2025
-
How Much Is 1 5 Ml
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Is 100 A Perfect Square . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.