Is 24 A Perfect Square
wordexpert
Sep 17, 2025 · 5 min read
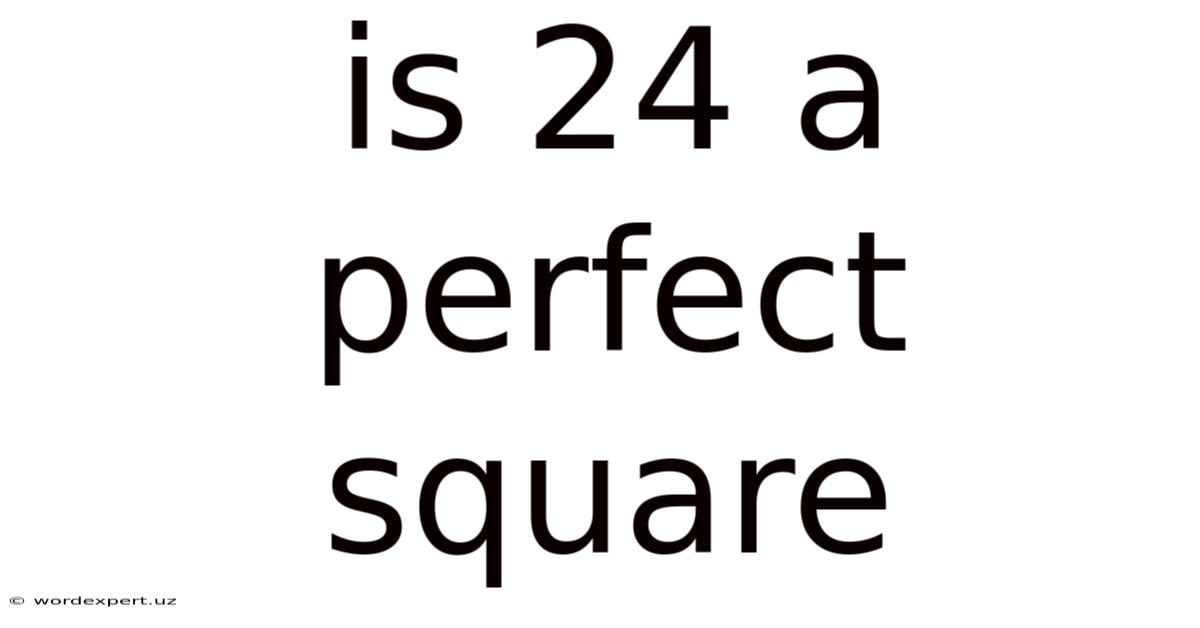
Table of Contents
Is 24 a Perfect Square? Exploring Square Numbers and Their Properties
Is 24 a perfect square? This seemingly simple question opens the door to a fascinating exploration of number theory, specifically the concept of perfect squares and their properties. Understanding perfect squares is fundamental to various mathematical concepts, from algebra to geometry and beyond. This article will definitively answer whether 24 is a perfect square, explain what constitutes a perfect square, and delve into related mathematical concepts. We’ll also address some frequently asked questions to ensure a comprehensive understanding.
Understanding Perfect Squares
A perfect square, also known as a square number, is an integer that can be obtained by squaring another integer. In simpler terms, it's the result of multiplying an integer by itself. For example:
- 1 x 1 = 1 (1 is a perfect square)
- 2 x 2 = 4 (4 is a perfect square)
- 3 x 3 = 9 (9 is a perfect square)
- 4 x 4 = 16 (16 is a perfect square)
- and so on...
Mathematically, a perfect square n can be expressed as n = k², where k is an integer. The integer k is called the square root of n.
Determining if 24 is a Perfect Square
Now, let's address the central question: Is 24 a perfect square? The answer is a definitive no. There is no integer that, when multiplied by itself, equals 24.
To illustrate this, let's consider the integers surrounding the square root of 24:
- 4 x 4 = 16
- 5 x 5 = 25
As you can see, 24 falls between two consecutive perfect squares, 16 and 25. This conclusively proves that 24 is not a perfect square.
Exploring Square Roots and Their Properties
Understanding square roots is crucial to grasping the concept of perfect squares. The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 25 is 5 because 5 x 5 = 25. The square root of a number n is denoted as √n.
While the square root of a perfect square is always an integer, the square root of a non-perfect square, like 24, is an irrational number. Irrational numbers cannot be expressed as a simple fraction and have decimal representations that continue indefinitely without repeating. The square root of 24 is approximately 4.898979..., an irrational number.
Visualizing Perfect Squares: Geometric Representation
Perfect squares have a neat geometric interpretation. Imagine arranging dots or squares into a grid. A perfect square can be represented as a square arrangement of dots or squares where the number of rows and columns are equal.
- For example, the perfect square 9 can be visualized as a 3x3 grid of dots:
* * *
* * *
* * *
This geometric representation highlights the relationship between perfect squares and area. The area of a square with side length k is k², which is a perfect square.
Perfect Squares and Number Patterns
Perfect squares exhibit interesting patterns in their numerical properties:
-
Differences between consecutive perfect squares: The difference between consecutive perfect squares increases by 2 each time. For instance:
- 4 - 1 = 3
- 9 - 4 = 5
- 16 - 9 = 7
- 25 - 16 = 9 and so on. This pattern is due to the algebraic identity (n+1)² - n² = 2n + 1.
-
Sum of odd numbers: Every perfect square can be expressed as the sum of consecutive odd numbers. For example:
- 1 = 1
- 4 = 1 + 3
- 9 = 1 + 3 + 5
- 16 = 1 + 3 + 5 + 7 and so on. This pattern reflects the visual representation of perfect squares as increasingly larger squares built from layers of odd numbers of dots.
-
Digit patterns: While less predictable, the last digits of perfect squares follow a specific pattern (0, 1, 4, 5, 6, 9). This is because the last digit of a number determines the last digit of its square.
Perfect Squares in Real-World Applications
Perfect squares have practical applications in various fields:
-
Geometry: Calculating areas and volumes of squares, cubes, and other geometric shapes frequently involves perfect squares.
-
Construction: Layout planning, building designs, and material calculations often utilize the properties of perfect squares.
-
Computer science: Algorithms and data structures, such as matrix operations and hashing, leverage concepts related to perfect squares.
-
Physics: Formulas in physics, especially in areas like optics and mechanics, sometimes involve perfect squares.
Beyond Perfect Squares: Higher Powers
The concept of perfect squares extends to higher powers as well. A perfect cube is the result of multiplying an integer by itself three times (e.g., 8 = 2³). Similarly, a perfect fourth power results from multiplying an integer by itself four times, and so on. These higher powers also possess unique mathematical properties and applications.
Frequently Asked Questions (FAQ)
Q: How do I find the square root of a number?
A: For perfect squares, you can often recognize the square root through memorization or simple calculation. For other numbers, you can use a calculator or employ numerical methods to approximate the square root.
Q: Are all integers perfect squares?
A: No, only a relatively small subset of integers are perfect squares. Most integers are not perfect squares.
Q: What is the difference between a perfect square and a square root?
A: A perfect square is the result of squaring an integer, while the square root is the original integer that was squared. They are inverse operations.
Q: Are there any formulas to directly determine if a number is a perfect square?
A: There isn't a single, simple formula to directly determine if a large number is a perfect square. However, methods like prime factorization or checking for patterns in the number's properties can help. Efficient algorithms exist for large-scale verification.
Q: What are some applications of perfect squares beyond those mentioned above?
A: Perfect squares and their generalizations find applications in cryptography, coding theory, and various areas of abstract algebra.
Conclusion
In conclusion, 24 is definitively not a perfect square. This exploration has provided a deeper understanding of perfect squares, their properties, and their significance within mathematics and various real-world applications. Understanding perfect squares is a stepping stone to appreciating more complex mathematical concepts and their practical uses. From the simple act of squaring a number to its far-reaching implications in diverse fields, the concept of perfect squares reveals a rich and fascinating aspect of the mathematical world. This understanding lays a foundation for further exploration into number theory and its applications.
Latest Posts
Latest Posts
-
Convertidor De Pulgadas A Metros
Sep 17, 2025
-
Car Sales Tax Missouri Calculator
Sep 17, 2025
-
How Long Is 69 Weeks
Sep 17, 2025
-
How Much Is 3000 Pennies
Sep 17, 2025
-
How Much Longer Until 2
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Is 24 A Perfect Square . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.