Is 6 A Perfect Square
wordexpert
Sep 21, 2025 · 6 min read
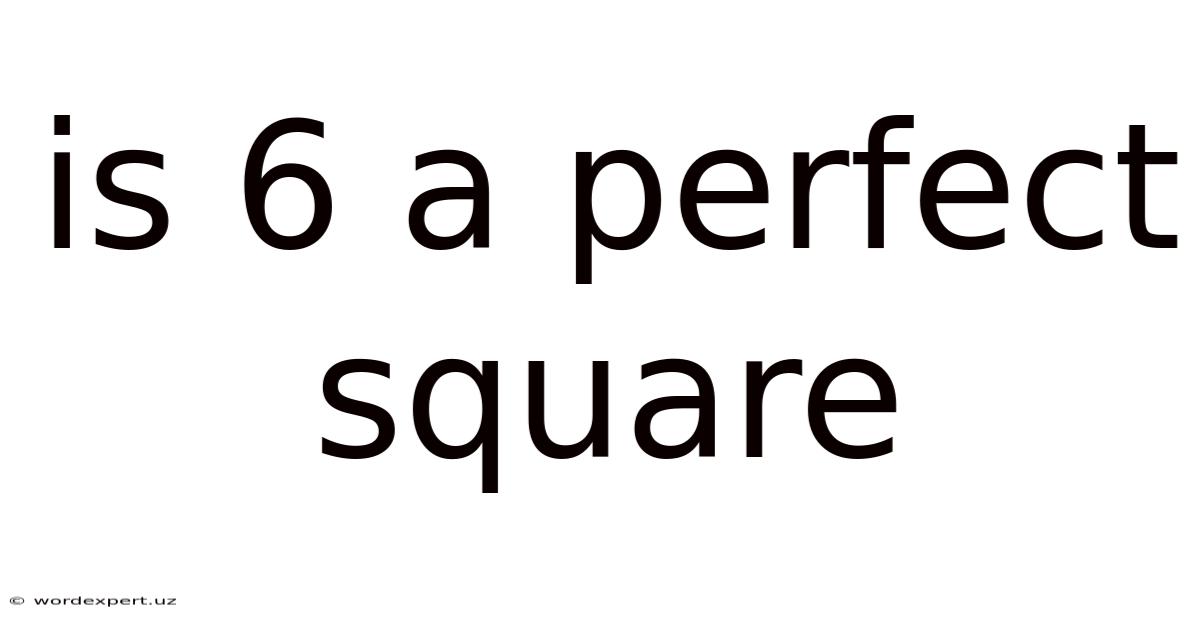
Table of Contents
Is 6 a Perfect Square? Exploring Square Numbers and Their Properties
Is 6 a perfect square? This seemingly simple question opens the door to a fascinating exploration of number theory, specifically the concept of perfect squares and their properties. The short answer is no, 6 is not a perfect square. But understanding why requires delving into the definition of perfect squares and examining their characteristics. This article will not only answer the question definitively but will also provide a comprehensive understanding of perfect squares, their identification, and their relevance in mathematics.
Understanding Perfect Squares
A perfect square is a number that can be obtained by squaring (multiplying by itself) an integer. In simpler terms, it's the result of multiplying a whole number by itself. For example:
- 1 x 1 = 1 (1 is a perfect square)
- 2 x 2 = 4 (4 is a perfect square)
- 3 x 3 = 9 (9 is a perfect square)
- 4 x 4 = 16 (16 is a perfect square)
- and so on...
The sequence of perfect squares continues infinitely: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, and so forth. Notice that each number in this sequence can be expressed as the square of an integer.
Why 6 is Not a Perfect Square
To determine if 6 is a perfect square, we need to find an integer that, when multiplied by itself, equals 6. Let's try some possibilities:
- 1 x 1 = 1
- 2 x 2 = 4
- 3 x 3 = 9
We see that there is no whole number that, when squared, results in 6. The square root of 6 is approximately 2.449, which is not an integer. This definitively proves that 6 is not a perfect square.
Exploring the Properties of Perfect Squares
Understanding why 6 isn't a perfect square leads us to explore the more profound properties of these numbers. These properties are crucial in various areas of mathematics, including algebra, geometry, and number theory.
1. Even and Odd Perfect Squares:
Observe the sequence of perfect squares: 1, 4, 9, 16, 25, 36... Notice a pattern? The squares of even numbers (2, 4, 6...) are always even, and the squares of odd numbers (1, 3, 5...) are always odd. This is because when you multiply an even number by itself, the result is always even. Similarly, multiplying an odd number by itself always results in an odd number.
2. The Last Digit Pattern of Perfect Squares:
Another interesting property lies in the last digit of perfect squares. The last digit of a perfect square can only be one of these digits: 0, 1, 4, 5, 6, or 9. This is a useful tool for quickly determining if a large number might be a perfect square. If the last digit isn't one of these six, then the number cannot be a perfect square. For example, a number ending in 2, 3, 7, or 8 cannot be a perfect square.
3. Perfect Squares and Prime Factorization:
Prime factorization is the process of expressing a number as a product of its prime factors. Perfect squares have a unique property in their prime factorization: each prime factor appears an even number of times. For example:
- 36 = 2² x 3² (Both 2 and 3 appear twice)
- 100 = 2² x 5² (Both 2 and 5 appear twice)
If a number's prime factorization contains any prime factor with an odd exponent, then it cannot be a perfect square. Let's examine the prime factorization of 6:
- 6 = 2 x 3
Since both 2 and 3 appear only once (exponent of 1), 6 does not satisfy the condition for a perfect square.
4. Geometric Representation of Perfect Squares:
Perfect squares have a beautiful geometric interpretation. They can be represented as square arrays of dots or unit squares. For example, the perfect square 9 can be arranged as a 3x3 square:
* * *
* * *
* * *
This visual representation highlights the concept of squaring a number – creating a square array with side length equal to the original number.
5. Perfect Squares in Pythagorean Theorem:
Perfect squares play a fundamental role in the Pythagorean theorem, a cornerstone of geometry. The theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. This relationship heavily relies on the concept of perfect squares.
Beyond the Basics: Square Roots and Irrational Numbers
The question of whether 6 is a perfect square naturally leads to the concept of square roots. The square root of a number is a value that, when multiplied by itself, gives the original number. While some numbers have integer square roots (perfect squares), others do not. The square root of 6, denoted as √6, is an irrational number. Irrational numbers cannot be expressed as a simple fraction and have decimal representations that continue infinitely without repeating.
Frequently Asked Questions (FAQ)
Q: Are there any other numbers that are not perfect squares?
A: Yes, the vast majority of numbers are not perfect squares. Only a relatively small subset of numbers are perfect squares. Any number that doesn't have a whole number as its square root is not a perfect square.
Q: How can I quickly determine if a large number is a perfect square?
A: Check the last digit. If it's not 0, 1, 4, 5, 6, or 9, it's not a perfect square. You can also use prime factorization. If any prime factor appears an odd number of times, it’s not a perfect square. Calculators and computer programs can efficiently compute square roots to determine if a number is a perfect square.
Q: What is the importance of perfect squares in mathematics?
A: Perfect squares are fundamental building blocks in various mathematical fields. They are crucial in algebra (solving quadratic equations), geometry (Pythagorean theorem, area calculations), and number theory (Diophantine equations, modular arithmetic). Their properties and relationships with other numbers are extensively studied.
Q: What are some real-world applications of perfect squares?
A: Perfect squares appear in various real-world applications, from calculating areas and volumes (e.g., finding the area of a square tile) to more advanced concepts in physics and engineering (e.g., calculating energy levels in quantum mechanics).
Conclusion
In conclusion, 6 is definitively not a perfect square. This seemingly simple question has served as a gateway to explore a rich and fascinating area of mathematics. Understanding perfect squares and their properties is crucial for grasping fundamental concepts in number theory, algebra, and geometry. Their unique characteristics and patterns provide a deeper appreciation for the intricacies and beauty inherent within the world of numbers. By exploring the "why" behind the answer, we've gained a more profound understanding of the mathematical landscape.
Latest Posts
Latest Posts
-
How Long Is 79 Days
Sep 21, 2025
-
200 Ml To Cups Water
Sep 21, 2025
-
Punnett Square Eye Color Calculator
Sep 21, 2025
-
How To Calculate Engine Capacity
Sep 21, 2025
-
Acid Test Quick Ratio Calculator
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Is 6 A Perfect Square . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.