Is -6 Greater Than -4
wordexpert
Sep 23, 2025 · 5 min read
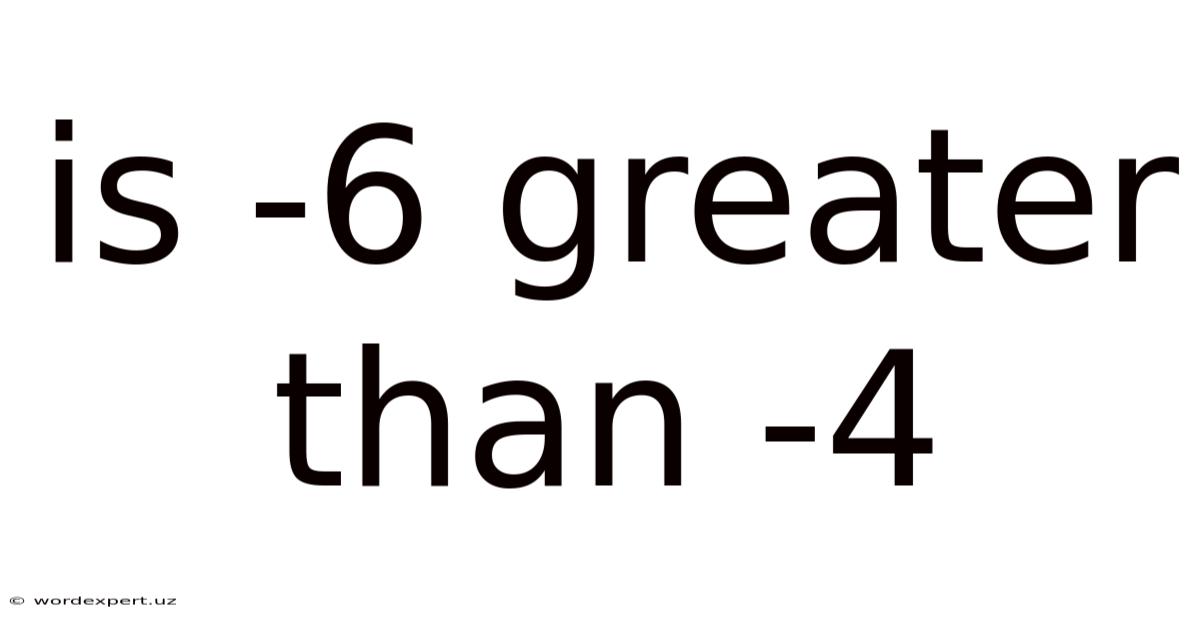
Table of Contents
Is -6 Greater Than -4? Understanding Negative Numbers
This seemingly simple question, "Is -6 greater than -4?", often trips up students first encountering negative numbers. Understanding the concept of negative numbers and their relationship on the number line is crucial for mastering basic arithmetic and algebra. This article will delve deep into the concept, exploring not only the answer to this question but also the underlying principles of comparing negative numbers, offering practical examples and addressing common misconceptions. We'll explore the number line, different representations of negative numbers, and provide a solid foundation for understanding this fundamental mathematical concept.
Understanding the Number Line
The number line provides a visual representation of numbers, extending infinitely in both positive and negative directions. Zero sits in the middle, with positive numbers increasing to the right and negative numbers decreasing to the left. Imagine it as a horizontal ruler, but instead of just measuring lengths, it measures values.
- Zero (0): The point of origin, separating positive and negative numbers.
- Positive Numbers (+): Numbers greater than zero, located to the right of zero on the number line.
- Negative Numbers (-): Numbers less than zero, located to the left of zero on the number line.
When comparing numbers on the number line, the number further to the right is always greater. This principle holds true for both positive and negative numbers.
Comparing Negative Numbers: The Key Concept
The key to understanding the comparison of negative numbers lies in grasping that the further a number is to the left of zero on the number line, the smaller it is. This contrasts with our intuitive understanding of positive numbers, where larger numbers are further to the right.
Let's illustrate this with our example: -6 and -4.
- -4: Located to the right of -6 on the number line.
- -6: Located to the left of -4 on the number line.
Since -4 is to the right of -6 on the number line, -4 is greater than -6. Therefore, the answer to the question "Is -6 greater than -4?" is no. -4 is greater than -6.
Visualizing with a Number Line: A Step-by-Step Guide
Let's visualize this with a simple number line:
-8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8
Notice how -4 is positioned to the right of -6. This visual representation reinforces the concept that -4 is larger than -6.
Real-World Applications of Negative Numbers
Negative numbers aren't just abstract mathematical concepts; they have practical applications in various real-world scenarios:
- Temperature: Temperatures below zero degrees Celsius (or Fahrenheit) are represented by negative numbers. For example, -10°C is colder (and therefore smaller) than -5°C.
- Finance: Negative numbers represent debts or deficits. A bank account with a balance of -$500 represents a larger debt than an account with a balance of -$100.
- Elevation: Elevations below sea level are represented by negative numbers. A location -100 meters below sea level is lower (and therefore smaller) than a location -50 meters below sea level.
- Coordinates: In Cartesian coordinates, negative numbers indicate positions along the negative x or y axes.
Debunking Common Misconceptions
Many students initially struggle with negative numbers because they contradict our intuitive understanding of numbers based on everyday experience with positive numbers. Here are some common misconceptions:
- Ignoring the Negative Sign: Students may mistakenly think that because 6 is greater than 4, -6 is also greater than -4. This is incorrect; the negative sign fundamentally changes the value's position on the number line.
- Thinking of the Absolute Value: The absolute value of a number is its distance from zero, ignoring the sign. While |-6| (6) is greater than |-4| (4), this doesn't mean -6 is greater than -4. Absolute value represents magnitude, not order on the number line.
- Confusing Magnitude with Value: A larger absolute value does not equate to a larger numerical value when considering negative numbers. -100 has a larger absolute value (100) than -10 (10), but -10 is larger than -100 on the number line.
Further Exploring Negative Numbers: Operations and Properties
Understanding the comparison of negative numbers is just the first step. Let's briefly explore some fundamental operations involving negative numbers:
- Addition: Adding a negative number is equivalent to subtracting its positive counterpart. For example, 5 + (-3) = 5 - 3 = 2.
- Subtraction: Subtracting a negative number is equivalent to adding its positive counterpart. For example, 5 - (-3) = 5 + 3 = 8.
- Multiplication and Division: The rules for multiplication and division with negative numbers are as follows:
- Positive × Positive = Positive
- Positive × Negative = Negative
- Negative × Positive = Negative
- Negative × Negative = Positive The same rules apply to division.
Frequently Asked Questions (FAQ)
Q: Why do we need negative numbers?
A: Negative numbers are essential for representing values less than zero in various real-world contexts, as discussed earlier (temperature, finance, elevation, coordinates). They complete the number system and allow for a comprehensive representation of quantities.
Q: Is -100 greater than -1?
A: No. -1 is greater than -100 because it lies to the right of -100 on the number line.
Q: How can I easily compare two negative numbers?
A: Imagine the number line. The number closer to zero is always the greater number. Alternatively, consider their absolute values; the number with the smaller absolute value will be greater.
Q: What happens when you add a positive and a negative number?
A: The result depends on the magnitudes of the numbers. If the positive number has a larger magnitude, the result will be positive. If the negative number has a larger magnitude, the result will be negative.
Conclusion: Mastering Negative Numbers
Understanding negative numbers and their relationships is a fundamental building block in mathematics. By visualizing them on a number line and understanding the key concept that numbers further to the left are smaller, you can easily compare negative numbers and confidently answer questions like "Is -6 greater than -4?". This understanding extends beyond simple comparisons, forming a crucial foundation for more advanced mathematical concepts and real-world applications. Remember to always refer to the number line for a clear visual representation and avoid common misconceptions related to absolute values and signs. With practice and consistent application, mastering negative numbers will become second nature.
Latest Posts
Latest Posts
-
90 Days After June 17
Sep 24, 2025
-
90 Days From 7 24
Sep 24, 2025
-
Cuanto Es Un Pie Cubico
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Is -6 Greater Than -4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.