Log Base 2 Of 128
wordexpert
Sep 17, 2025 · 6 min read
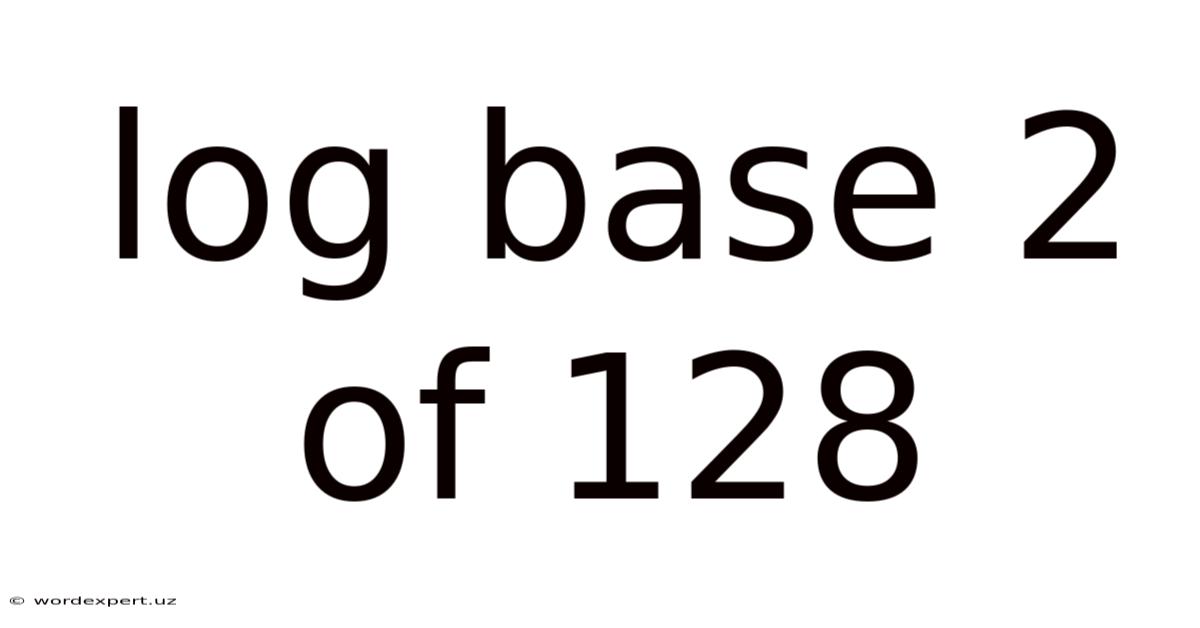
Table of Contents
Decoding the Mystery: Log₂(128) and its Implications
Understanding logarithms, especially those with base 2 (binary logarithms), is crucial in various fields, from computer science and information theory to mathematics and engineering. This article dives deep into the calculation and significance of log₂(128), providing a comprehensive explanation suitable for both beginners and those seeking a more thorough understanding. We'll explore the fundamental concepts, step-by-step calculations, real-world applications, and frequently asked questions related to this specific logarithmic expression. By the end, you'll not only know the answer to log₂(128) but also grasp the underlying principles and their wider implications.
What are Logarithms? A Gentle Introduction
Before we tackle log₂(128), let's briefly review the concept of logarithms. A logarithm is essentially the inverse operation of exponentiation. In simpler terms, if we have an equation like b<sup>x</sup> = y, then the logarithm of y with base b is x, written as log<sub>b</sub>(y) = x. This reads as: "the base-b logarithm of y is x".
Think of it like this: exponentiation asks "What is b raised to the power of x?", while the logarithm asks "To what power must we raise b to get y?".
Understanding Base 2 Logarithms (Binary Logarithms)
Base 2 logarithms, denoted as log₂(x), are logarithms with a base of 2. They are particularly important in computer science because computers operate using a binary system (base 2) – a system with only two digits: 0 and 1. In this system, each bit (binary digit) represents a power of 2. For example:
- 2⁰ = 1
- 2¹ = 2
- 2² = 4
- 2³ = 8
- 2⁴ = 16
- 2⁵ = 32
- 2⁶ = 64
- 2⁷ = 128
- and so on...
Calculating log₂(128): A Step-by-Step Approach
Now, let's calculate log₂(128). We are looking for the exponent (x) such that 2<sup>x</sup> = 128. From the powers of 2 listed above, we can directly see that 2⁷ = 128. Therefore:
log₂(128) = 7
This means that we need to raise 2 to the power of 7 to obtain 128.
Alternative Methods for Calculating Base 2 Logarithms
While the direct observation method works well for smaller numbers like 128, more complex scenarios might require different approaches. Here are a few:
- Using the Change of Base Formula: If you have a calculator that doesn't directly calculate base 2 logarithms, you can use the change of base formula:
log<sub>b</sub>(x) = log<sub>a</sub>(x) / log<sub>a</sub>(b)
Where 'a' is any other base (e.g., base 10 or the natural logarithm base e). For log₂(128), we could use:
log₂(128) = log₁₀(128) / log₁₀(2) ≈ 2.107 / 0.301 ≈ 7
- Using a Scientific Calculator: Most scientific calculators have a built-in function for logarithms. You would typically input "log₂(128)" or use the change of base formula if your calculator doesn't have a base 2 logarithm function directly.
The Significance of log₂(128) in Computer Science
The result, 7, is highly significant in computer science contexts. Let's consider some applications:
-
Bits and Bytes: The number 128 represents 128 units of information. Since each bit can represent one of two states (0 or 1), it takes 7 bits to represent 128 unique values (2⁷ = 128). This is because each additional bit doubles the number of possible combinations.
-
Memory and Storage: In computing, data is stored in bytes, where one byte is equal to 8 bits. Understanding base 2 logarithms helps determine the number of bits required to represent a certain amount of data. For instance, to represent 128 distinct values, we need 7 bits. If we consider 128 bytes, we're talking about 1024 bits (128 * 8).
-
Data Structures and Algorithms: Base 2 logarithms often appear in the analysis of algorithms' efficiency. For instance, the time complexity of a binary search algorithm is proportional to log₂(n), where 'n' is the number of elements in the sorted data set. This logarithmic time complexity makes binary search incredibly efficient for large datasets.
-
Network Addressing: In networking, IP addresses use binary representation. Understanding base 2 logarithms helps analyze the address space and number of possible addresses within a network.
Beyond the Basics: Exploring Deeper Concepts
While log₂(128) = 7 is a straightforward calculation, it serves as a gateway to understanding more complex logarithmic concepts:
-
Logarithmic Scales: Logarithmic scales are used to represent vast ranges of values, such as sound intensity (decibels) or earthquake magnitudes (Richter scale). These scales compress the data, making it easier to visualize and interpret.
-
Information Theory: In information theory, base 2 logarithms are fundamental to quantifying information content. The amount of information conveyed by an event is proportional to the base 2 logarithm of the reciprocal of the probability of that event.
-
Differential Equations: Logarithms appear frequently in the solutions to differential equations, particularly those modeling exponential growth or decay.
-
Fractals and Chaos Theory: Logarithms are used extensively in fractal geometry and chaos theory for describing self-similarity and scaling properties.
Frequently Asked Questions (FAQ)
Q: Can I use a different base to calculate log₂(128)?
A: Yes, you can use the change of base formula to calculate log₂(128) using any other base (e.g., base 10, base e). The result will always be 7.
Q: What is the significance of the base in a logarithm?
A: The base determines the exponential relationship being considered. Base 2 is crucial because it aligns directly with the binary system of computers. Other bases have their own applications in different fields.
Q: What if the number isn't a perfect power of 2?
A: If the number isn't a perfect power of 2, the logarithm will be a non-integer value. For example, log₂(100) is approximately 6.64, indicating that 2⁶ is less than 100, and 2⁷ is greater than 100.
Q: Are there any limitations to using base 2 logarithms?
A: Base 2 logarithms are best suited for situations related to binary systems and powers of 2. For applications not directly linked to binary, other bases might be more appropriate and offer simpler calculations.
Conclusion: More Than Just a Number
The seemingly simple calculation of log₂(128) = 7 reveals a wealth of information and implications, particularly within the context of computer science and related fields. Understanding base 2 logarithms is essential for grasping the fundamentals of digital information processing, data structures, algorithmic efficiency, and various other areas. This article has explored the calculation, significance, and broader applications of this logarithmic expression, providing a solid foundation for further exploration into the fascinating world of logarithms and their profound influence on various scientific and technological disciplines. While we've focused on log₂(128), the principles discussed apply to other base 2 logarithms and indeed, logarithms in general, highlighting their importance as a fundamental mathematical tool.
Latest Posts
Latest Posts
-
Month Over Month Percentage Change
Sep 17, 2025
-
8 Cups How Many Quarts
Sep 17, 2025
-
1 85 Million Divided By 11
Sep 17, 2025
-
Cuantas Libras Son 52 Kilos
Sep 17, 2025
-
One Hectare In Square Feet
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Log Base 2 Of 128 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.