Square Root Of 2 Squared
wordexpert
Sep 11, 2025 · 7 min read
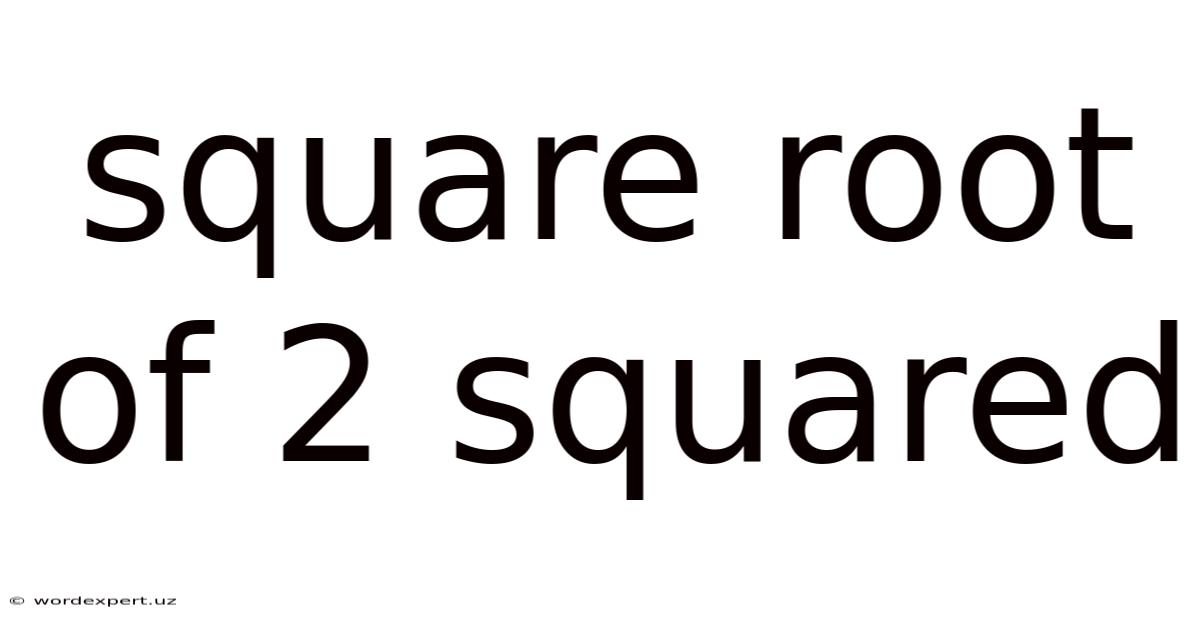
Table of Contents
Decoding the Mystery: Understanding the Square Root of 2 Squared
The seemingly simple expression, "the square root of 2 squared," often trips up students encountering it for the first time. While the answer might appear obvious at a glance, a deeper dive reveals fascinating connections to fundamental mathematical concepts, including irrational numbers, Pythagorean theorem, and the history of mathematics itself. This article will not only provide a clear explanation of the solution but also explore the rich mathematical tapestry surrounding this seemingly simple problem. We’ll unpack the concept step-by-step, demystifying the process and highlighting its broader significance.
What Does it Even Mean? Breaking Down the Expression
Before diving into the solution, let's dissect the expression: "the square root of 2 squared". This can be written mathematically as √(2²) . Let's break this down:
- 2² (two squared): This means 2 multiplied by itself: 2 x 2 = 4.
- √ (square root): This is the inverse operation of squaring. It asks the question: "What number, when multiplied by itself, equals the number under the square root symbol?"
Therefore, the expression becomes √(4). The answer, as we will see below, is relatively straightforward, but the journey to understanding it opens up a world of mathematical intrigue.
Solving the Equation: The Simple Answer
Substituting 2² with its equivalent value (4), our expression simplifies to √4. The square root of 4 is the number that, when multiplied by itself, equals 4. That number is 2. Therefore:
√(2²) = √4 = 2
This seemingly simple calculation is the foundation upon which we can build a more comprehensive understanding of the relationship between square roots and squares.
The Significance of Irrational Numbers: Beyond the Obvious
While the solution to √(2²) is a neat and tidy 2, the journey to understanding the concept of square roots, particularly the square root of 2 (√2), reveals a crucial aspect of mathematics: irrational numbers.
An irrational number is a number that cannot be expressed as a simple fraction (a ratio of two integers). While it might seem counterintuitive, many seemingly simple square roots, such as √2, are irrational. This means their decimal representation goes on forever without repeating. This concept was a groundbreaking discovery in ancient Greece, challenging the prevailing belief that all numbers could be expressed as ratios.
The discovery of the irrationality of √2 is often attributed to the Pythagorean school, a group of mathematicians and philosophers in ancient Greece. The story goes that the discovery caused a crisis within the Pythagorean community, as it challenged their fundamental beliefs about the nature of numbers and the universe.
The proof of √2's irrationality is a classic example of a proof by contradiction. It demonstrates that assuming √2 is rational leads to a logical contradiction, therefore proving it must be irrational. This proof is beyond the scope of this article but highlights the importance of rigorous mathematical proof and the sometimes surprising nature of mathematical truths.
The Pythagorean Theorem and √2: A Historic Connection
The square root of 2 is intimately linked to the Pythagorean Theorem, a cornerstone of geometry. The theorem states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (the legs). Expressed mathematically:
a² + b² = c²
Consider a right-angled triangle with legs of length 1. According to the Pythagorean Theorem:
1² + 1² = c²
1 + 1 = c²
2 = c²
Therefore, the length of the hypotenuse (c) is √2. This reveals that the square root of 2 isn't just an abstract mathematical concept; it has a real-world geometric representation as the length of the diagonal of a unit square. This connection highlights the elegant interplay between geometry and algebra within mathematics.
Understanding Square Roots: A Deeper Dive into the Concept
The square root of a number x is a number y such that y² = x. In simpler terms, it's the number that, when multiplied by itself, gives you the original number. However, we must acknowledge the existence of both positive and negative square roots. For example, both 2 and -2, when squared, result in 4. However, when we refer to "the" square root, we typically mean the positive square root (also called the principal square root).
This concept extends beyond simple numbers. We can find the square root of variables, expressions, and even complex numbers. The ability to manipulate square roots is crucial in various mathematical fields, including algebra, calculus, and trigonometry.
Expanding the Concept: Higher-Order Roots
The concept of square roots extends to higher-order roots. A cube root (∛) finds a number that, when multiplied by itself three times, gives the original number. Similarly, a fourth root finds a number that, when multiplied by itself four times, gives the original number, and so on. These higher-order roots are crucial in various mathematical and scientific applications, such as finding the roots of polynomial equations.
Practical Applications: Where do We Use Square Roots?
Square roots are not just abstract mathematical concepts; they have numerous practical applications across various fields:
- Physics: Calculating velocities, distances, and energies often involves square roots.
- Engineering: Designing structures, calculating forces, and analyzing stress require the use of square roots.
- Finance: Calculating returns on investment, determining interest rates, and valuing assets often utilize square roots.
- Computer Graphics: Generating 2D and 3D images and animations often relies heavily on square root calculations.
- Statistics: Calculating standard deviations and variances necessitate the use of square roots.
These applications showcase the fundamental role of square roots in solving real-world problems.
Common Mistakes and Misconceptions
While the calculation of √(2²) is straightforward, some common misconceptions can arise when dealing with square roots:
- Confusing squaring and square rooting: It's crucial to remember that squaring and square rooting are inverse operations, but they don't always cancel each other out exactly when dealing with negative numbers.
- Incorrect order of operations: Following the order of operations (PEMDAS/BODMAS) is crucial when dealing with complex expressions involving square roots.
- Misunderstanding irrational numbers: Many students struggle to grasp the concept of irrational numbers, which leads to difficulties in understanding square roots of non-perfect squares.
Frequently Asked Questions (FAQ)
Q: What is the difference between √(2²) and (√2)²?
A: They are equivalent. Squaring and taking the square root are inverse operations, so they effectively cancel each other out, leaving just 2.
Q: Can you explain the proof that √2 is irrational?
A: The proof is a bit complex and requires a deeper understanding of proof by contradiction. While beyond the scope of this introductory article, searching online for "proof of irrationality of √2" will yield many resources explaining this in detail.
Q: Are there other irrational numbers besides √2?
A: Yes, many numbers are irrational. Examples include π (pi) and e (Euler's number). In fact, most real numbers are irrational.
Q: What is the significance of the discovery of irrational numbers?
A: The discovery of irrational numbers was a significant moment in the history of mathematics, challenging existing beliefs about the nature of numbers and fundamentally altering our understanding of mathematical systems. It showed that some numbers cannot be perfectly represented as fractions.
Conclusion: More Than Just a Simple Calculation
The square root of 2 squared (√(2²)) might seem like a trivial problem at first glance. However, its solution unveils a fascinating world of mathematical concepts, from the basic understanding of square roots and squares to the more advanced concept of irrational numbers and their historical significance. Understanding this seemingly simple expression provides a glimpse into the rich tapestry of mathematics, showcasing the elegance and intricacy of fundamental mathematical principles and their connections to various fields of study and real-world applications. This seemingly simple calculation is a gateway to a deeper appreciation for the beauty and complexity of the mathematical world.
Latest Posts
Latest Posts
-
Ng Ml To Mg L
Sep 11, 2025
-
How Long Is 84 Weeks
Sep 11, 2025
-
How Long Is 70 Days
Sep 11, 2025
-
How Do I Calculate Enthalpy
Sep 11, 2025
-
100 Days From January 20
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Square Root Of 2 Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.