What Is 100 Of 40
wordexpert
Sep 11, 2025 · 5 min read
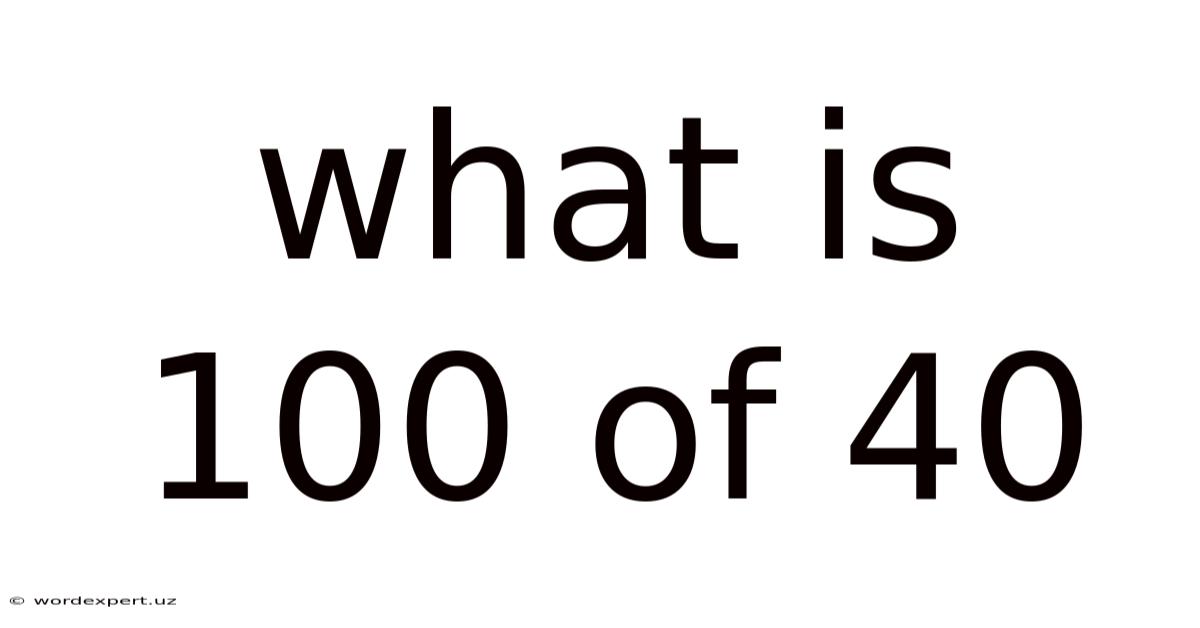
Table of Contents
What is 100% of 40? Understanding Percentages and Their Applications
Finding 100% of 40 might seem like a trivial question at first glance. However, understanding how to calculate percentages, especially the seemingly simple ones, forms the foundation for more complex mathematical concepts and real-world applications. This article will delve into the process of calculating 100% of 40, explaining the underlying principles of percentages, exploring different calculation methods, and demonstrating its relevance in various scenarios. We'll also address frequently asked questions and expand upon related concepts to provide a comprehensive understanding of percentage calculations.
Understanding Percentages: A Foundation in Fractions and Ratios
A percentage is simply a fraction or ratio expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of one hundred." Therefore, 100% represents the entirety of something – the whole. Any value expressed as a percentage shows its proportion relative to the whole.
For instance, 50% represents 50 out of 100, or one-half (1/2). Similarly, 25% is 25 out of 100, or one-quarter (1/4). Understanding this basic relationship between percentages, fractions, and ratios is key to mastering percentage calculations.
Calculating 100% of 40: The Simple Approach
The question, "What is 100% of 40?" directly translates to "What is the whole amount when 40 represents 100% of it?" The answer is straightforward: 100% of 40 is 40.
This is because 100% signifies the entire quantity. If 40 represents the whole, then 100% of that whole remains 40. There's no calculation needed in this specific case; the answer is inherent in the question's phrasing.
Different Methods for Calculating Percentages: Expanding the Knowledge
While the 100% case is simple, let's explore different methods for calculating percentages that will prove useful when dealing with more complex scenarios. These methods build upon the fundamental understanding of percentages as fractions and ratios.
Method 1: Using the Fraction Method
Every percentage can be expressed as a fraction. 100% is equivalent to 100/100, which simplifies to 1. Therefore, finding 100% of a number is the same as multiplying that number by 1.
- Formula: Percentage/100 * Number
- Application: (100/100) * 40 = 1 * 40 = 40
Method 2: Using the Decimal Method
Percentages can also be converted to decimals. To convert a percentage to a decimal, divide the percentage by 100. 100% divided by 100 is 1.0. Therefore, calculating 100% of a number is the same as multiplying that number by 1.0.
- Formula: (Percentage/100) * Number
- Application: (100/100) * 40 = 1.0 * 40 = 40
Method 3: The Proportion Method
This method uses ratios to solve percentage problems. It's particularly useful for finding an unknown percentage of a number. We set up a proportion:
- Formula: x/40 = 100/100
- Solving: Cross-multiply: 100x = 4000. Divide both sides by 100: x = 40
This method might seem more complicated for calculating 100% of 40, but it provides a framework for solving more challenging percentage problems.
Real-World Applications: Beyond the Classroom
Understanding percentage calculations, even the seemingly basic ones like finding 100% of a number, has widespread applications in various fields:
-
Finance: Calculating interest rates, discounts, taxes, and profit margins all rely heavily on percentage calculations. Understanding 100% represents the principal amount is crucial in these financial calculations.
-
Business: Analyzing sales data, market share, and growth rates involve percentages extensively. Knowing the base value (100%) is fundamental for comparative analysis.
-
Science: Expressing experimental results, statistical data, and error margins often utilize percentages.
-
Everyday Life: Calculating tips, discounts in stores, and understanding nutritional information on food labels all require a grasp of percentages.
Frequently Asked Questions (FAQ)
Q1: What if I need to find a different percentage of 40, say 25%?
To find 25% of 40, you would use any of the methods described above, substituting 25 for the percentage.
- Fraction Method: (25/100) * 40 = 0.25 * 40 = 10
- Decimal Method: 0.25 * 40 = 10
- Proportion Method: x/40 = 25/100; solving for x gives x = 10
Q2: What does it mean if a percentage is greater than 100%?
A percentage greater than 100% indicates that the part is larger than the whole. This often happens when comparing quantities over time or when considering growth. For example, if sales increased by 120% from the previous year, it signifies the current sales are 220% of the previous year's sales.
Q3: Can I use a calculator for percentage calculations?
Yes, calculators have percentage functions that simplify these calculations. Many calculators have a "%" button. However, understanding the underlying principles is still crucial for problem-solving and interpreting results.
Q4: How do I calculate percentage increase or decrease?
To calculate percentage increase: [(New Value - Original Value) / Original Value] * 100
To calculate percentage decrease: [(Original Value - New Value) / Original Value] * 100
Conclusion: Mastering Percentages – A Stepping Stone to Success
While finding 100% of 40 is a simple calculation, the understanding of percentages goes far beyond this basic example. Mastering percentage calculations is essential for success in various academic and professional fields. By understanding the different methods for calculating percentages, their applications in real-world scenarios, and the underlying principles of fractions and ratios, you build a solid foundation for more advanced mathematical concepts and problem-solving abilities. Remember that practice is key. The more you work with percentages, the more intuitive and easy they will become. So, continue exploring, experimenting, and applying your knowledge to various situations to truly master this crucial mathematical skill.
Latest Posts
Latest Posts
-
90 Days From May 15
Sep 11, 2025
-
Gpm To Liters Per Minute
Sep 11, 2025
-
How Much Is 8 Ml
Sep 11, 2025
-
Convert Lb Hr To Gpm
Sep 11, 2025
-
How To Figure Slugging Percentage
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about What Is 100 Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.