What Is 15 Of 100.00
wordexpert
Sep 11, 2025 · 5 min read
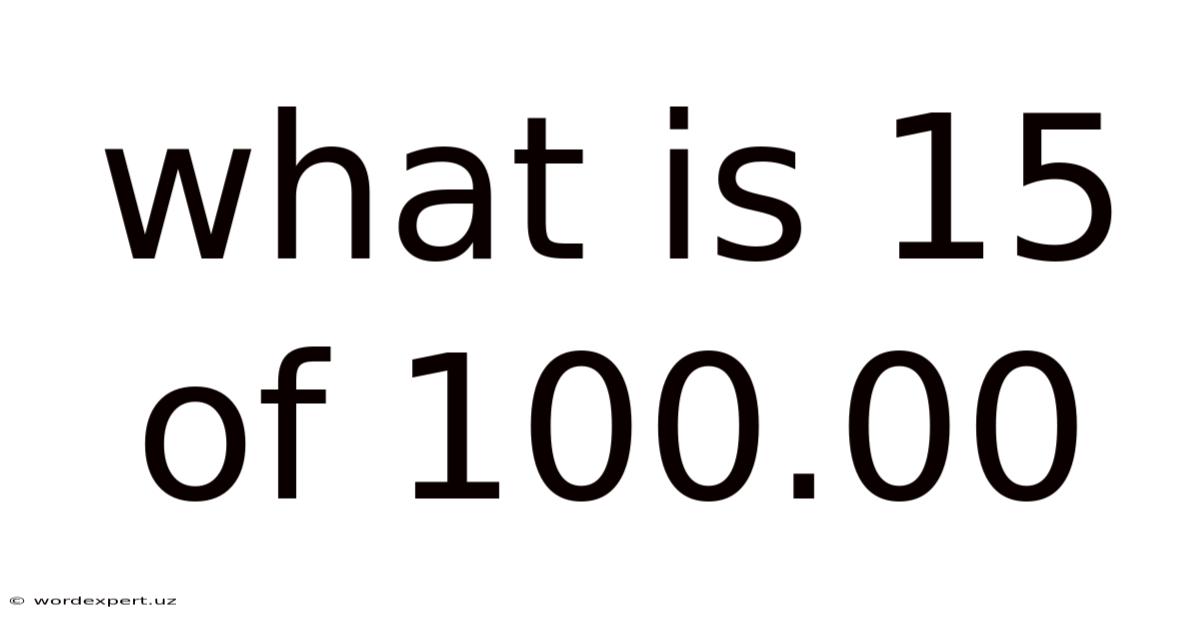
Table of Contents
What is 15% of 100.00? A Deep Dive into Percentages and Their Applications
Understanding percentages is a fundamental skill in everyday life, from calculating discounts and taxes to comprehending financial reports and statistical data. This article will thoroughly explore the question, "What is 15% of 100.00?", and will delve much deeper into the underlying concepts, providing a solid foundation for anyone looking to improve their understanding of percentages and their practical applications. We’ll cover multiple methods for calculating percentages, explore real-world examples, and address frequently asked questions.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ("per centum" in Latin). Therefore, 15% means 15 out of 100, or 15/100. This fractional representation is key to understanding how to calculate percentages.
Calculating 15% of 100.00: Three Methods
There are several ways to calculate 15% of 100.00. Let's explore three common approaches:
Method 1: Using the Fraction Method
As mentioned earlier, 15% can be expressed as the fraction 15/100. To find 15% of 100.00, we simply multiply 100.00 by the fraction:
100.00 * (15/100) = 15.00
This method is straightforward and clearly illustrates the fundamental concept of percentages.
Method 2: Using Decimal Conversion
Percentages can also be easily converted to decimals. To convert a percentage to a decimal, simply divide the percentage by 100. In this case, 15% becomes 0.15 (15 ÷ 100 = 0.15). Then, multiply the decimal by the original number:
100.00 * 0.15 = 15.00
This method is often preferred for its efficiency, especially when dealing with larger numbers or more complex calculations.
Method 3: Using a Calculator (or Spreadsheet Software)
Most calculators and spreadsheet programs have a percentage function. Simply enter "100.00 * 15%", and the calculator will automatically perform the calculation, giving you the answer: 15.00. This is the most convenient method for quick calculations, though understanding the underlying methods is crucial for problem-solving and error-checking.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is vital in numerous real-world scenarios. Here are a few examples:
-
Sales and Discounts: Imagine a store offering a 15% discount on a $100.00 item. Using our calculation, we know the discount is $15.00, making the final price $85.00.
-
Taxes: Sales tax is another common application. If the sales tax rate is 15%, the tax on a $100.00 item would be $15.00.
-
Tips and Gratuities: Calculating tips in restaurants often involves percentages. A 15% tip on a $100.00 bill would be $15.00.
-
Financial Investments: Understanding percentage changes in investments is crucial for tracking performance. If your investment grows by 15%, you can easily calculate the increase in value using percentage calculations.
-
Statistics and Data Analysis: Percentages are fundamental in presenting and interpreting statistical data. For example, expressing survey results as percentages helps to easily understand the proportions of different responses.
Beyond 15% of 100.00: Calculating Percentages of Other Numbers
The methods described above can be applied to calculate percentages of any number. Let's look at a few examples:
-
Calculating 15% of 50.00: Using the decimal method, 50.00 * 0.15 = 7.50
-
Calculating 25% of 200.00: Using the fraction method, 200.00 * (25/100) = 50.00
-
Calculating 10% of 1500.00: Using the calculator method, 1500.00 * 10% = 150.00
These examples highlight the versatility and importance of understanding how to calculate percentages.
Understanding Percentage Increase and Decrease
While we’ve focused on finding a percentage of a number, it’s also crucial to understand how to calculate percentage increases and decreases.
Percentage Increase: This involves finding the percentage difference between an original value and a new, higher value. The formula is:
[(New Value - Original Value) / Original Value] * 100%
For example, if a product's price increases from $100.00 to $115.00, the percentage increase is:
[(115.00 - 100.00) / 100.00] * 100% = 15%
Percentage Decrease: This is calculated similarly, but for situations where the new value is lower than the original value. The formula is:
[(Original Value - New Value) / Original Value] * 100%
For example, if a product's price decreases from $100.00 to $85.00, the percentage decrease is:
[(100.00 - 85.00) / 100.00] * 100% = 15%
Solving More Complex Percentage Problems
While the examples above are relatively simple, percentage problems can become more complex. For instance, you might need to calculate multiple percentages sequentially or work with compound interest. However, the fundamental principles remain the same: convert percentages to decimals or fractions and use multiplication and division appropriately.
Frequently Asked Questions (FAQ)
Q: What if I need to calculate a percentage of a number that isn't a whole number?
A: The methods remain the same. Simply treat the decimal portion of the number as you would any other number. For example, to calculate 15% of 105.50, you would multiply 105.50 by 0.15.
Q: How do I calculate the percentage one number represents of another?
A: Divide the first number by the second number and multiply by 100%. For example, to find what percentage 15 is of 100, you would perform (15/100) * 100% = 15%.
Q: Are there any online tools or calculators that can help me with percentage calculations?
A: Yes, many online calculators and tools are available that can simplify percentage calculations. These tools can be particularly helpful for more complex problems.
Conclusion
Understanding percentages is a practical skill that enhances your ability to navigate everyday situations effectively. We’ve explored the question "What is 15% of 100.00?" and expanded upon the underlying concepts of percentage calculations, showcasing multiple methods and highlighting their practical applications in various contexts. By mastering these fundamental principles, you can confidently tackle percentage-related problems in your personal and professional life, making informed decisions based on numerical data. Remember to practice using different methods to solidify your understanding and boost your confidence in handling percentage calculations. The more you practice, the more comfortable and proficient you will become.
Latest Posts
Latest Posts
-
Index Of Qualitative Variation Calculator
Sep 12, 2025
-
Capitalization Rate Calculator Real Estate
Sep 12, 2025
-
20 Oz How Many Cups
Sep 12, 2025
-
Weight Of Aluminum Sheet Metal
Sep 12, 2025
-
66 Meses Sao Quantos Anos
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 100.00 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.