What Is 15 Of 150
wordexpert
Sep 24, 2025 · 5 min read
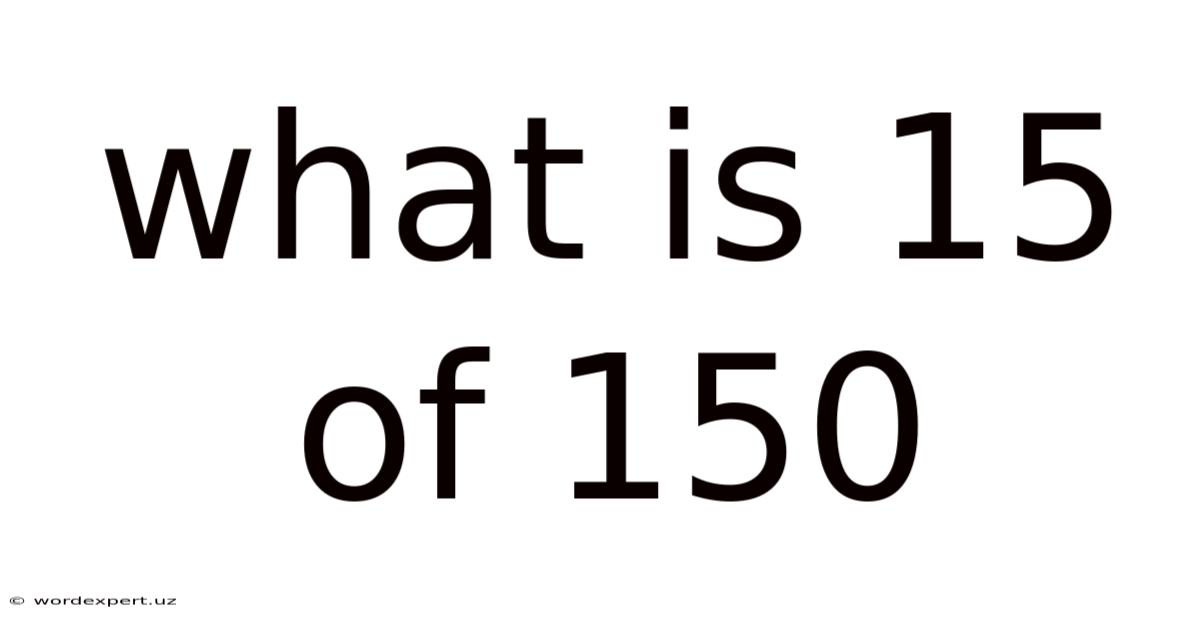
Table of Contents
What is 15 of 150? Understanding Percentages and Proportions
This article will delve into the seemingly simple question: "What is 15 of 150?" While the answer might seem immediately obvious to some, understanding this calculation opens the door to grasping fundamental concepts in mathematics, crucial for various applications in everyday life and professional fields. We'll explore different methods of solving this problem, including calculating percentages, ratios, and fractions, and discuss the broader implications of understanding proportions. This comprehensive guide will leave you confident in tackling similar problems and appreciating the underlying mathematical principles.
Understanding the Problem: Percentages, Fractions, and Ratios
The question "What is 15 of 150?" essentially asks us to determine what proportion or percentage 15 represents when compared to 150. This involves understanding the relationships between fractions, ratios, and percentages.
-
Fraction: A fraction represents a part of a whole. In this case, the fraction would be 15/150. This fraction can be simplified by finding the greatest common divisor (GCD) of 15 and 150, which is 15. Dividing both the numerator (15) and the denominator (150) by 15 simplifies the fraction to 1/10.
-
Ratio: A ratio expresses the relative size of two or more values. Here, the ratio is 15:150, which, when simplified, becomes 1:10. This means that for every 1 part, there are 10 parts in total.
-
Percentage: A percentage represents a fraction of 100. To find the percentage, we convert the fraction 1/10 to a percentage by multiplying by 100: (1/10) * 100 = 10%. Therefore, 15 is 10% of 150.
Method 1: Calculating the Percentage Directly
The most straightforward method to solve "What is 15 of 150?" is to calculate the percentage directly using the following formula:
(Part / Whole) * 100 = Percentage
In this case:
(15 / 150) * 100 = 10%
This calculation shows that 15 represents 10% of 150.
Method 2: Simplifying the Fraction
As mentioned earlier, simplifying the fraction 15/150 to its simplest form, 1/10, provides a clearer understanding of the relationship. This simplified fraction immediately reveals that 15 represents one-tenth of 150. Converting this fraction to a percentage (as shown above) gives us 10%.
Method 3: Using Proportions
Proportions are powerful tools for solving problems involving ratios. We can set up a proportion to solve for the unknown percentage:
15/150 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we can cross-multiply:
15 * 100 = 150 * x
1500 = 150x
x = 1500 / 150
x = 10
Therefore, x = 10%, confirming our previous calculations.
Real-World Applications: Why Understanding Proportions Matters
Understanding how to calculate proportions and percentages is vital in numerous real-world situations. Here are a few examples:
-
Finance: Calculating interest rates, discounts, tax amounts, and investment returns all rely on understanding percentages and proportions. For instance, determining the interest earned on a savings account or calculating the discount on a sale item requires these skills.
-
Science: Many scientific calculations, particularly in chemistry and physics, involve calculating proportions and concentrations. For example, determining the concentration of a solution or calculating the ratio of elements in a compound requires precise proportional calculations.
-
Business: Businesses use proportions to analyze sales data, track inventory, and manage budgets. Understanding market share, profit margins, and sales growth all rely on calculating proportions.
-
Everyday Life: We use proportions in everyday tasks such as cooking (adjusting recipes), measuring ingredients, and even dividing tasks amongst a group of people.
-
Data Analysis: In data analysis, proportions are used to understand the distribution of data and to draw meaningful conclusions. For example, determining the percentage of respondents who answered "yes" to a survey question involves calculating proportions.
Expanding the Concept: Working with Larger or Smaller Numbers
The principles discussed above apply equally to larger or smaller numbers. For example, let's consider finding what percentage 30 is of 300. Following the same method:
(30/300) * 100 = 10%
This again demonstrates that 30 represents 10% of 300. Similarly, calculating what percentage 1.5 is of 15 would also result in 10%. The key is understanding the underlying relationship between the parts and the whole.
Addressing Potential Challenges and Misconceptions
A common misconception when dealing with percentages is the mistaken belief that multiplying by the percentage directly will yield the correct answer. For instance, one might incorrectly think that 15% of 150 is 15 * 150 = 2250. This is wrong. Remember, the percentage is a fraction of the whole, requiring division before multiplication by 100.
Another challenge can arise when dealing with more complex scenarios involving multiple percentages or changes in proportions. These often require a step-by-step approach and a clear understanding of the order of operations.
Frequently Asked Questions (FAQ)
Q: What if the numbers aren't easily divisible?
A: If the numbers don't simplify easily, you can use a calculator to perform the division. The method remains the same: (Part/Whole) * 100.
Q: Can I use this method for any two numbers?
A: Yes, this method works for any two numbers where you want to find the percentage one number represents of the other. The larger number is always considered the whole.
Q: What if I need to find the whole number, given a percentage and a part?
A: In that case, you would rearrange the formula. If you know the percentage (P) and the part (Part), you can find the whole (Whole) using this formula: Whole = (Part / (P/100))
Conclusion: Mastering Proportions for a Brighter Future
Understanding "What is 15 of 150?" goes beyond a simple arithmetic calculation. It's about mastering the fundamentals of proportions, percentages, and fractions—skills crucial for academic success and navigating various aspects of daily life and professional endeavors. By grasping these concepts, you equip yourself with powerful tools for problem-solving, critical thinking, and making informed decisions across diverse fields. Remember that practice is key to mastering these concepts. The more you work with proportions and percentages, the more comfortable and confident you will become in applying them to a wide range of problems. So, continue practicing, and you'll find that these seemingly simple calculations unlock a world of opportunities.
Latest Posts
Latest Posts
-
20 000 Minutes To Days
Sep 25, 2025
-
30 Days From 11 17
Sep 25, 2025
-
2 Inch Circumference Ring Size
Sep 25, 2025
-
How Many Months Till 2026
Sep 25, 2025
-
Log Of A Negative Number
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 150 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.