What Is 18 / 20
wordexpert
Sep 18, 2025 · 5 min read
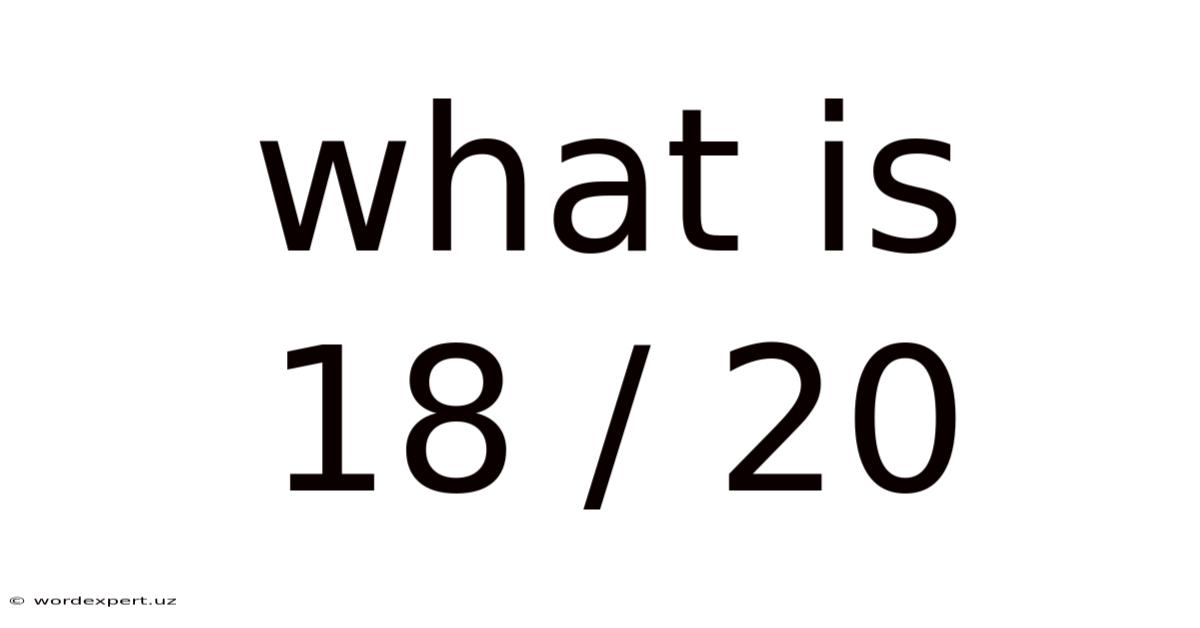
Table of Contents
What is 18/20? Understanding Fractions, Decimals, and Percentages
The seemingly simple question, "What is 18/20?", opens a door to a broader understanding of mathematical concepts crucial for everyday life. This article will explore not only the answer but also the underlying principles of fractions, decimals, and percentages, showing how they interrelate and how to confidently tackle similar problems. We'll delve into simplification, conversion methods, and practical applications, making this a comprehensive guide for learners of all levels.
Understanding Fractions: The Building Blocks
At its core, 18/20 is a fraction. A fraction represents a part of a whole. The top number, 18, is called the numerator, representing the number of parts we have. The bottom number, 20, is the denominator, representing the total number of parts the whole is divided into. So, 18/20 signifies 18 out of 20 equal parts.
Before diving into calculations, let's establish the importance of understanding fractions. They are fundamental in various fields, including:
- Cooking and Baking: Recipes often require fractional measurements (e.g., ½ cup of flour).
- Construction and Engineering: Precise measurements and calculations involving fractions are essential for building structures.
- Finance: Understanding fractions is key to comprehending interest rates, portions of investments, and financial ratios.
- Everyday Life: Sharing items equally, calculating discounts, or understanding proportions all involve fractions.
Simplifying Fractions: Finding the Lowest Terms
The fraction 18/20 can be simplified. Simplifying, or reducing a fraction to its lowest terms, means finding an equivalent fraction where the numerator and denominator have no common factors other than 1. This makes the fraction easier to understand and work with.
To simplify 18/20, we find the greatest common divisor (GCD) of 18 and 20. The GCD is the largest number that divides both 18 and 20 without leaving a remainder. In this case, the GCD is 2.
We divide both the numerator and the denominator by the GCD:
18 ÷ 2 = 9 20 ÷ 2 = 10
Therefore, the simplified fraction is 9/10. This means that 18/20 and 9/10 represent the same value. They are equivalent fractions.
Converting Fractions to Decimals: A Practical Approach
Fractions can be easily converted into decimals. To convert 9/10 (or 18/20) to a decimal, we simply divide the numerator by the denominator:
9 ÷ 10 = 0.9
Therefore, 18/20 is equal to 0.9 as a decimal. Decimals are particularly useful in calculations involving money, measurements, and scientific data.
Converting Fractions to Percentages: Expressing Parts as a Whole
Percentages express a fraction as a part of 100. To convert 9/10 to a percentage, we multiply the decimal equivalent (0.9) by 100:
0.9 × 100 = 90%
Therefore, 18/20 is equal to 90%. Percentages are widely used to represent proportions, rates of change, and probabilities. Understanding percentages is vital for interpreting statistics, analyzing data, and making informed decisions.
Illustrative Examples: Applying the Concepts
Let's illustrate the practical application of these concepts with a few examples:
Example 1: A student answered 18 out of 20 questions correctly on a test. What is their score as a percentage?
- Solution: The student's score is 18/20, which simplifies to 9/10 or 90%.
Example 2: A baker uses 18 grams of sugar out of a total of 20 grams required for a recipe. What fraction of the sugar has been used?
- Solution: The baker has used 18/20 of the sugar, which simplifies to 9/10.
Example 3: A shop offers a 10% discount on an item. If the original price is $20, what is the discount amount?
- Solution: The discount amount is 10% of $20, which is (10/100) × $20 = $2. This demonstrates the direct application of percentages to real-world scenarios.
Understanding the Relationship Between Fractions, Decimals, and Percentages
It's crucial to understand that fractions, decimals, and percentages are simply different ways of representing the same value. They are interchangeable, and the ability to convert between them is a valuable mathematical skill. The following table summarizes the equivalencies we've established:
| Fraction | Decimal | Percentage |
|---|---|---|
| 18/20 | 0.9 | 90% |
| 9/10 | 0.9 | 90% |
Beyond the Basics: Working with More Complex Fractions
While 18/20 is a relatively straightforward fraction, the principles discussed here apply to more complex fractions as well. The process of simplification, conversion to decimals and percentages remains the same, regardless of the complexity of the fraction. Remember to always simplify the fraction to its lowest terms before performing other calculations.
Frequently Asked Questions (FAQ)
Q1: How do I simplify fractions with larger numbers?
A1: Find the greatest common divisor (GCD) of the numerator and denominator. You can use methods like prime factorization or the Euclidean algorithm to find the GCD, especially for larger numbers. Then divide both the numerator and the denominator by the GCD.
Q2: What if the fraction has a remainder after division?
A2: If the division results in a remainder, you can express the remainder as a fraction. For example, 19/5 = 3 with a remainder of 4, which can be written as 3 4/5 (a mixed number). Alternatively, you can express it as a decimal with a repeating or terminating decimal part.
Q3: Are there any online tools to help simplify fractions?
A3: Many online calculators and websites are available to help simplify fractions, convert between fractions, decimals, and percentages, and perform other mathematical operations.
Q4: Why is simplifying fractions important?
A4: Simplifying fractions makes them easier to understand and work with. It reduces the complexity of calculations and helps in visualizing the proportion represented by the fraction.
Conclusion: Mastering the Fundamentals
The seemingly simple question, "What is 18/20?", has led us on a journey through the fundamentals of fractions, decimals, and percentages. We've seen how these concepts are interconnected and how they find applications in various aspects of life. Mastering these concepts builds a strong foundation for more advanced mathematical studies and empowers you to confidently tackle real-world problems involving proportions, ratios, and calculations. Remember, understanding the underlying principles is as crucial as knowing the answer itself. Practice regularly, explore different methods, and don't hesitate to seek further learning opportunities to solidify your understanding of these fundamental mathematical concepts.
Latest Posts
Latest Posts
-
75 Sq Meters In Feet
Sep 18, 2025
-
1 8 Inches On A Ruler
Sep 18, 2025
-
Converting Rectangular Points To Polar
Sep 18, 2025
-
Halfway Point Between Two Places
Sep 18, 2025
-
600 000 Milliseconds To Minutes
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What Is 18 / 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.