What Is 2.5 Of 943
wordexpert
Sep 11, 2025 · 5 min read
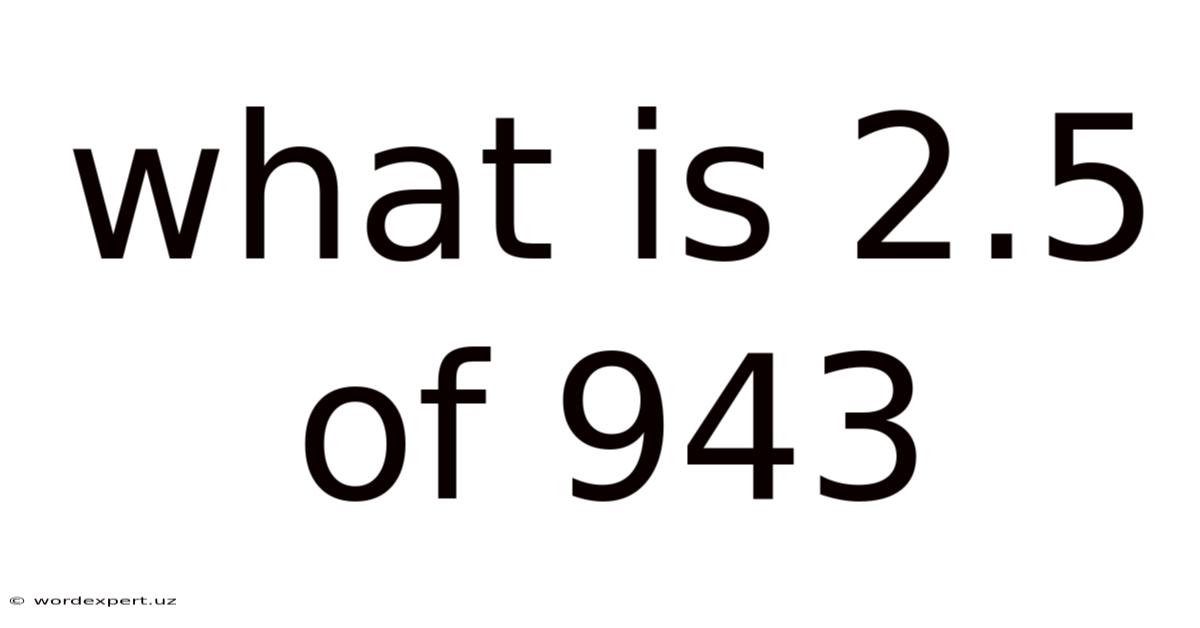
Table of Contents
What is 2.5% of 943? A Deep Dive into Percentages and Their Applications
Finding 2.5% of 943 might seem like a simple arithmetic problem, but understanding the underlying concepts of percentages and their practical applications opens up a world of possibilities. This article will not only show you how to calculate 2.5% of 943 but also explore the broader context of percentages, including their uses in various fields and some common misconceptions. We'll delve into the mechanics of the calculation, provide alternative methods, and address frequently asked questions, making this a comprehensive guide for anyone wanting to master percentage calculations.
Introduction: Understanding Percentages
A percentage is simply a fraction expressed as a part of 100. The term "percent" comes from the Latin "per centum," meaning "out of one hundred." When we say 2.5% of 943, we're asking what amount represents 2.5 parts out of every 100 parts of 943. Understanding this fundamental concept is crucial for tackling percentage problems effectively. Percentages are ubiquitous in everyday life, from calculating sales tax and discounts to understanding financial reports and statistical data.
Method 1: The Direct Calculation Method
The most straightforward method to calculate 2.5% of 943 involves converting the percentage to a decimal and then multiplying it by the number.
-
Step 1: Convert the percentage to a decimal: To convert 2.5% to a decimal, we divide it by 100: 2.5% / 100 = 0.025
-
Step 2: Multiply the decimal by the number: Now, we multiply the decimal (0.025) by 943: 0.025 * 943 = 23.575
Therefore, 2.5% of 943 is 23.575.
Method 2: Using Fractions
Percentages can also be represented as fractions. 2.5% can be written as 2.5/100, which simplifies to 1/40. This fractional representation offers an alternative approach to the calculation.
-
Step 1: Express the percentage as a fraction: 2.5% = 2.5/100 = 1/40
-
Step 2: Multiply the fraction by the number: (1/40) * 943 = 943/40
-
Step 3: Perform the division: 943/40 = 23.575
This method confirms our earlier result: 2.5% of 943 is 23.575.
Method 3: Breaking Down the Calculation
For a deeper understanding, we can break down the calculation into smaller, more manageable steps. Since 2.5% is half of 5%, we can first calculate 5% of 943 and then halve the result.
-
Step 1: Calculate 1% of 943: 943 / 100 = 9.43
-
Step 2: Calculate 5% of 943: 9.43 * 5 = 47.15
-
Step 3: Calculate 2.5% of 943: 47.15 / 2 = 23.575
This approach demonstrates the flexibility of percentage calculations and helps visualize the relationship between different percentages.
Applications of Percentage Calculations
The ability to calculate percentages is a fundamental skill with widespread applications across numerous fields:
-
Finance: Calculating interest rates, loan repayments, returns on investments, and analyzing financial statements all rely heavily on percentage calculations. Understanding percentage changes in stock prices or interest rates is vital for informed investment decisions.
-
Retail: Discounts, sales tax, profit margins, and markup percentages are all core concepts in retail. Calculating the final price after a discount or determining the profit margin on a product requires proficiency in percentage calculations.
-
Science: Percentages are used extensively in scientific research to represent proportions, error margins, and statistical significance. For example, expressing the concentration of a solution or the success rate of an experiment often involves percentages.
-
Everyday Life: Calculating tips in restaurants, understanding tax rates, interpreting survey results, and comparing prices all involve percentages. These daily applications make mastering percentage calculations a valuable life skill.
-
Data Analysis: In data analysis, percentages are used to represent proportions within datasets, making it easier to understand and visualize trends and patterns. For instance, expressing the percentage of respondents who answered "yes" to a survey question provides a clear and concise summary of the data.
Common Misconceptions about Percentages
Several misconceptions surrounding percentages can lead to incorrect calculations or misinterpretations of data:
-
Confusing percentage change with percentage points: A change from 10% to 15% is a 5 percentage point increase, but a 50% increase relative to the original 10%. The difference is crucial for accurate analysis.
-
Incorrectly applying percentage increases and decreases consecutively: A 10% increase followed by a 10% decrease does not result in the original value. This is because the second percentage is applied to a new, larger base.
-
Misinterpreting percentages in context: A percentage alone lacks meaning without the context of the base value. Saying "sales increased by 20%" is meaningless without knowing the original sales figure.
Frequently Asked Questions (FAQ)
-
Q: How can I calculate a percentage increase or decrease?
A: To calculate a percentage increase, subtract the original value from the new value, divide the result by the original value, and multiply by 100. For a percentage decrease, follow the same steps but use the absolute difference between the new and original values.
-
Q: How do I calculate the percentage of a specific value within a larger total?
A: Divide the specific value by the larger total, and then multiply by 100.
-
Q: What are some useful tools or calculators for working with percentages?
A: Many online calculators and spreadsheet software (like Microsoft Excel or Google Sheets) provide built-in functions for percentage calculations, simplifying complex computations.
-
Q: Why is it important to understand percentages?
A: Understanding percentages is essential for making informed decisions in various aspects of life, from personal finance to professional settings. It enables accurate interpretation of data and facilitates critical thinking skills.
Conclusion: Mastering the Art of Percentage Calculations
Calculating 2.5% of 943, as we've demonstrated, is a straightforward process once the underlying principles of percentages are understood. This seemingly simple calculation opens a door to a vast landscape of applications in numerous fields. By mastering the techniques outlined in this article and avoiding common misconceptions, you'll not only be able to solve percentage problems accurately but also gain a valuable skill that enhances your analytical and problem-solving abilities. The ability to work confidently with percentages empowers you to navigate the complexities of the world around you with greater understanding and clarity. Remember to practice regularly, exploring different methods and applications to solidify your grasp of this crucial mathematical concept.
Latest Posts
Latest Posts
-
1 Kg Water To Liters
Sep 12, 2025
-
64 Fl Oz To Ml
Sep 12, 2025
-
34 26 36 Body Shape
Sep 12, 2025
-
How Old Is My Tree
Sep 12, 2025
-
Index Of Qualitative Variation Calculator
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 2.5 Of 943 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.