What Is 20 Of 1
wordexpert
Sep 18, 2025 · 5 min read
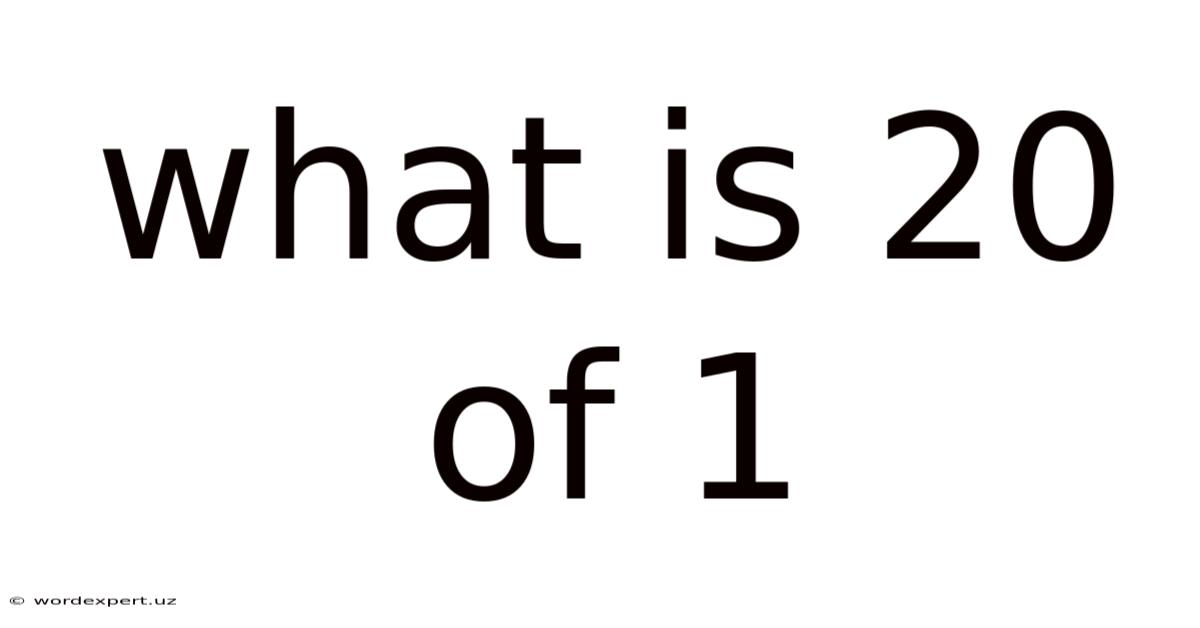
Table of Contents
What is 20 of 1? Deconstructing Fractions, Percentages, and Ratios
The seemingly simple question, "What is 20 of 1?" might initially appear trivial. However, it opens a door to a deeper understanding of fundamental mathematical concepts like fractions, percentages, and ratios. This article will explore various interpretations of this question, providing a comprehensive explanation suitable for learners of all levels, from elementary school students to those refreshing their mathematical foundations. We'll delve into the practical applications of these concepts and address common misconceptions.
Understanding the Question: Different Interpretations
The phrasing "20 of 1" is ambiguous. It doesn't explicitly state the operation intended. To find a meaningful answer, we need to interpret it within the context of mathematical operations. This ambiguity allows us to explore several crucial mathematical concepts:
-
Fractions: "20 of 1" can be interpreted as the fraction 20/1. This represents 20 parts out of a total of 1 part. This fraction is an improper fraction because the numerator (20) is larger than the denominator (1).
-
Percentages: While not directly implied, we could consider "20 of 1" as representing 20% of 1. This involves converting the fraction 20/1 into a percentage.
-
Ratios: We can interpret it as a ratio of 20:1, comparing the quantity 20 to the quantity 1. This ratio indicates a proportional relationship between two values.
Fractional Interpretation: 20/1
The most straightforward interpretation of "20 of 1" is as the fraction 20/1. This fraction represents a whole number, specifically 20. Let's examine why:
A fraction, in its simplest form, represents a part of a whole. The numerator (top number) indicates the number of parts we have, and the denominator (bottom number) indicates the total number of parts that make up the whole.
In the fraction 20/1, the numerator is 20, indicating that we have 20 parts. The denominator is 1, signifying that the whole consists of only one part. Therefore, having 20 parts of a single-part whole means we have 20 wholes.
Example: Imagine you have a single pizza (the whole, represented by 1). If you magically increase the amount of pizza to 20 times the original size, you have 20 pizzas. This scenario directly corresponds to the fraction 20/1.
Percentage Interpretation: 20% of 1
While not directly implied, we can interpret "20 of 1" in the context of percentages. To do this, we first need to convert the fraction 20/1 into a percentage.
The process involves converting the fraction to a decimal and then multiplying by 100%:
-
Convert the fraction to a decimal: 20/1 = 20.0
-
Multiply by 100%: 20.0 * 100% = 2000%
This means that 20 of 1 is equivalent to 2000% of 1. This might seem counterintuitive, but it highlights the fact that percentages can represent values greater than 100%. Having 2000% of something means you have 20 times the original amount.
Example: If you start with $1 and increase it by 2000%, you will have $21 ($1 + $20). This again aligns with the concept of having 20 times the original amount.
Ratio Interpretation: 20:1
The expression "20 of 1" can also be viewed as a ratio of 20:1. Ratios show the proportional relationship between two quantities. In this case, the ratio indicates that there are 20 units of one quantity for every 1 unit of another.
Examples:
- Recipe: A recipe might call for a 20:1 ratio of sugar to salt. This means for every 1 gram of salt, you would use 20 grams of sugar.
- Scale Model: A scale model of a building might have a scale of 20:1. This means that 20 units on the model represent 1 unit in reality.
Extending the Concept: Working with Different Denominators
While "20 of 1" provides a clear understanding of improper fractions, let's explore what happens when we change the denominator. Consider "20 of 5":
This translates to the fraction 20/5. Simplifying this fraction, we get: 20/5 = 4.
This illustrates the general principle: the result depends on the relationship between the numerator and the denominator. The numerator represents the quantity, while the denominator represents the size of the whole or the number of parts that make up the whole.
Practical Applications
Understanding these concepts – fractions, percentages, and ratios – has wide-ranging practical applications in daily life:
- Cooking: Following recipes often involves working with ratios of ingredients.
- Finance: Calculating percentages for interest, discounts, or taxes is crucial in financial planning.
- Construction: Blueprints and scale models utilize ratios to represent real-world dimensions.
- Data Analysis: Percentages and ratios are essential tools for interpreting data and making informed decisions.
Frequently Asked Questions (FAQ)
Q1: Can a fraction have a denominator of 0?
A1: No, a fraction cannot have a denominator of 0. Division by zero is undefined in mathematics.
Q2: How do I convert a fraction to a decimal?
A2: To convert a fraction to a decimal, simply divide the numerator by the denominator.
Q3: How do I convert a decimal to a percentage?
A3: To convert a decimal to a percentage, multiply the decimal by 100% and add the percent symbol.
Q4: What are some other ways to represent "20 of 1"?
A4: Besides fraction, percentage, and ratio, you could also represent it verbally as "twenty times one" or "twenty multiplied by one."
Q5: What if the number "20" were replaced with a variable, say 'x'?
A5: If we replaced 20 with 'x', the expression becomes "x of 1," which would simply be represented as the fraction x/1, or simply x. This highlights that the concept extends beyond the specific number 20.
Conclusion: Beyond the Surface
The question "What is 20 of 1?" serves as a springboard for exploring fundamental mathematical concepts. While seemingly simple at first glance, it reveals the intricacies of fractions, percentages, and ratios. Understanding these concepts is not just about solving equations; it's about gaining a deeper appreciation for how mathematics underlies many aspects of our daily lives. By grasping these core ideas, we develop crucial problem-solving skills and a more robust understanding of the numerical world around us. The seemingly simple can often unlock profound insights, and this exploration demonstrates just that. Remember, mathematics is not merely a collection of rules; it’s a powerful tool for understanding and interacting with the world.
Latest Posts
Latest Posts
-
How Long Is 56 Hours
Sep 19, 2025
-
What Is 20 Of 32
Sep 19, 2025
-
How Long Is 5 Years
Sep 19, 2025
-
Convertidor De Decimal A Fraccion
Sep 19, 2025
-
Best Uv Index To Tan
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.