What Is 3 Of 1200
wordexpert
Sep 15, 2025 · 5 min read
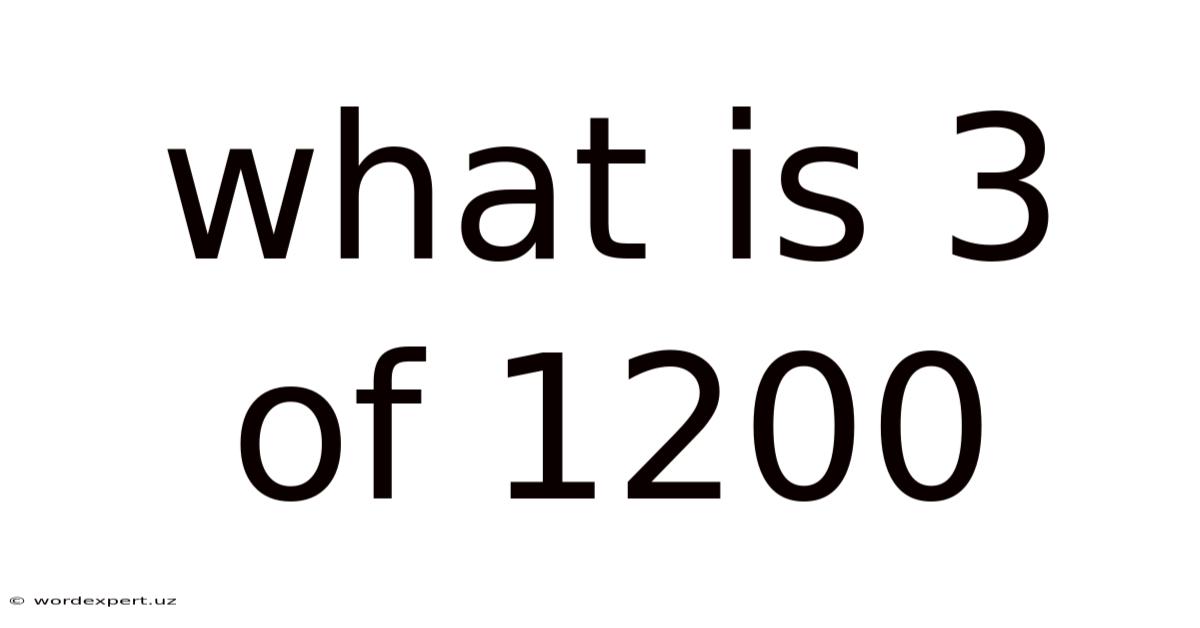
Table of Contents
What is 3/1200? Understanding Fractions and Their Applications
This article delves into the seemingly simple question: "What is 3/1200?" While the answer might appear straightforward, exploring this fraction provides a valuable opportunity to understand fundamental concepts in mathematics, particularly fractions, their simplification, decimal equivalents, and their practical applications in various fields. We'll move beyond simply calculating the result to explore the underlying principles and demonstrate how this type of calculation is used in real-world scenarios.
Understanding Fractions: A Quick Refresher
Before diving into 3/1200, let's briefly review the concept of fractions. A fraction represents a part of a whole. It consists of two parts:
- Numerator: The top number (in this case, 3) represents the number of parts we have.
- Denominator: The bottom number (in this case, 1200) represents the total number of equal parts the whole is divided into.
Therefore, 3/1200 signifies 3 out of 1200 equal parts.
Calculating 3/1200: Simplification and Decimal Equivalents
The simplest way to understand 3/1200 is to simplify the fraction. Simplification involves dividing both the numerator and the denominator by their greatest common divisor (GCD). In this case, the GCD of 3 and 1200 is 3. Dividing both the numerator and the denominator by 3, we get:
3 ÷ 3 = 1 1200 ÷ 3 = 400
Therefore, 3/1200 simplifies to 1/400.
This simplified fraction is easier to work with. To express this as a decimal, we divide the numerator (1) by the denominator (400):
1 ÷ 400 = 0.0025
So, 3/1200 is equivalent to 1/400, which is equal to 0.0025.
Practical Applications of Fractions Like 3/1200
Fractions, even seemingly small ones like 1/400, find practical application across numerous fields. Here are some examples:
1. Percentage Calculations: Converting 1/400 to a percentage involves multiplying by 100:
(1/400) * 100 = 0.25%
This means 3/1200 represents 0.25% of the whole. This is useful in scenarios involving proportions, such as calculating the percentage of defective items in a batch of 1200 products, where only 3 are faulty.
2. Financial Calculations: Fractions are crucial in finance. For instance, consider a scenario where you invest a certain amount, and your return is 3 out of every 1200 invested. Calculating the return on investment (ROI) would involve using the fraction 3/1200.
3. Engineering and Precision Measurement: In engineering and precision manufacturing, fractions are frequently used. Imagine a scenario where a tiny component needs to be precisely 3 millimeters out of a total length of 1200 millimeters. The fraction 3/1200 would represent the component's proportion in the overall design.
4. Scientific Research: Scientific research heavily utilizes fractions and percentages. Experiments may involve ratios and proportions represented using fractions. For example, a study might involve analyzing the success rate of a treatment, where 3 out of 1200 participants showed positive results.
5. Statistical Analysis: Statistics relies extensively on fractions and their decimal equivalents. Sample sizes, probabilities, and proportions are often expressed as fractions.
Expanding on the Concept: Proportions and Ratios
Understanding 3/1200 also allows us to explore the concepts of proportions and ratios. A proportion is a statement that two ratios are equal. A ratio is a comparison of two quantities.
In the case of 3/1200, we can express this as a ratio: 3:1200. This means that for every 3 units, there are 1200 total units. We can set up a proportion to find the equivalent value for a different number of units.
For instance, if we wanted to find out what proportion 6 units would represent out of a total of 2400 units, we could set up the following proportion:
3/1200 = x/2400
Solving for x, we find that x = 6. This illustrates how understanding the fraction 3/1200 can help solve similar proportional problems.
Beyond the Basics: Working with More Complex Fractions
While 3/1200 is a relatively simple fraction, the principles involved can be applied to more complex scenarios. Let's consider an example:
What is 27/3600?
First, simplify the fraction. The GCD of 27 and 3600 is 27:
27 ÷ 27 = 1 3600 ÷ 27 = 133.333... (approximately)
So, 27/3600 simplifies to approximately 1/133.33. Converting this to a decimal:
1 ÷ 133.33 ≈ 0.0075
This demonstrates how the fundamental principles learned from simplifying 3/1200 apply to more complex fractions.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of 3/1200?
A: The simplest form of 3/1200 is 1/400.
Q: What is 3/1200 as a decimal?
A: 3/1200 is equal to 0.0025.
Q: How do I convert 3/1200 to a percentage?
A: Convert the fraction to a decimal (0.0025) and multiply by 100 to get 0.25%.
Q: Are there any real-world examples of using fractions like 3/1200?
A: Yes, many fields, including finance, engineering, science, and statistics, use such fractions for calculations involving proportions, ratios, percentages, and probabilities.
Q: Can I use a calculator to solve 3/1200?
A: Yes, simply divide 3 by 1200 using a calculator.
Conclusion
The seemingly simple question of "What is 3/1200?" provides a rich learning opportunity. Understanding this fraction requires grasping the fundamentals of fractions, simplification techniques, decimal conversion, and the connection to concepts like percentages, ratios, and proportions. These concepts are not just theoretical; they are essential tools used daily in various professions and fields. By understanding the principles behind this simple fraction, we've opened the door to a wider understanding of mathematical concepts and their real-world implications. This exploration should empower you to tackle more complex fractional calculations with confidence and apply this knowledge to diverse problem-solving scenarios.
Latest Posts
Latest Posts
-
How Long Is 77 Weeks
Sep 15, 2025
-
Cuantos Dias Son 120 Horas
Sep 15, 2025
-
Military Time In Minutes Chart
Sep 15, 2025
-
22 Por Ciento De 100
Sep 15, 2025
-
37 5 Out Of 50 Grade
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 3 Of 1200 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.