What Is 30 Of 16
wordexpert
Sep 25, 2025 · 5 min read
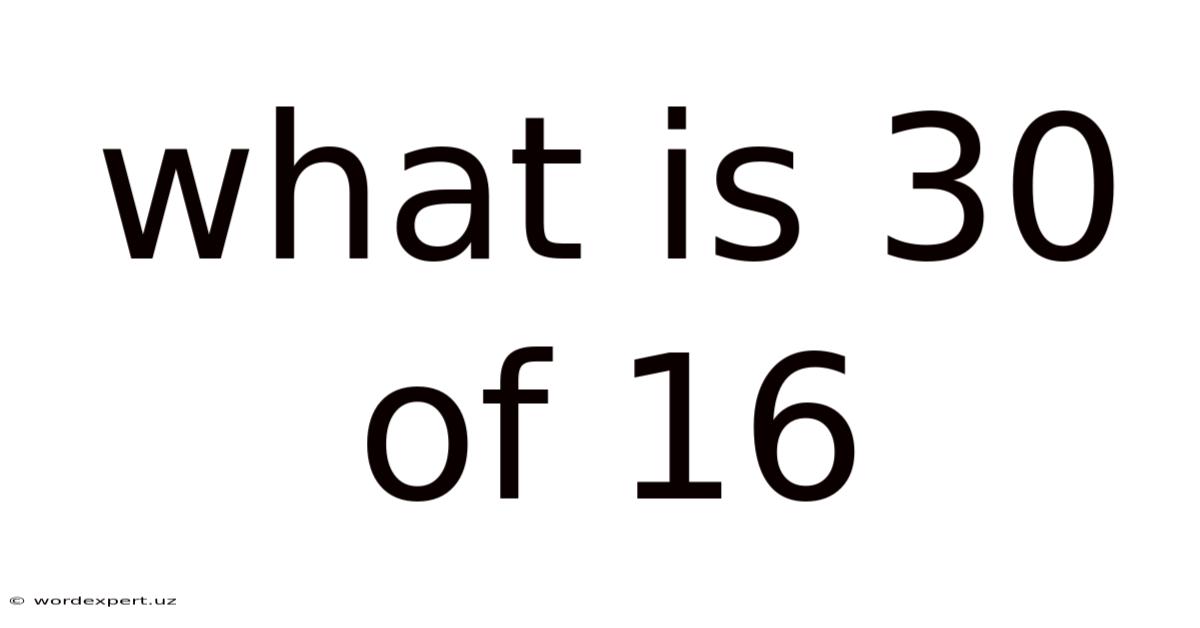
Table of Contents
What is 30% of 16? Understanding Percentages and Their Applications
Finding 30% of 16 might seem like a simple calculation, but understanding the underlying principles of percentages is crucial for a wide range of applications, from everyday budgeting and shopping to complex financial analyses and scientific calculations. This article will not only show you how to calculate 30% of 16 but will also delve into the broader concept of percentages, exploring different calculation methods and highlighting their practical uses.
Introduction: Deconstructing Percentages
A percentage is simply a fraction expressed as a part of 100. The term "percent" comes from the Latin "per centum," meaning "out of a hundred." Therefore, 30% means 30 out of 100, or 30/100, which can be simplified to 3/10. This understanding forms the foundation for calculating any percentage of a given number.
Method 1: Converting Percentage to Decimal
The most common method for calculating a percentage of a number involves converting the percentage to a decimal. To do this, we divide the percentage by 100.
-
Step 1: Convert 30% to a decimal: 30 ÷ 100 = 0.30
-
Step 2: Multiply the decimal by the number: 0.30 × 16 = 4.8
Therefore, 30% of 16 is 4.8.
This method is straightforward and easily adaptable to any percentage calculation. For instance, to find 75% of 20, you would convert 75% to 0.75 and multiply it by 20 (0.75 × 20 = 15).
Method 2: Using Fractions
As mentioned earlier, percentages can be expressed as fractions. This method offers a different perspective and can be particularly useful for understanding the underlying relationship between the percentage and the whole.
-
Step 1: Express 30% as a fraction: 30/100
-
Step 2: Simplify the fraction (if possible): 30/100 simplifies to 3/10
-
Step 3: Multiply the fraction by the number: (3/10) × 16 = 48/10
-
Step 4: Convert the improper fraction to a decimal: 48/10 = 4.8
This method provides a deeper understanding of the proportional relationship. It shows that 30% of 16 represents 3 out of every 10 parts of 16.
Method 3: Using Proportions
This method is particularly helpful for solving more complex percentage problems. It uses the concept of ratios and proportions to find the unknown value.
-
Step 1: Set up a proportion: 30/100 = x/16 (where 'x' represents the unknown value, which is 30% of 16)
-
Step 2: Cross-multiply: 30 × 16 = 100 × x
-
Step 3: Solve for x: 480 = 100x => x = 480/100 = 4.8
Again, we arrive at the same answer: 30% of 16 is 4.8. This method is particularly useful when dealing with problems where you need to find the percentage or the whole number, given other parts of the equation.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world scenarios. Here are a few examples:
-
Sales and Discounts: Calculating discounts on sale items. If a shirt costs $20 and is on sale for 20% off, you would calculate 20% of $20 to find the discount amount.
-
Taxes: Calculating sales tax or income tax. Sales tax is usually a percentage of the purchase price.
-
Tips and Gratuities: Calculating tips in restaurants or service charges. A 15% tip on a $50 bill requires a percentage calculation.
-
Interest Rates: Understanding interest rates on loans, savings accounts, or investments. Interest is often calculated as a percentage of the principal amount.
-
Financial Analysis: Calculating profit margins, return on investment (ROI), and other key financial metrics. These calculations rely heavily on percentages.
-
Scientific Applications: Many scientific fields use percentages to represent data, such as expressing the concentration of a solution or the percentage of a population with a specific trait.
Common Mistakes to Avoid
While percentage calculations are relatively simple, several common mistakes can lead to inaccurate results:
-
Incorrect Decimal Conversion: Failing to correctly convert the percentage to a decimal is a frequent error. Always remember to divide the percentage by 100.
-
Mixing Up the Order of Operations: Ensure you follow the correct order of operations (multiplication before addition or subtraction).
-
Improper Rounding: Round off your answer to the appropriate number of decimal places, depending on the context of the problem.
-
Using the Wrong Formula: When solving more complex percentage problems, choose the appropriate formula or method.
Frequently Asked Questions (FAQs)
-
Q: How do I calculate a percentage increase or decrease?
A: To calculate a percentage increase, find the difference between the new value and the original value, then divide by the original value and multiply by 100. A percentage decrease is calculated similarly, but the difference is negative.
-
Q: What if I need to find the original number, given a percentage and the resulting value?
A: This involves working backward. If you know that a certain percentage of a number is 'x', you can set up a proportion or equation to solve for the original number. For example, if 25% of a number is 10, you can set up the equation: 0.25 * y = 10, and solve for 'y'.
-
Q: Are there any online calculators or tools to help with percentage calculations?
A: While this article focuses on manual calculation methods, many online calculators and spreadsheet programs can perform percentage calculations automatically. These tools can be helpful for double-checking your work or for complex calculations.
Conclusion: Mastering Percentages for a Brighter Future
Understanding percentages is a fundamental skill applicable to numerous aspects of life. From personal finance to professional fields, the ability to accurately calculate and interpret percentages empowers informed decision-making. By mastering the methods outlined in this article, you'll not only be able to confidently solve problems like "What is 30% of 16?" but also navigate a wide range of scenarios requiring percentage calculations. Remember to practice regularly and apply these concepts in real-world situations to reinforce your understanding and build confidence in your mathematical abilities. The seemingly simple calculation of 30% of 16 opens a door to a much broader understanding of the power and versatility of percentages.
Latest Posts
Latest Posts
-
88 Days Ago From Today
Sep 25, 2025
-
2 000 Miles To Km
Sep 25, 2025
-
El 10 Porciento De 1000
Sep 25, 2025
-
Weight Of 1 4 Glass
Sep 25, 2025
-
Calculate Labour Force Participation Rate
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.