What Is 30 Of 24
wordexpert
Sep 21, 2025 · 5 min read
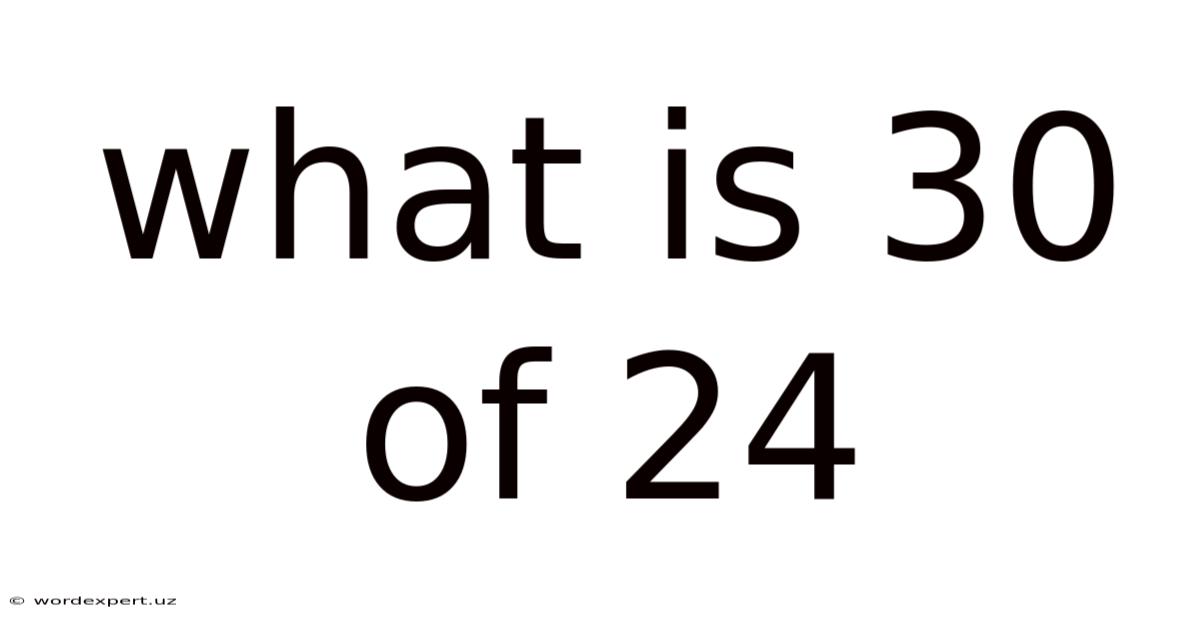
Table of Contents
What is 30% of 24? A Deep Dive into Percentages and Their Applications
Finding 30% of 24 might seem like a simple arithmetic problem, but it opens the door to understanding a fundamental concept in mathematics and its widespread applications in everyday life. This article will not only provide the solution but will also explore the underlying principles of percentages, different methods for calculating them, and real-world examples showcasing their importance.
Introduction: Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred" (per centum in Latin). Percentages are used to represent proportions, rates, or changes, making them a crucial tool for comparing and analyzing data across various fields. Understanding percentages is essential in areas like finance, statistics, science, and even everyday shopping. The question "What is 30% of 24?" is essentially asking for 30 parts out of 100 parts of 24.
Method 1: Converting Percentage to Decimal
The most straightforward method involves converting the percentage to a decimal and then multiplying it by the given number.
-
Step 1: Convert the percentage to a decimal. To convert 30% to a decimal, divide it by 100: 30% ÷ 100 = 0.30 or simply 0.3
-
Step 2: Multiply the decimal by the number. Multiply 0.3 by 24: 0.3 x 24 = 7.2
Therefore, 30% of 24 is 7.2.
Method 2: Using Fractions
Percentages can also be expressed as fractions. This method provides a different perspective and can be helpful in understanding the underlying relationship between fractions and percentages.
-
Step 1: Express the percentage as a fraction. 30% can be written as 30/100.
-
Step 2: Simplify the fraction (if possible). The fraction 30/100 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 10: 30/100 = 3/10
-
Step 3: Multiply the fraction by the number. Multiply 3/10 by 24: (3/10) x 24 = 72/10
-
Step 4: Convert the improper fraction to a decimal. 72/10 = 7.2
Again, we arrive at the answer: 30% of 24 is 7.2.
Method 3: Proportion Method
This method uses the concept of proportions to solve the problem. It's particularly helpful for visualizing the relationship between the percentage, the whole, and the part.
-
Step 1: Set up a proportion. We can set up a proportion as follows:
30/100 = x/24
Where 'x' represents the unknown value (30% of 24).
-
Step 2: Cross-multiply. Cross-multiplying gives us:
100x = 30 x 24
-
Step 3: Solve for x. This simplifies to:
100x = 720
x = 720/100
x = 7.2
Therefore, 30% of 24 is 7.2.
Method 4: Using a Calculator
Most calculators have a percentage function. Simply enter 24, press the multiplication key, then enter 30 and the percentage key (%). The calculator will automatically perform the calculation and display the answer: 7.2. This is the most efficient method for quick calculations, particularly for more complex percentage problems.
Explanation of the Result: What Does 7.2 Mean?
The result, 7.2, represents 30% of the total value 24. It indicates that if you divide 24 into 100 equal parts, 30 of those parts would add up to 7.2. This concept is fundamental to understanding proportions and ratios in many practical scenarios.
Real-World Applications of Percentages
Percentages are ubiquitous in everyday life, influencing numerous aspects of our daily decisions and understanding the world around us. Here are just a few examples:
-
Finance: Calculating interest rates on loans, savings accounts, and investments heavily relies on percentages. Understanding compound interest, which involves calculating interest on both the principal amount and accumulated interest, relies on percentage calculations. Also, analyzing financial statements, such as profit margins or expense ratios, requires using percentages.
-
Sales and Discounts: Retail stores frequently advertise discounts as percentages (e.g., "30% off"). Calculating the final price after a discount requires determining the percentage discount and subtracting it from the original price.
-
Taxes: Sales taxes, income taxes, and property taxes are all expressed as percentages of the assessed value or income. Calculating the final price after taxes involves adding the tax percentage to the original cost.
-
Statistics and Data Analysis: Percentages are crucial in presenting and interpreting statistical data. For instance, representing survey results, demographics, or performance metrics often involves percentages. Analyzing data to understand trends, relationships, and comparisons often necessitates the use of percentages.
-
Science and Engineering: Percentages are used extensively in scientific calculations and engineering design. For example, expressing concentrations of solutions, calculating efficiency of systems, or determining error margins in experiments all use percentages.
-
Everyday Life: Determining tips in restaurants, calculating grades in school, or understanding nutritional information on food labels frequently involves percentage calculations.
Frequently Asked Questions (FAQ)
-
Q: How can I calculate percentages mentally? A: For simple percentages like 10%, 20%, 50%, etc., it's relatively easy to do mental math. For example, 10% of a number is just that number divided by 10. 20% is double that. 50% is half the number. For more complex percentages, it's advisable to use the decimal or fraction methods described above.
-
Q: What if I need to find a percentage of a number that is not a whole number? A: The methods described above work perfectly well even if the number you're working with is a decimal or a fraction. Just apply the same steps.
-
Q: Can I use different methods to check my answers? A: Yes, absolutely! Using two different methods to solve the same problem is a great way to verify the accuracy of your answer.
-
Q: What are some common percentage calculation mistakes to avoid? A: Common mistakes include incorrect conversion of percentages to decimals, misplacing decimal points during multiplication, and not understanding the context of the problem (e.g., whether the problem requires adding or subtracting the percentage). Always double-check your work.
Conclusion: Mastering Percentages
Understanding percentages is a fundamental skill that extends far beyond simple arithmetic problems like "What is 30% of 24?". It's a cornerstone of numeracy, critical for success in various fields and for making informed decisions in everyday life. By mastering the different methods of calculating percentages and understanding their applications, you equip yourself with a powerful tool for navigating the quantitative aspects of the world. This article has aimed to provide not just a solution to a specific problem, but a comprehensive understanding of the concept of percentages and their relevance in our lives. Continue practicing and applying these methods to build your confidence and proficiency in working with percentages.
Latest Posts
Latest Posts
-
Punnett Square Eye Color Calculator
Sep 21, 2025
-
How To Calculate Engine Capacity
Sep 21, 2025
-
Acid Test Quick Ratio Calculator
Sep 21, 2025
-
How Do You Calculate Kda
Sep 21, 2025
-
10 Of 10 000 Dollars
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.