What Is 30 Of 35
wordexpert
Sep 14, 2025 · 5 min read
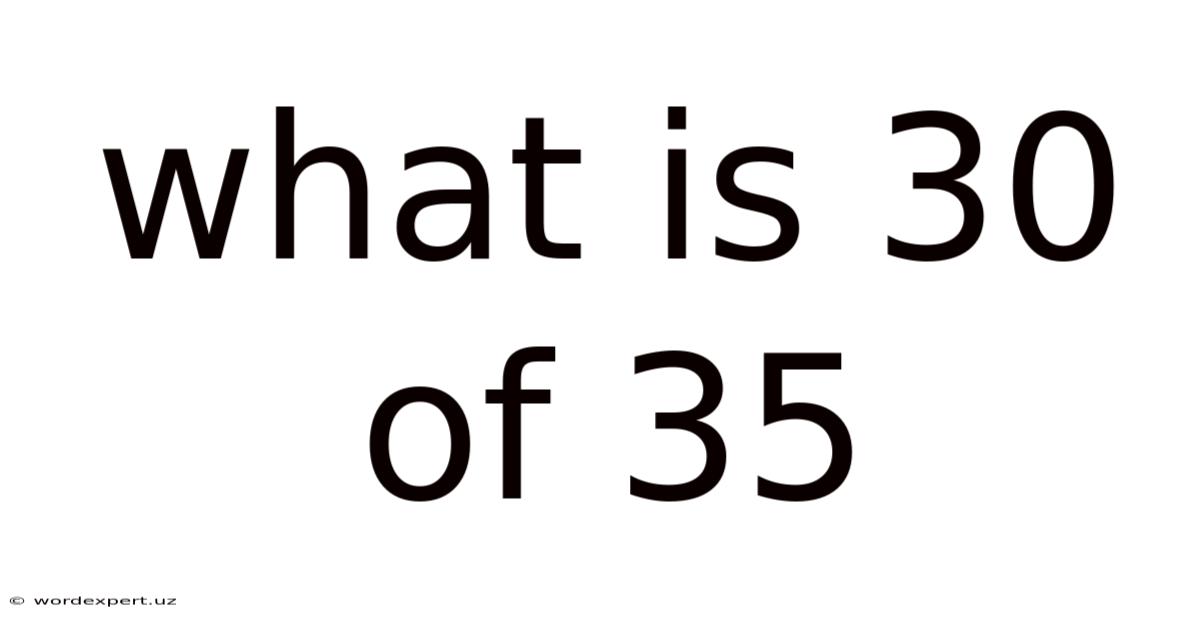
Table of Contents
What is 30 out of 35? Understanding Fractions, Percentages, and Ratios
This article explores the question "What is 30 out of 35?" in a comprehensive way, moving beyond a simple numerical answer to delve into the underlying mathematical concepts and their practical applications. We'll cover fractions, percentages, decimals, and ratios, demonstrating how to calculate and interpret these values in various contexts. Understanding these concepts is crucial for a wide range of applications, from everyday tasks to more complex academic and professional situations.
Understanding Fractions: The Foundation
The core of the problem "30 out of 35" lies in understanding fractions. A fraction represents a part of a whole. In this case, 30 represents the part and 35 represents the whole. We can express this as a fraction: 30/35.
This fraction represents the portion of 35 that is equal to 30. Before we calculate the percentage or decimal equivalent, let's simplify this fraction. Both 30 and 35 are divisible by 5. Dividing both the numerator (top number) and the denominator (bottom number) by 5, we get:
30 ÷ 5 = 6 35 ÷ 5 = 7
Therefore, the simplified fraction is 6/7. This means that 30 out of 35 is equivalent to 6 out of 7. This simplified fraction is often easier to work with and provides a clearer representation of the proportion.
Calculating the Percentage: Expressing the Proportion
Percentages are a way to express fractions as a portion of 100. To convert the fraction 30/35 (or its simplified form 6/7) into a percentage, we perform the following calculation:
(30/35) * 100% = 85.71% (approximately)
Alternatively, using the simplified fraction:
(6/7) * 100% = 85.71% (approximately)
This tells us that 30 out of 35 represents approximately 85.71% of the whole. The percentage provides a readily understandable representation of the proportion, making it easier to compare and interpret the results in various contexts. The slight discrepancy due to rounding is important to keep in mind, and it's often valuable to keep the original fraction or decimal value for precise calculations.
Decimal Representation: Another Perspective
Decimals provide yet another way to represent the proportion. To convert the fraction 30/35 to a decimal, we simply divide the numerator by the denominator:
30 ÷ 35 ≈ 0.8571
This decimal, 0.8571, is equivalent to the percentage 85.71%. Decimals are often useful for calculations involving other decimal numbers or when precision is paramount. In many scenarios, you will round this to 0.86 for simplified calculations.
Ratios: Comparing Quantities
Ratios provide a different perspective on the relationship between 30 and 35. A ratio expresses the relative size of two quantities. In this case, the ratio of 30 to 35 can be written as:
30:35
This ratio can be simplified in the same way as a fraction:
6:7
This means that for every 6 units of one quantity, there are 7 units of the other quantity. Ratios are commonly used to express proportions in various contexts, such as comparing the number of items in different categories or specifying mixtures in recipes.
Practical Applications: Real-World Examples
The concepts of fractions, percentages, decimals, and ratios are essential tools in countless real-world situations. Consider these examples:
-
Academic Performance: If a student answered 30 questions correctly out of 35, their score is 85.71%. This provides a clear indication of their performance.
-
Sales and Marketing: If a company sold 30 units of a product out of a total of 35 units produced, their sales represent 85.71% of the production. This information can be used to assess the success of sales efforts.
-
Finance and Investment: If an investment of $35 yielded a return of $30, the return on investment (ROI) is 85.71%. This helps in evaluating the profitability of the investment.
-
Recipe Scaling: If a recipe calls for a 30:35 ratio of flour to sugar, you can scale it proportionally to any desired quantity.
-
Engineering and Construction: Ratio and proportion are fundamental in scale drawings and precise measurements. A 6:7 ratio might be present in a model scaled down from a real object.
Beyond the Basics: Further Exploration
While we've addressed the core question of "What is 30 out of 35?", this is only the starting point for a deeper understanding of mathematical proportions. Further exploration might involve:
-
Working with more complex fractions: Understanding how to handle fractions with larger numbers or mixed numbers.
-
Applying percentages to real-world problems: Solving problems involving percentage increases, decreases, and discounts.
-
Advanced ratio concepts: Exploring inverse ratios, compound ratios, and their applications.
-
Statistical interpretations: This proportion could be part of a larger dataset, requiring a wider statistical analysis.
Frequently Asked Questions (FAQs)
-
Q: Can I express 30 out of 35 as a mixed number?
A: No, a mixed number is a combination of a whole number and a proper fraction. Since 30 is less than 35, 30/35 is a proper fraction which simplifies to 6/7.
-
Q: Is there a way to calculate this without a calculator?
A: Yes, you can simplify the fraction 30/35 manually by finding the greatest common divisor (GCD) of 30 and 35, which is 5. Then divide both numerator and denominator by 5. To calculate the percentage, you can perform long division to find the decimal value and then multiply by 100.
-
Q: What if the numbers were much larger?
A: With larger numbers, a calculator or computer software will help to efficiently calculate and simplify the fraction to its decimal or percentage form. The fundamental principles remain the same.
-
Q: Why is simplification of fractions important?
A: Simplification makes fractions easier to understand, compare, and use in calculations. It provides a more concise and efficient representation of the proportion.
Conclusion
Understanding "what is 30 out of 35" involves more than just a simple calculation. It necessitates a firm grasp of fundamental mathematical concepts like fractions, percentages, decimals, and ratios. These concepts are interconnected and essential tools applicable across numerous academic, professional, and everyday situations. By mastering these concepts, you build a strong foundation for more advanced mathematical skills and problem-solving abilities. The ability to effortlessly convert between fractions, percentages, and decimals allows for flexibility and efficiency in dealing with proportions and their real-world applications. Remember that while technology can assist, the underlying mathematical understanding remains crucial for effective problem-solving.
Latest Posts
Latest Posts
-
40 Months Is How Long
Sep 15, 2025
-
How Much Time Till 3 15
Sep 15, 2025
-
Child Dose Calculation By Weight
Sep 15, 2025
-
700 Sq Meters To Feet
Sep 15, 2025
-
Copper Wire Price Per Foot
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 35 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.