What Is 30 Of 8
wordexpert
Sep 23, 2025 · 5 min read
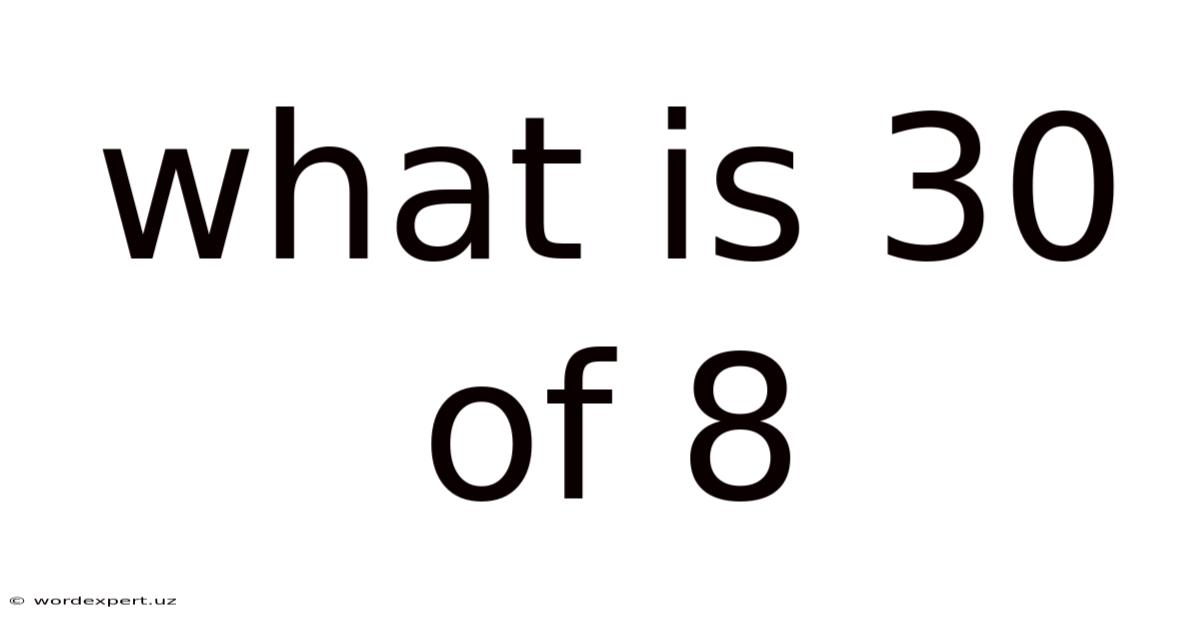
Table of Contents
What is 30% of 8? A Deep Dive into Percentages and Their Applications
Finding 30% of 8 might seem like a simple arithmetic problem, but it opens a door to understanding a fundamental concept in mathematics: percentages. This seemingly basic calculation is crucial in various fields, from everyday budgeting and shopping to complex financial analysis and scientific research. This article will not only show you how to calculate 30% of 8 but will also explore the underlying principles of percentages, different methods for calculating them, and real-world examples to solidify your understanding.
Understanding Percentages: The Foundation
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." So, 30% literally means 30 out of 100, or 30/100, which simplifies to 3/10. Understanding this fraction is key to calculating percentages.
Method 1: Converting Percentage to Decimal
This is the most common and arguably easiest method for calculating percentages. It involves converting the percentage to a decimal and then multiplying it by the number.
Steps:
-
Convert the percentage to a decimal: To convert 30% to a decimal, divide it by 100. This gives you 30/100 = 0.30.
-
Multiply the decimal by the number: Now, multiply the decimal (0.30) by the number you want to find the percentage of, which is 8. Therefore, 0.30 x 8 = 2.4
Therefore, 30% of 8 is 2.4
Method 2: Using Fractions
This method leverages the fractional representation of percentages. As mentioned earlier, 30% is equivalent to 3/10.
Steps:
-
Express the percentage as a fraction: Convert 30% to its fractional equivalent: 30/100. Simplify the fraction by dividing both the numerator and denominator by their greatest common divisor (10): 3/10.
-
Multiply the fraction by the number: Multiply the simplified fraction (3/10) by 8: (3/10) x 8 = 24/10.
-
Simplify the result: Convert the improper fraction 24/10 to a decimal by dividing the numerator by the denominator: 24 ÷ 10 = 2.4
Therefore, 30% of 8 is 2.4
Method 3: Using Proportions
This method utilizes the concept of ratios and proportions to solve for the unknown value.
Steps:
-
Set up a proportion: We can set up a proportion using the relationship between the percentage and the whole number:
30/100 = x/8
where 'x' represents 30% of 8.
-
Solve for x: Cross-multiply to solve for x:
30 * 8 = 100 * x
240 = 100x
x = 240/100
x = 2.4
Therefore, 30% of 8 is 2.4
Real-World Applications of Percentage Calculations
Understanding how to calculate percentages isn't just about solving math problems; it's a crucial skill for navigating everyday life and professional situations. Here are a few examples:
-
Shopping and Sales: Imagine a shirt originally priced at $8 is on sale for 30% off. Knowing that 30% of $8 is $2.40, you can quickly calculate the sale price: $8 - $2.40 = $5.60.
-
Taxes and Tips: Calculating sales tax or service tips involves percentages. If you need to add a 30% tip to an $8 meal, the tip amount would be $2.40.
-
Financial Analysis: Percentages are essential in finance for understanding interest rates, returns on investment, profit margins, and much more. For instance, calculating the growth rate of an investment often involves percentage change calculations.
-
Scientific Research and Data Analysis: Percentages are used extensively in data analysis and scientific research to represent proportions, rates, and changes in various quantities. For example, expressing the percentage of a population exhibiting a certain trait or the percentage increase/decrease in a specific variable.
Beyond the Basics: More Complex Percentage Problems
While calculating 30% of 8 is straightforward, percentage problems can become more complex. Let's explore some variations:
-
Finding the percentage one number is of another: What percentage of 8 is 2.4? To solve this, divide 2.4 by 8 and multiply by 100: (2.4/8) * 100 = 30%.
-
Finding the original number given a percentage and the resulting value: If 30% of a number is 2.4, what is the original number? To solve this, divide 2.4 by 0.30 (the decimal equivalent of 30%): 2.4 / 0.30 = 8.
-
Working with multiple percentages: Calculating consecutive percentage changes or discounts requires careful attention to the order of operations. For instance, finding the final price after two successive 30% discounts is not simply 60% off.
Frequently Asked Questions (FAQs)
-
Q: Can I use a calculator for percentage calculations? A: Absolutely! Calculators are a valuable tool for handling percentage calculations, particularly more complex ones. Most calculators have a percentage function (%) that simplifies the process.
-
Q: What if the percentage is a decimal or fraction? A: Convert the decimal or fraction to a percentage first, then use the same methods outlined above. For example, 0.75 is equivalent to 75%, and 1/4 is equivalent to 25%.
-
Q: Are there any online percentage calculators? A: Yes, many free online percentage calculators are available that can help you quickly perform various percentage calculations.
-
Q: Why are percentages important in real life? A: Percentages provide a standardized and easily understandable way to express proportions and comparisons, making them crucial for various aspects of daily life, finance, and professional fields.
Conclusion: Mastering Percentages for a Brighter Future
Calculating 30% of 8, while seemingly simple, serves as a gateway to understanding a fundamental mathematical concept with wide-ranging applications. By mastering different methods for calculating percentages and understanding their real-world implications, you equip yourself with a valuable skill set for personal and professional success. From everyday budgeting to complex financial decisions, a solid grasp of percentages is a cornerstone of numerical literacy. So, the next time you encounter a percentage problem, remember the methods discussed here, and approach it with confidence. The ability to confidently handle percentages opens doors to more complex mathematical concepts and empowers you to tackle challenges in various aspects of life with greater ease and understanding. Remember, the key is to practice regularly and apply these skills in diverse situations to fully integrate this valuable knowledge.
Latest Posts
Latest Posts
-
What Is 168 25 Simplified Fraction
Sep 23, 2025
-
Biweekly Weeks In A Year
Sep 23, 2025
-
How Long Is 30000 Minutes
Sep 23, 2025
-
Thermal Expansion Of Aluminium Calculator
Sep 23, 2025
-
60 Days From March 7
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.