What Is 4/3 Equal To
wordexpert
Sep 17, 2025 · 5 min read
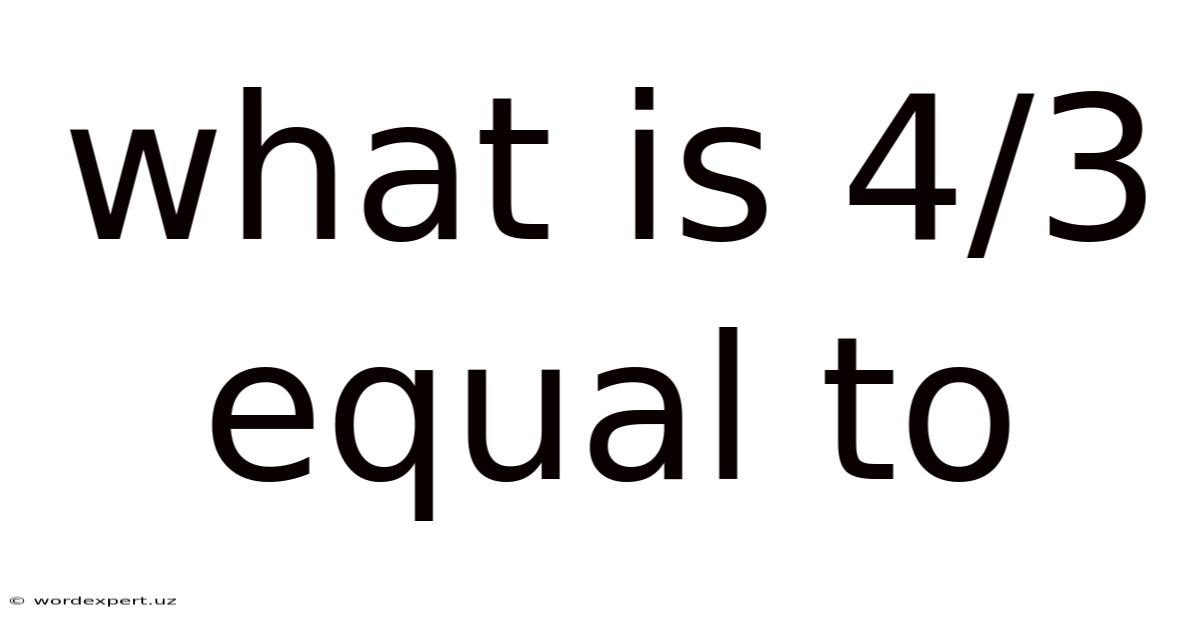
Table of Contents
What is 4/3 Equal To? Unpacking Fractions, Decimals, and Their Applications
Understanding fractions is a fundamental building block in mathematics. This article delves deep into the seemingly simple question: what is 4/3 equal to? We'll explore not only the direct answer but also the broader concepts of fractions, decimals, mixed numbers, and their practical applications in everyday life and various fields. This comprehensive guide will equip you with a solid understanding of this core mathematical concept.
Understanding Fractions: The Basics
Before we tackle 4/3, let's solidify our understanding of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts we are considering.
For example, in the fraction 1/2, the denominator 2 tells us the whole is divided into two equal parts, and the numerator 1 indicates we are considering one of those parts. This represents one-half.
What is 4/3 Equal To? The Direct Answer
The fraction 4/3 represents four parts out of a whole that is divided into three equal parts. Since the numerator is greater than the denominator, this is an improper fraction. An improper fraction is a fraction where the numerator is larger than or equal to the denominator. Improper fractions are greater than or equal to one.
To understand what 4/3 equals, we can express it in a few different ways:
- As a mixed number: A mixed number combines a whole number and a proper fraction (where the numerator is smaller than the denominator). To convert 4/3 to a mixed number, we divide the numerator (4) by the denominator (3).
4 ÷ 3 = 1 with a remainder of 1.
This means 4/3 is equal to 1 1/3. This represents one whole and one-third.
- As a decimal: To convert 4/3 to a decimal, we perform the division:
4 ÷ 3 = 1.333...
The result is a recurring decimal, where the digit 3 repeats infinitely. We often represent this using a bar over the repeating digit: 1.3̅3̅.
Visualizing 4/3
Imagine a pizza cut into three equal slices. The fraction 4/3 represents having four of these slices. You would have one whole pizza (three slices) and one additional slice, hence the 1 1/3 representation. This visual representation makes understanding improper fractions more intuitive.
Working with Improper Fractions and Mixed Numbers: Key Concepts
Understanding how to convert between improper fractions and mixed numbers is crucial for various mathematical operations.
-
Converting an improper fraction to a mixed number: Divide the numerator by the denominator. The quotient is the whole number part of the mixed number. The remainder becomes the numerator of the fractional part, with the denominator remaining the same.
-
Converting a mixed number to an improper fraction: Multiply the whole number by the denominator and add the numerator. This result becomes the new numerator, while the denominator stays the same.
Practical Applications of Fractions: Beyond the Classroom
Fractions aren't just abstract mathematical concepts; they're integral to various aspects of our lives:
-
Cooking and Baking: Recipes frequently use fractions to specify ingredient quantities (e.g., 1/2 cup of flour, 2/3 cup of sugar). Understanding fractions is essential for accurate measurements and successful cooking.
-
Construction and Engineering: Fractions are used in blueprints, measurements, and calculations related to building structures and designing machines. Accuracy is paramount in these fields, making a solid grasp of fractions crucial.
-
Finance and Economics: Fractions are used in calculating interest rates, proportions of investments, and analyzing financial data. Accurate calculations are vital for financial planning and decision-making.
-
Science and Measurement: Fractions are essential in scientific measurements and calculations. In chemistry, for example, fractions are used to represent ratios of elements in compounds.
-
Data Analysis and Statistics: Fractions and ratios are used extensively in analyzing data sets, calculating probabilities, and understanding statistical trends.
Advanced Concepts Related to 4/3
Beyond the basic conversion to mixed numbers and decimals, exploring further mathematical concepts enhances understanding:
-
Rational Numbers: 4/3 is a rational number, which is any number that can be expressed as a fraction of two integers (where the denominator is not zero). All fractions, including improper fractions, are rational numbers.
-
Percentage Representation: To express 4/3 as a percentage, we convert it to a decimal (1.333...) and then multiply by 100: 1.333... × 100 ≈ 133.33%. This shows 4/3 is 133.33% of one whole.
Frequently Asked Questions (FAQ)
Q: What is the difference between a proper and an improper fraction?
A: A proper fraction has a numerator smaller than its denominator (e.g., 1/2, 2/5). An improper fraction has a numerator larger than or equal to its denominator (e.g., 4/3, 5/2).
Q: Why is it important to learn about fractions?
A: Fractions are fundamental to many areas of mathematics and have practical applications in everyday life, including cooking, construction, finance, and science. A strong understanding of fractions is essential for success in various fields.
Q: Can 4/3 be simplified?
A: No, 4/3 is already in its simplest form. The numerator (4) and the denominator (3) don't share any common factors other than 1.
Q: How can I improve my understanding of fractions?
A: Practice is key. Work through various examples, try converting between fractions, mixed numbers, and decimals, and apply your knowledge to real-world problems. Visual aids like diagrams can also be beneficial.
Conclusion: Mastering Fractions, Mastering Opportunities
This in-depth exploration of 4/3 has not only answered the initial question but has also provided a comprehensive overview of fractions, their various representations, and their relevance in diverse fields. Mastering fractions is not just about memorizing rules; it's about developing a conceptual understanding that empowers you to tackle more complex mathematical problems and navigate real-world situations effectively. By practicing and continually applying your knowledge, you'll build a solid foundation in mathematics that opens doors to countless opportunities. Remember that the seemingly simple question "What is 4/3 equal to?" unveils a wealth of mathematical concepts waiting to be explored.
Latest Posts
Latest Posts
-
150 Sq Meters To Feet
Sep 17, 2025
-
Average Height For 14 Year Old Female
Sep 17, 2025
-
Whats A Good Kd Valorant
Sep 17, 2025
-
12 Weeks From August 1
Sep 17, 2025
-
How To Calculate Fev1 Fvc Ratio
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 4/3 Equal To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.