What Is 40 Of 10000
wordexpert
Sep 24, 2025 · 5 min read
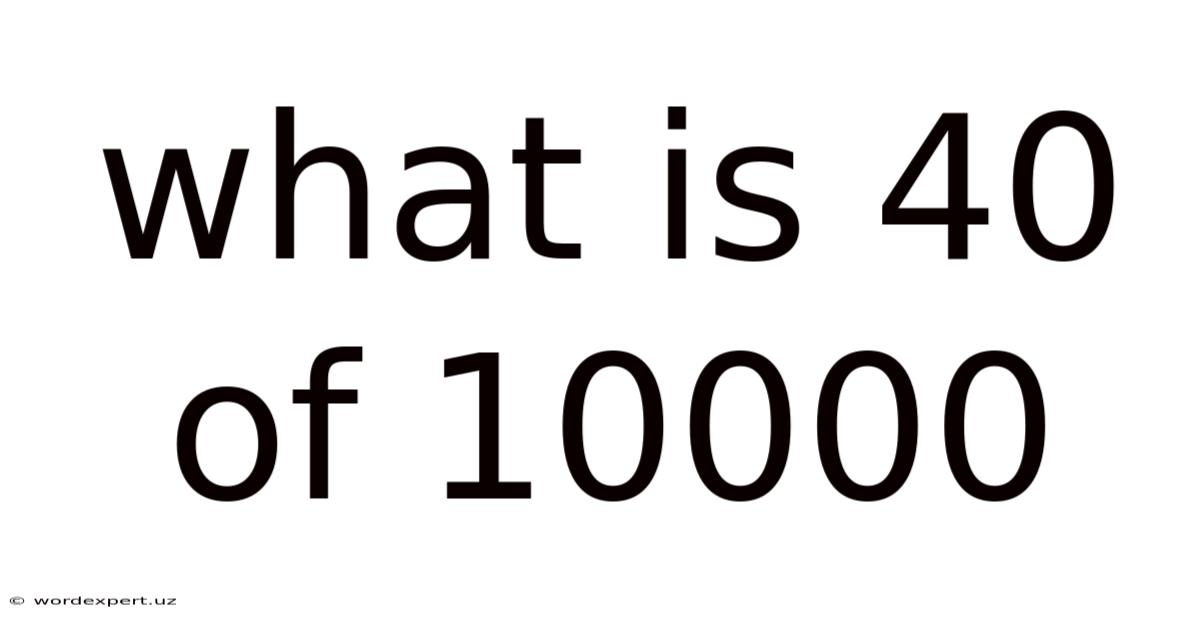
Table of Contents
What is 40 of 10000? Unpacking Percentages and Proportions
Finding out what 40 is out of 10,000 might seem like a simple arithmetic problem, but understanding the underlying concepts of percentages and proportions is crucial for various applications in daily life, from calculating discounts to understanding statistical data. This article will not only provide the answer but also delve deeper into the methods used to solve this and similar problems, enhancing your understanding of fundamental mathematical principles.
Introduction: Understanding the Problem
The core question, "What is 40 of 10000?", essentially asks us to determine the proportion or percentage that 40 represents when compared to the total amount of 10,000. This involves understanding the relationship between parts and wholes, a concept fundamental to many areas like finance, science, and even cooking. We'll explore several ways to calculate this, emphasizing the conceptual understanding behind the mathematical operations.
Method 1: Using Fractions
The simplest approach is to express the relationship as a fraction. 40 out of 10,000 can be written as the fraction 40/10000. To simplify this fraction, we look for common divisors. Both the numerator (40) and the denominator (10000) are divisible by 20:
40 ÷ 20 = 2 10000 ÷ 20 = 500
This simplifies the fraction to 2/500. We can further simplify by dividing both by 2:
2 ÷ 2 = 1 500 ÷ 2 = 250
So, the simplest form of the fraction is 1/250. This means that 40 represents one 250th part of 10,000.
Method 2: Converting to Percentage
Percentages are a common way to express proportions. To convert the fraction 40/10000 to a percentage, we need to express it as a fraction with a denominator of 100. We can do this by dividing both the numerator and denominator by 100:
40/10000 = (40 ÷ 100) / (10000 ÷ 100) = 0.4 / 100
Since percentages represent parts per hundred, we can multiply the decimal 0.4 by 100% to obtain the percentage:
0.4 * 100% = 40%
Therefore, 40 is 0.4% of 10,000. This means that 40 represents 0.4 parts out of every 100 parts of 10,000.
Method 3: Using Decimal Representation
We can also directly express 40 as a decimal fraction of 10,000 by dividing 40 by 10,000:
40 ÷ 10000 = 0.004
This decimal, 0.004, represents the proportion of 40 relative to 10,000. To convert this to a percentage, we multiply by 100%:
0.004 * 100% = 0.4%
This reinforces the result obtained using the fraction method.
Method 4: Applying the Proportion Formula
The proportion formula provides a more general approach to solving such problems. The formula is:
(Part / Whole) = (Percentage / 100)
In our case, the part is 40, and the whole is 10,000. We want to find the percentage:
(40 / 10000) = (x / 100)
To solve for x (the percentage), we can cross-multiply:
40 * 100 = 10000 * x 4000 = 10000x x = 4000 / 10000 x = 0.4
Therefore, x = 0.4%, confirming our previous calculations.
Expanding the Understanding: Applications and Real-World Examples
The seemingly simple problem of finding 40 of 10,000 has wide-ranging applications. Understanding percentage and proportion calculations is essential in:
- Finance: Calculating interest rates, discounts, profit margins, and tax percentages. For example, a 0.4% interest rate on a $10,000 loan would be $40.
- Statistics: Interpreting data, analyzing survey results, and understanding probabilities. For example, if 40 out of 10,000 people surveyed preferred a certain product, it represents a 0.4% preference rate.
- Science: Determining concentrations, ratios, and proportions in experiments and scientific studies. For example, a 0.4% concentration of a specific chemical in a 10,000ml solution indicates 40ml of that chemical.
- Everyday Life: Calculating tips, splitting bills, understanding sale prices, and comparing different offers.
Illustrative Examples:
Let's look at a few more examples to solidify our understanding:
-
Example 1: If a company has 10,000 employees and 120 of them work in the marketing department, what percentage of employees work in marketing? Following the same methods, we find that 120/10000 = 1.2%, meaning 1.2% of the employees work in marketing.
-
Example 2: A store offers a 5% discount on an item priced at $10,000. How much is the discount? Here, 5% of $10,000 is (5/100) * $10,000 = $500.
-
Example 3: If 80 out of 10,000 seeds germinate, what is the germination rate? This is 80/10000 = 0.8%, indicating an 0.8% germination rate.
Frequently Asked Questions (FAQ)
-
Q: What's the difference between a fraction, decimal, and percentage?
- A: They all represent proportions. A fraction shows a part relative to a whole (e.g., 40/10000). A decimal is a fractional representation using base 10 (e.g., 0.004). A percentage expresses the fraction as parts per hundred (e.g., 0.4%).
-
Q: Can I use a calculator to solve these problems?
- A: Yes, a calculator can simplify the calculations, especially for more complex problems. However, understanding the underlying principles is crucial for interpreting the results and applying them in different contexts.
-
Q: What if the numbers are not as easily divisible?
- A: You can still use the same methods. You might need to use a calculator for more precise decimal results. The principles remain the same.
Conclusion: Mastering Proportions and Percentages
Understanding the concept of "what is 40 of 10,000?" extends far beyond a simple arithmetic calculation. It's about grasping the fundamental principles of proportions and percentages – tools essential for navigating various aspects of life. By mastering these concepts, you equip yourself with the skills to analyze data, make informed decisions, and solve a wide array of problems involving relative quantities. Whether dealing with financial transactions, statistical analysis, or everyday scenarios, a strong understanding of proportions and percentages is invaluable. Remember, practice is key to solidifying your understanding and building confidence in applying these crucial mathematical concepts.
Latest Posts
Latest Posts
-
Average Part Time Job Salary
Sep 24, 2025
-
Calories Burned On Stair Stepper
Sep 24, 2025
-
Dnd 5e Figure Out Health
Sep 24, 2025
-
What Is 30 Of 80000
Sep 24, 2025
-
How Many Steps Is 10km
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about What Is 40 Of 10000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.