What Is 40 Of 12
wordexpert
Sep 20, 2025 · 5 min read
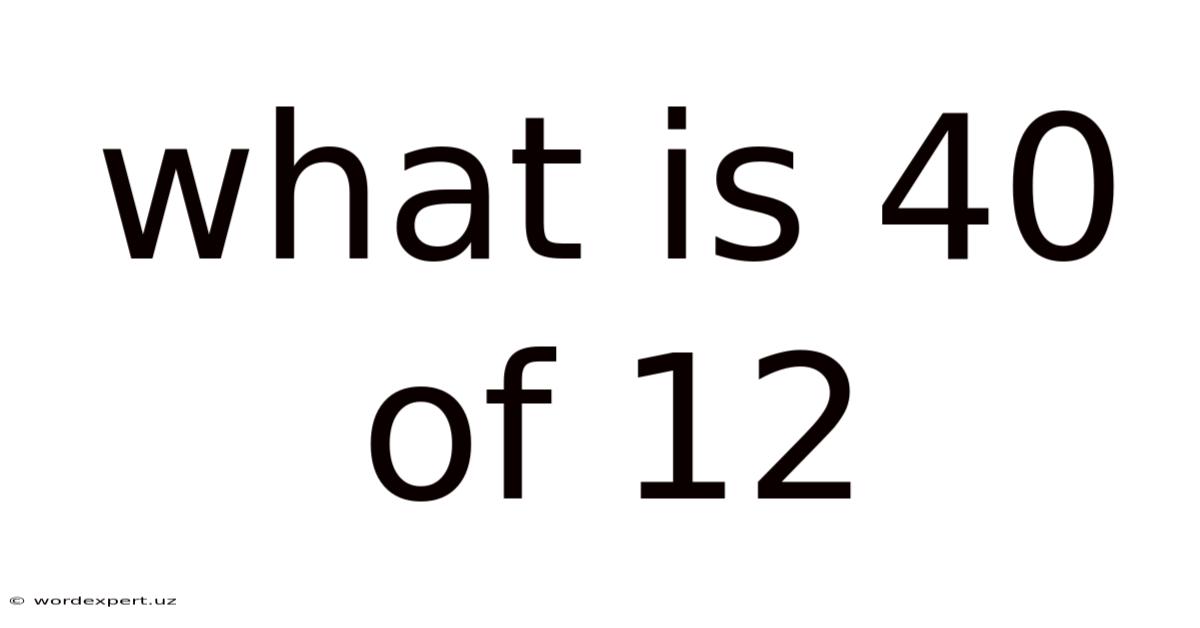
Table of Contents
What is 40% of 12? A Comprehensive Guide to Percentages and Their Applications
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and sales tax to analyzing data and understanding financial reports. This article will thoroughly explore how to calculate 40% of 12, providing a step-by-step explanation, exploring different methods, and delving into the broader concept of percentages and their significance. By the end, you'll not only know the answer but also possess a deeper understanding of percentage calculations and their practical uses.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 40% means 40 out of 100, which can be written as the fraction 40/100 or the decimal 0.40. Percentages are used to represent proportions or parts of a whole.
Method 1: Converting Percentage to a Decimal
This is arguably the most straightforward method for calculating percentages. We convert the percentage into its decimal equivalent and then multiply it by the given number.
Steps:
-
Convert the percentage to a decimal: To convert 40% to a decimal, divide it by 100: 40% ÷ 100 = 0.40
-
Multiply the decimal by the number: Now, multiply the decimal (0.40) by the number you want to find the percentage of (12): 0.40 x 12 = 4.8
Therefore, 40% of 12 is 4.8.
Method 2: Using Fractions
Percentages can also be expressed as fractions. This method provides a different perspective and can be helpful in understanding the underlying mathematical concept.
Steps:
-
Express the percentage as a fraction: 40% can be written as the fraction 40/100.
-
Simplify the fraction (if possible): The fraction 40/100 can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 20: 40/100 = 2/5
-
Multiply the simplified fraction by the number: Now, multiply the simplified fraction (2/5) by 12: (2/5) x 12 = 24/5
-
Convert the improper fraction to a decimal: To get the decimal value, divide the numerator (24) by the denominator (5): 24 ÷ 5 = 4.8
Again, we arrive at the answer: 40% of 12 is 4.8.
Method 3: Proportion Method
This method uses the concept of proportions to solve the percentage problem. This method is particularly useful for visualizing the relationship between the percentage, the part, and the whole.
Steps:
-
Set up a proportion: We can set up a proportion as follows: x/12 = 40/100, where 'x' represents the unknown value (40% of 12).
-
Cross-multiply: Cross-multiply the terms: 100x = 40 x 12
-
Solve for x: Simplify the equation: 100x = 480. Then, divide both sides by 100: x = 480/100 = 4.8
Therefore, 40% of 12 is 4.8.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios:
-
Retail and Sales: Calculating discounts, sales tax, and final prices after applying discounts. For example, a 40% discount on a $12 item would mean a discount of $4.80, resulting in a final price of $7.20.
-
Finance: Determining interest rates, calculating loan payments, analyzing investment returns, and understanding profit margins. Understanding percentages is essential for making informed financial decisions.
-
Data Analysis: Representing data as percentages helps in visualizing and comparing proportions, making it easier to understand trends and patterns. Percentages are frequently used in charts and graphs to represent data effectively.
-
Science and Engineering: Percentages are used in various scientific and engineering calculations, including expressing concentrations, efficiencies, and error margins.
-
Everyday Life: Calculating tips in restaurants, understanding nutritional information on food labels, and interpreting statistics in news reports all involve percentage calculations.
Beyond the Basics: More Complex Percentage Problems
While calculating 40% of 12 is relatively straightforward, understanding percentages extends to more complex scenarios:
-
Finding the percentage: If you know the part and the whole, you can calculate the percentage. For example, if 4.8 is 40% of a number, what is that number? This involves setting up a proportion and solving for the unknown.
-
Finding the whole: If you know the part and the percentage, you can calculate the whole. For instance, if 4.8 represents 40% of a total, what is the total amount? This also requires setting up a proportion and solving for the unknown.
-
Percentage increase/decrease: Calculating the percentage increase or decrease between two values. For example, if a value increases from 10 to 12, the percentage increase is calculated as [(12-10)/10] x 100% = 20%.
-
Compound interest: Calculating the final value of an investment after interest is compounded over time. This involves applying percentage calculations repeatedly.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate percentages?
A: The easiest method is usually converting the percentage to a decimal and then multiplying by the number.
Q: Why are percentages important?
A: Percentages provide a standardized way to compare proportions and parts of a whole, making data easier to understand and interpret across various contexts.
Q: Can I use a calculator to calculate percentages?
A: Yes, most calculators have a percentage function (%) that simplifies the calculation. You can also use the standard multiplication function after converting the percentage to a decimal.
Q: What if the percentage is not a whole number (e.g., 37.5%)?
A: You can use the same methods outlined above. Convert the percentage to a decimal (37.5% = 0.375) and multiply it by the number.
Q: Are there any online tools for calculating percentages?
A: Yes, numerous online percentage calculators are available. These tools can be helpful for quick calculations and checking your work.
Conclusion
Calculating 40% of 12, which equals 4.8, is a simple yet fundamental percentage calculation. This article has provided various methods for solving this problem and explored the broader context of percentages and their applications. Mastering percentage calculations is an essential skill that will benefit you in numerous academic, professional, and everyday situations. Remember, the key is understanding the underlying principles and choosing the method that works best for you. With practice, you'll become proficient in tackling more complex percentage problems and confidently applying this valuable mathematical skill.
Latest Posts
Latest Posts
-
G Force In Car Accident
Sep 20, 2025
-
Cap Rate Calculation Real Estate
Sep 20, 2025
-
How Long Until 930 Am
Sep 20, 2025
-
60 Days From 11 8
Sep 20, 2025
-
Pounds And Ounces Calculator App
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Is 40 Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.